Геометрия в нашем доме: Проект по математике «Геометрические фигуры в моем доме»

Содержание

Проект по математике «Геометрические фигуры в моем доме»

Муниципальное бюджетное общеобразовательное учреждение Покровская средняя школа

Ухоловского муниципального района Рязанской области 391923,Рязанская область, Ухоловский район, с. Покровское, ул. Школьная, д. 19, тел. 5 -54-10

Тема:

Выполнила ученица 6 класса Воронкова Татьяна

Руководитель: учитель математики Воронкова М.И.

Цели и задачи проекта

Цель

· Создать галерею образов геометрических фигур в моем доме.

Задачи работы

1. Изучить теоретические сведения о науке геометрии.

2. Выделить основные геометрические фигуры.

3. Выяснить происхождение геометрических фигур.

4. Изучить сведения о плоских фигурах и объемных.

5. Провести исследование объектов с целью определения их геометрической формы.

Содержание

Введение

Глава 1. Происхождение геометрии.

1.1 Как возникла геометрия?

1.2 Что изучает геометрия?

1.3 Происхождение геометрических фигур.

Глава 2. Организация исследования.

2.1 Исследование объектов.

2.2 Выбор геометрических форм человеком в повседневной жизни.

2.3 Отличие плоских и объемных геометрических фигур.

2.4 Геометрические фигуры в природе.

Глава 3. Практическая часть.

3.1 Составление дневника наблюдений.

Заключение, выводы

Список использованной литературы

Введение

Каждый замечал как много фигур вокруг. Люди давно заинтересовались их разнообразием, строением и свойствами. Мне тоже стало интересно происхождение геометрических фигур: почему фигуры получили такие названия, где и когда они впервые появились. Еще я заметила, что окружающие нас предметы, похожи на геометрические фигуры. И я решила найти ответы на свои вопросы.

Как возникла геометрия?

Геометрия – одна из древнейших наук. Геометрия (греч. geometria, от geо — Земля и metreo — мерю), раздел математики, изучающий пространственные отношения и формы. Происхождение термина «Геометрия», что буквально означает «землемерие», можно объяснить следующими словами, древнегреческого учёного Евдема Родосского (4 в. до н. э.): «Геометрия была открыта египтянами и возникла при измерении Земли. Это измерение было им необходимо вследствие разлития реки Нила, постоянно смывавшего границы». Она зародилась в Древнем Египте.

В этом государстве плодородные земли были расположены на очень узком участке земли – в долине реки Нил. Каждую весну Нил разливался и удобрял землю плодородным илом. Но при разливе реки смывались границы участков, менялись их площади. Тогда пострадавшие обращались к фараону, он посылал землемеров, чтобы восстановить границы участков, выяснить, как изменилась их площадь и установить размер налога. Восстанавливали границы участков особые чиновники – гарпедонапты — натягиватели верёвок.

Уже у древних греков геометрия означала математическую науку, в то время как для науки об измерении Земли был введён термин геодезия. Судя по сохранившимся отрывкам древнеегипетских сочинений, геометрия развилась не только из измерений Земли, но также из измерений объёмов и поверхностей при земляных и строительных работах.

Ремесленникам необходимо было изготавливать посуду, строителям — подбирать камни различной формы для строительства храмов и пирамид, астрономам – измерять углы для определения положения звезд.

Знания постепенно накапливались и систематизировались. Так около

4 тыс. лет назад возникла наука об измерении расстояний, площадей и

объемов, о свойствах различных фигур – геометрия.

Что изучает геометрия?

В геометрии изучаются формы, размеры, взаимное расположение предметов независимо от их других свойств: массы, цвета и так далее. Если взять во внимание только форму и размеры предметов, мы приходим к понятию геометрической фигуры.

Происхождение геометрических фигур

Название «фигура» происходит от латинского слова figura, означающего «внешний вид», «образ». Почти все названия геометрических фигур греческого происхождения, как и само слово геометрия. Однако эти слова вошли в русский язык не непосредственно с греческого, а через латинский язык.

Точка, прямая, плоскость.

А простейшими в геометрии являются три фигуры: — точка, прямая, плоскость. Конечно, самая главная – это точка. Древнегреческий геометр Евклид говорил, что «точка – это то, что не имеет частей». Слово точка по латыни означает результат мгновенного касания, укол. Так, точкой является отверстие, оставленное иглой в листе бумаги. Точка – в русском языке означало конец заточенного гусиного пера. Линия – льняная нить. Луч света также представляет собой модель прямой линии. Натянутая линия – также модель прямой. Плоскость — поверхность.

Все предметы в моем доме напоминают различные геометрические фигуры. Рассмотрим и опишем некоторые из них.

Квадрат

Термин образовался как буквальный перевод соответствующего греческого слова «квадратус» — «четырехугольный».

КВАДРАТ – это прямоугольник, у которого все стороны равны.

Прямоугольник

Термин образован путем соединения двух слов: «прямой» и «угол».

Прямоугольник— это четырехугольник, у которого все углы прямые.

Треугольник

Треугольник— это многоугольник с тремя сторонами.

Термин образован путем соединения двух слов: «три» и «угол». Слово «три» общеславянское, индоевропейского характера.

Круг

Общеславянское слово, имеющее соответствия в германских языках: в древнегерманском «кригер» — «кольцо», «круг», в греческом — «колесо», «круг»).

Круг— это множество всех точек плоскости, расстояние от каждой из которой до данной точки этой плоскости не больше данного расстояния.

Окружность

В переводе с греческого это слово означает «периферия».

Окружность — это множество точек плоскости, находящихся на данном расстоянии от данной точки, лежащей в той же плоскости и называемой ее центром. Окружность — это граница круга.

Овал

Французское слово «оваль» — «овальный» произошло от латинского «овум» — «яйцо». Овал — замкнутая выпуклая гладкая плоская кривая.

Ромб

Одни считают, что этот термин произошел от греческого слова «ромбос», означающего »бубен», т. к. ромб похож на четырехугольный бубен, другие — что от греческого слова «ромб», которое означает «вращающееся тело», «веретено», т.к. сечение в обмотанном веретене имеет форму ромба.

Трапеция

Греческое слово «трапедзион» переводится как «столик» (сравним со словом «трапеза»). Трапеция — это выпуклый четырехугольник, у которого две противоположные стороны параллельны, а две другие не параллельны.

Куб

Термин «куб» происходит от греческого слова в переводе означающего — «игральная кость». Она имела форму кубика, и название это перешло на любое тело той же формы. Этот термин впервые встречался у пифагорейцев (VI-IV вв. дон. э.).

Параллелепипед

Термин образован путем соединения двух греческих слов: «параллелос» — «параллельный» и «эпипедос» — «плоскость».

Параллелепипед — призма, основанием котopoй является параллелограмм.

Конус

Конус — от греческого слова «конос» (сосновая шишка, остроконечная верхушка шлема).

Пирамида

Пирамида — от греческого слова «пюрамис», которым греки называли египетские пирамиды. А это слово происходит от древнеегипетского слова «пурама», которым эти пирамиды называли сами египтяне.

Призма

Призма — от слова «присма» («опиленная», «отпиленная часть»).

Цилиндр

Цилиндр — от латинского слова «цилиндрус» (валик, каток).

Сфера

СФЕРА – латинская форма греческого слова «сфайр» — мяч.

Таким образом, названия геометрических фигур первоначально были названием конкретных предметов, имеющих форму более или менее близкую к форме фигуры.

Чем же отличаются плоские и объёмные фигуры?

Плоские можно целиком расположить на одной плоской поверхности.

Объемные фигуры занимают определённое пространство, возвышаются над плоской поверхностью.

Геометрические фигуры в природе

Ученые придерживаются мнения о том, что все, что создается человеком, создается на основе наблюдений за окружающей человека природой. Значит и геометрические фигуры нужно искать в природе. Посмотрите вокруг. Многие окружающие нас предметы напоминают геометрические фигуры.

Вокруг нас находится большое количество предметов, имеющих форму геометрических фигур. Углы, отрезки и плоскости являются объектами искусственного происхождения и изготовлены человеком. Предметы природного происхождения имеют округлые формы, такие как шар, эллипс, дуга. Исключение составляют кристаллы, которые имеют прямоугольные формы.

Дневник наблюдений:

Проблемный вопрос	Предмет	Фигуры, из которых состоит предмет
геометрия на кухне	Холодильник	Прямоугольный параллелепипед
	Кастрюля	Цилиндр
	Тарелка	Круг, окружность
	Микроволновая печь	Прямоугольный параллелепипед
	Кухонный шкаф	Прямоугольный параллелепипед
геометрия в спальне	Шкаф	Прямоугольный параллелепипед
	Кровать	Прямоугольный параллелепипед
	Компьютер	Прямоугольник
	Стол	Прямоугольник
геометрия в холодильнике	Банка сгущенки	Цилиндр
	Банка молока	Цилиндр
	Колбаса	Цилиндр
	Сыр	Круг, круговой сектор
	Банка йогурта	Усеченный конус
	Пачка масла	Прямоугольный параллелепипед
геометрия на улице	Дом	Прямоугольный параллелепипед
	Столб, столбы	Цилиндр, параллельные прямые
	Баня	Прямоугольный параллелепипед
	Провода электрические	Параллельные прямые
	Дорога	Кривая линия
	Фонарь	Овал
геометрия на огороде и в саду	Морковь	Конус
	Бочка	Цилиндр
	Теплица	Прямоугольный параллелепипед
	Капуста	Шар
	Грядка	Прямоугольный параллелепипед
	Ведро	Усеченный конус
	Лейка	Цилиндр
геометрия жилища	Крыша	Пирамида, угол
	Дом	Прямоугольный параллелепипед
	Дверь	Прямоугольник
	Окна	Прямоугольник

ЗАКЛЮЧЕНИЕ

Простейшие геометрические фигуры, такие как круг, треугольник, прямоугольник являются именно теми фигурами, с которыми человек познакомился в глубокой древности. Свойства этих фигур первыми пришли на помощь человеку, так как эти фигуры всегда имели широкое применение в практической жизни.

Итак, после проведенной исследовательской работы я могу сделать выводы о наиболее полезных свойствах геометрических фигур:

Окружность и круг – это удивительно гармоничные фигуры. Окружность – единственная кривая, которая может “скользить сама по себе”, вращаясь вокруг центра.

Круг – это колесо. Колесо – это прогресс – движение вперед. Если остановится колесо, то остановится колесо Истории. Все движется по кругу.

Треугольник — единственная геометрическая фигура, которая обладает свойством жёсткости. Треугольник всегда имел широкое применение в практической жизни. Так, в строительном искусстве испокон веков используется свойство жесткости треугольника для укрепления различных строений и их деталей.

Квадрат служит эталоном при измерении площадей всех фигур. Зная о многоугольниках и их видах, можно создать очень красивые предметы украшения, построить разнообразные и уникальные здания.

Человеческие представления о красивом, формируются под влиянием того, что человек видит в живой природе. В различных своих творениях, очень далёких друг от друга, она может использовать одни и те же принципы.

И я могу сказать, что геометрические фигуры создают красоту в искусстве, архитектуре, природе, в окружении человека. Красота – всюду. Есть она и в науке, и в особенности в её жемчужине – математике.

Литература

1. Клепа. Альманах. №46, 1998г.

2. Минковский В.Л. За страницами учебника математики. М.: Просвещение, 1966

3. http://www.kakprosto.ru/kak-807590-kak-voznikla-geometriya#ixzz3ZwNH0Hxi

4. dic.academic.ru›Геометрия

5. images.yandex.ru›картинки геометрических фигур

6. ru.wikipedia.org›Категория:Геометрические фигуры

7. Математика 6 класс. Учебник для образовательных учреждений. М.: Мнемозина, 2014

8. Энциклопедия для детей. Математика. Сост. М. Аксенова – М. : Аванта +, 2004

9. Депман И.Я., Виленкин Н.Я. “За страницами учебника математики” Дрофа 2003

10. Дорохов А.А., Михайлов М.М., Куценко Г.М., Назаров А.А. “Что такое? Кто такой?” Дрофа 2005

Геометрия в жизни человека

Авторы
Руководители
Файлы работы
Наградные документы

Енюкова Ю.С. 1

1ГБОУ гимназия им.С.В.Байменова города Похвистнево

Антонова Г.В. 1

1ГБОУ гимназия имени С.В. Байменова города Похвистнево Самарской области

Автор работы награжден дипломом победителя III степени

Диплом школьникаСвидетельство руководителя

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

1.Введение

«Если бы геометрия так же противоречила

нашим страстям и интересам, как нравственность,

то мы бы так же спорили против нее

и нарушали ее вопреки всем доказательствам»

Готфрид Вильгельм Лейбниц

Актуальность: В прошлом учебном году я начала изучать предмет геометрию и, по мнению многих учащихся (провела опрос учащихся седьмых классов), он является одним из сложных школьных предметов. Многие, 81% из опрошенных учащихся, не совсем понимают, а зачастую и не знают практического значения геометрии в жизни. Я также не совсем понимала необходимость изучения предмета геометрия.

Проблема: Для чего мы изучаем геометрию, где можно применить полученные знания, как часто приходится сталкиваться с геометрическими фигурами? Встречается ли где-нибудь информация, связанная с геометрией, кроме уроков математики?

Гипотеза: Если человечество на протяжении многих веков приобретало всё новые и новые знания по геометрии, то где эти знания применяются и используются.

Объект: геометрия.

Предмет: использование геометрии вне школы.

Цель: найти доказательство практической значимости геометрии в жизни человека.

Задачи:

Изучить историю возникновения геометрии.

Познакомиться с профессиями, которые напрямую связаны с геометрией.

Узнать, чем может помочь геометрия на практике.

Провести анализ полученных результатов.

Теоретическая значимость

Геометрия — раздел математики, изучающий пространственные отношения и формы, а также другие отношения и формы, сходные с пространственными по своей структуре. Слово геометрия — греческое, в переводе на русский язык означает землемерие. Такое название связано с применением геометрии для измерений на местности. Геометрия в первоначальном значении есть наука о фигурах, взаимном расположении и размерах их частей, а также о преобразованиях фигур. Это определение вполне согласуется с определением геометрии как науки о пространственных формах и отношениях. Действительно, фигура, как она рассматривается в геометрии, и есть пространственная форма.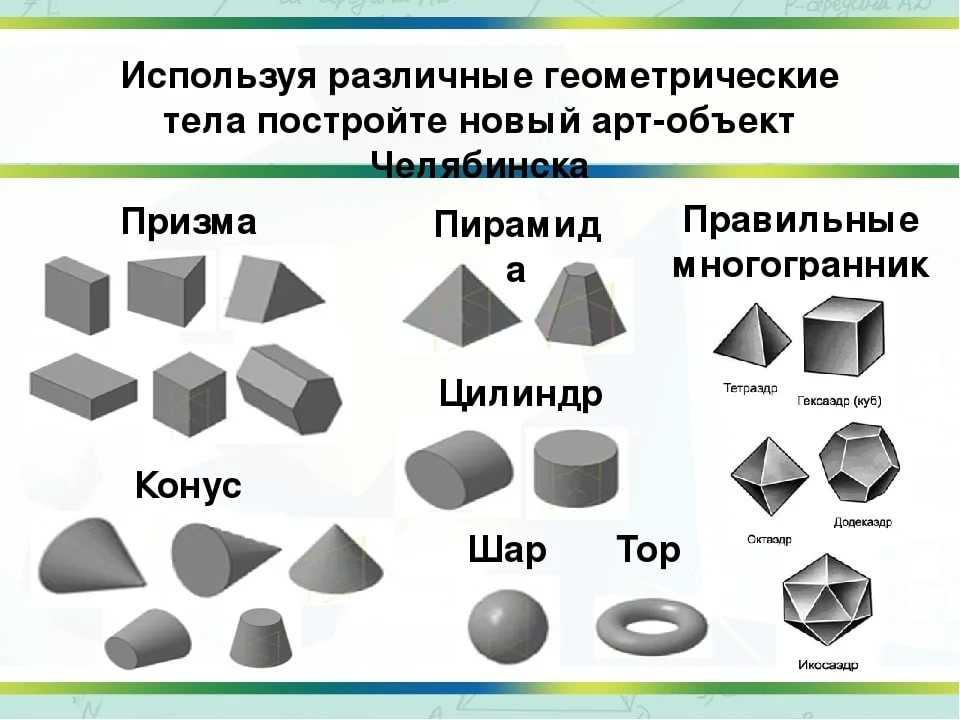 Поэтому в геометрии говорят, например, шар, а не тело шарообразной формы. Расположение и размеры определяются пространственными отношениями. Наконец, преобразование, как его понимают в геометрии, также есть некоторое отношение между двумя фигурами — данной и той, в которую она преобразуется.

1.1. Историческая справка

Геометрия возникла давно, это одна из самых древних наук. Геометрия (от греч. ge — земля и metrein — измерять)— наука о пространстве, точнее — наука о формах, размерах и границах тех частей пространства, которые в нем занимают вещественные тела. Таково классическое определение геометрии, или, вернее, таково действительное значение классической геометрии. Однако современная геометрия во многих своих дисциплинах выходит далеко за пределы этого определения. Развитие геометрии принесло с собой глубоко идущую эволюцию понятия о пространстве. В том значении, в котором пространство как математический термин широко употребляется современными геометрами, оно уже не может служить первичным понятием, на котором покоится определение геометрии, а, напротив, само находит себе определение в ходе развития геометрических идей. Важную роль играли и эстетические потребности людей: желание украсить свои жилища и одежду, рисовать картины окружающей жизни. Все это способствовало формированию и накоплению геометрических сведений. За несколько столетий до нашей эры в Вавилоне, Китае, Египте и Греции уже существовали начальные геометрические знания, которые добывались в основном опытным путем. Но они не были еще систематизированы и передавались от поколения к поколению в виде правил и рецептов, например, правил нахождения площадей фигур, объемов тел, построение прямых углов и т.д. Не было еще доказательств этих правил, и их изложение не представляло собой научной теории. Геометрия дает общее понятие о геометрической фигуре, под которой понимают не только тело, поверхность, линию или точку, но и любую их совокупность. Геометрия в первоначальном значении есть наука о фигурах, взаимном расположении и размерах их частей, а также о преобразованиях фигур. Это определение вполне согласуется с определением геометрии как науки о пространственных формах и отношениях. Действительно, фигура и есть пространственная форма; поэтому в геометрии, например, говорят, «шар», а не «тело шарообразной формы». Расположение и размеры определяются пространственными отношениями; наконец, преобразование, как его понимают в геометрии, так же есть некоторое отношение между двумя фигурами — данной и той, в которую она преобразуется.

1.2. Геометрия в 21 веке

Посмотрите вокруг — всюду геометрия! Современные здания и космические станции, подводные лодки, интерьеры квартир — всё имеет геометрическую форму. Геометрические знания являются сегодня профессионально значимыми для многих современных специальностей: для дизайнеров и конструкторов, для рабочих и учёных. И уже этого достаточно, чтобы ответить на вопрос: «Нужно ли нам геометрия?»

Недостаток жизненного опыта позволяет некоторым школьникам и даже студентам думать, что больше половины изучаемых предметов абсолютно бесполезны и никогда не пригодятся в жизни. На самом деле, знания могут прийти на помощь в неожиданный момент, и доставать учебники уже не будет времени. Одна из полезнейших наук — геометрия, некоторые виды деятельности без нее немыслимы.

Без знания геометрии невозможно построить дом или отремонтировать квартиру. Например, при установке стропил на крышу понадобится формула расчета высоты треугольника, особенно, если крыша несимметричная. Без этого нельзя будет рассчитать длину перекладин, а также узнать количество кровельного материала. Чтобы посчитать количество блоков или кирпичей для стены, плиток для ремонта ванной комнаты, досок для пола — необходимы знания формул площади поверхности, а для объемных покрытий, например, утеплителей — формул объема. Для разработки системы вентиляции, обогрева, канализации или водоснабжения в доме или квартире потребуется расчет внутреннего объема труб, а это невозможно сделать без формулы площади круга. Конечно, можно доверить это профессионалам — но без знания геометрии будет невозможно даже разобраться в чертежах и проверить качество работы. Вообще, чертежи встречаются даже далекому от них человеку на протяжении всей жизни. Это чертеж дома или план ремонта, чертежи деталей на заводе, знать которые нужно не только конструктору и технологу, но и токарю, сварщику, контролеру, менеджерам отделов закупок и продаж. С чертежами непременно столкнется автолюбитель, который захочет провести ремонт своей машины.

Геометрия присутствует практически во всех сферах нашей жизни: нас окружают круглые, квадратные, прямоугольные, треугольные, сферические, кубические, цилиндрические, конические и другие объекты.

Обычно мы не задумываемся о том, почему объекты имеют ту или иную форму, а ее выбор далеко не случаен.

Одна из самых распространенных форм – это окружность и то, что ею ограничено, то есть круг. Вы, наверное, не задумывались, почему трубы – круглые в сечении? Одна из причин в том, что окружность – это замкнутая дуга с постоянной шириной. По этой причине, например, люки не проваливаются вниз, что приводило бы к несчастным случаям, а будь они квадратной или прямоугольной формы, это стало бы неизбежным.

Еще одно свойство окружности: из всех замкнутых кривых заданной длины круг покрывает наибольшую площадь. Это объясняет тот факт, что природа часто использует круг и его объемный эквивалент – сферу. Природа всегда останавливает выбор на самых стабильных формах, минимально расходующих энергию.

2.Основная часть

2.1. Профессии, связанные с геометрией

Конечно, математика нужна нам везде: в автобусе, в магазине, дома и в школе. Однако профессии, где нужна только геометрия, не встречаются.

Архитектор

Архитектура – это музыка, застывшая в камне. На мой взгляд, самая “геометрическая профессия” – архитектор. Архитектура — одна из наиболее всеобъемлющих областей человеческой деятельности, занимающаяся организацией пространства и времени и решающая любые пространственные и временные задачи, от разработки стратегий развития агломераций до дизайна дверных ручек. Перед тем как построить жилое здание, проектируют будущую постройку на чертежах в уменьшенном масштабе. Архитектор придумывает основную концепцию здания, его облик, увязывает воедино все нюансы. Задача архитектора — спроектировать сооружение, максимально отвечающее потребностям заказчика.

Инженер

Еще одна немаловажная профессия — инженер. Инженер-строитель — это производитель работ, т.е. прораб, он руководит общестроительными работами, монтажом конструкций, осуществляет контроль над качеством.

В проектных организациях инженеры выполняют работы по комплексному проектированию: архитектурной, конструктивной части (электроснабжение, отопление и вентиляция, водопровод и канализация, слаботочные системы — телефон, пожарная сигнализация, теленаблюдение и др. ). Кроме того, разрабатывают генеральные планы проектируемых комплексов, куда входят дороги, земляные работы, организация строительства. Направление деятельности строителей очень широкое — кроме возведения зданий, производственных комплексов, фабрик, они проектируют мосты, гидротехнические сооружения, плотины, дамбы и т. д.

Дизайнер

Дизайн — это творческая деятельность, целью которой является определение формальных качеств изделий промышленности. Эти качества включают и внешние черты изделия, но главным образом те структурные взаимосвязи, которые превращают изделие в единое целое, как с точки зрения потребителя, так и с точки зрения изготовителя. Быть дизайнером это означает быть творческой личностью. Для этого те, кто решил выбрать эту профессию, отправляются на специальные курсы подготовки, куда обязательно будут входить изучение черчения, геометрии и других специальных программ, которые пригодятся будущему специалисту.

Конструктор

Конструктор осуществляет конструкторское и технологическое проектирование, разрабатывает и внедряет инновационные технологические процессы производства, разрабатывает технологические конструкции различного назначения, отдельные их элементы и части, цехи. Проводит исследования в области конструирования с использованием новых разработок, достижений различных областей науки. Для того чтобы стать конструктором, необходимо изучать технику, механику, физику, алгебру, геометрию, химию… И обладать такими качествами как: высокая концентрация и устойчивость внимания, логика, технический склад ума.

Модельер

Модельер — специалист по изготовлению моделей одежды, создатель экспериментальных образцов, определяющий образ и стиль, общее конструктивное решение, изобретающий новые технологические решения и разрабатывающий декор, выбирающий цвет и материалы, продумывающий аксессуары и дополнения. Благодаря работе модельера наши вещи становятся более удобными, стильными и качественными.

Психолог

Наш характер определяется многими признаками, но оказывается, не остается в стороне и геометрия. Когда мы смотрим на какие-либо предметы, то на подсознательном уровне, сопоставляем их с какими-то геометрическими фигурами и стараемся окружить себя такими же.

Существует даже такая наука — психогеометрия. Суть её состоит в исследовании личности. В её основе лежит учение Карла Юнга о психических типах личностей. Однако автором психогеометрии является Сьюзен Деллингер — специалист по социально-психологической подготовке управленческих кадров. Работа С. Деллингер «Психогеометрия: как использовать психогеометрию для воздействия на людей» очень популярна в США. В нашей стране труд С. Деллингер был переработан нашими соотечественниками Анатолием Алексеевым и Ларисой Громовой.

Психогеометрия — это уникальная практическая система анализа личности. Она позволяет:

Мгновенно определить тип личности интересующего вас человека и вашу собственную форму.

Дать подробную характеристику личностных качеств и особенностей поведения любого человека.

Составить сценарий поведения для каждой формы личности в типичных ситуациях.

Чтобы определиться в мире психогеометрии, которая как оказалось, влияет на все наши поступки, Деллингер выявила пять психологических типов, каждому из которых соответствует своя геометрическая фигура: квадрат, круг, треугольник, зигзаг, прямоугольник. Каждая фигура имеет свои психологические особенности и по-разному взаимодействует с остальными. Что ж, заманчиво, не правда ли? Да и не поспоришь ведь, что «круглые» глаза иногда смотрят на мир иначе, чем «квадратные»!

Исследование личности с помощью психогеометрии позволяет быстро и точно нарисовать психологический портрет испытуемого, узнать какие черты его характера являются главными, а какие – второстепенными, а также понять, с кем человеку сложнее всего взаимодействовать.

2.2. Применение геометрии на практике

В школе мы несколько лет подряд прилежно изучаем геометрию. Но не зря ли мы тратим время? Чем может помочь геометрия в жизни? Измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться.

Завариваем чай

Перед вами стеклянные чайники четырёх моделей одинаковой вместимости (рис. 1). В каком чайнике заваренный чай останется тёплым дольше?

Решение. Из курса физики известно, что время охлаждения пропорционально площади поверхности тела. Значит, чем меньше поверхность чайника, тем дольше остывает чай. Самая маленькая площадь поверхности у четвёртого чайника, так как его форма близка к сфере ( ).

Рис. 1

И справление ошибки кроя

Предположим, вам нужно вырезать для аппликации два разносторонних треугольника из цветной бумаги — «левый» и «правый». Вы случайно вырезали их одинаковыми — оба «левые». Можно ли, не используя новый кусок бумаги, исправить ошибку?

Решение. Для исправления ошибки вы можете разрезать один из треугольников, например, так, как показано на рисунке 2, а затем сложить из него нужный треугольник.

Рис. 2

Строим прямой угол на земле

Известен старинный способ построения прямого угла на поверхности земли. Его использовали ещё древние египтяне. Они строили прямой угол с помощью обычной верёвки, на которой через равные расстояния завязаны тринадцать узелков. Чтобы отрезки на верёвке были одинаковые, узелки завязывали вокруг колышков, вбитых в землю на равном расстоянии друг от друга. В чём состоит этот «верёвочный» способ?

Решение. В древности при закладке храма такую верёвку с узелками использовали для определения направлений его стен. Концы верёвки на месте крайних узелков связывали, а затем натягивали её на три колышка так, как показано на рис. 3. Стороны при этом имели соотношение 3:4:5. В таком треугольнике один из углов получается прямым. Впоследствии этот факт был доказан в теореме Пифагора. Поэтому первых геометров называли ещё «натягивателями верёвок». Нужно отметить, что таким способом построения прямого угла на местности пользуются и сегодня, например при закладке фундамента небольшого строения.

Рис. 3

Выдерживание прямых углов

Если вы решили склеить коробку, сделать шкатулку или выложить плитку, важно, чтобы все детали были точными прямоугольниками или квадратами. В противном случае всё пойдёт наперекосяк. Как проверить, имеет ли деталь нужную «геометрию»?

Решение. Чтобы проверить, у всех ли деталей, с которыми вы работаете, прямые углы и одинаковые линейные размеры, можно использовать строительный угольник (см. рис.4), а можно применить знания по геометрии. Убедитесь в том, что противоположные стороны четырёхугольника равны и при этом диагонали тоже имеют одинаковую длину. Как вы и сами знаете, сделать это можно с помощью линейки. Но вот вопрос: обязательно ли проверять и стороны, и диагонали? Геометрия утверждает, что да! Например, на рис. 5 диагонали в четырёхугольнике слева равны, но очевидно, что его углы совсем не прямые. А в четырёхугольнике справа противоположные стороны равны, но это тоже не прямоугольник. Для проверки прямоугольности геометрия ещё советует убедиться в равенстве всех четырёх отрезков, на которые разбиваются диагонали в точке их пересечения.

Рис. 5

Рис. 4

Укрепляем калитку

Прямоугольная калитка (рис. 6, слева) со временем расшатывается и становится похожей на параллелограмм. Этого можно избежать, прибив к ней ещё одну планку. Только надо знать, как это сделать.

Решение.

Рис. 6

ыбор такого положения планки, как показано на рис. 6, (справа) основан на свойстве жёсткости треугольника. Оно гласит: существует единственный треугольник с заданными длинами сторон. Планка и есть гипотенуза такого треугольника.

3.Заключение

Метод решения хорош, если с самого начала мы можем предвидеть — и далее подтвердить это, — что, следуя этому методу, мы достигнем цели. Так говорил великий немецкий философ, логик, математик Готфрид Вильгельм Лейбниц. Значение геометрии огромно. Геометрия встречается во многих профессиях, без которых человечество не смогло обойтись. Например, перед тем как построить жилое здание, люди проектируют будущую постройку на чертежах в уменьшенном масштабе. Этим занимается архитектор. Тот, кто руководит общестроительными работами и осуществляет контроль над качеством, называется инженером-строителем. Конструктор разрабатывает элементы, части технологических конструкций. Для того чтобы стать конструктором, необходимо сначала выучить множество наук, среди которых присутствует геометрия. С помощью модельера наши вещи становятся более удобными, стильными и качественными. Его задача изготавливать новые модели одежды, определять общее конструктивное решение, придумывать различные дополнения. Психолог с помощью психогеометрии быстро и точно нарисует психологический портрет испытуемого, узнает, какие черты его характера являются главными, а какие – второстепенными, а также поможет понять, с кем человеку сложнее всего взаимодействовать. А если на минуту представить, что геометрии не существует и ни один человек не подозревает о наличие геометрии, то неужели люди до сих пор жили бы в пещерах, ходили на охоту и одевались в шкуры животных? Изучив литературу, интернет — источники, я сделала вывод, что между геометрией и практической действительностью есть множество точек соприкосновения. Со своим проектом я выступила перед учащимися 7 – 8 классов, большинство учащихся о практическом применении геометрии и не ведало. Поэтому смело можно сделать вывод: если бы люди не стали изучать геометрию и пользоваться ею, то прогресс и множество современных изобретений дались бы человечеству с трудом и возможно гораздо позже.

4.Использованные литература и источники

https://www.nkj.ru/archive/articles/19307/

https://infourok.ru/material.html?mid=137763

https://7lafa.com/pageanswer.php?id=44485

http://obuchonok.ru

https://ru.wikipedia.org/wiki/Геометрия:

http://interesnik.com/geometriya-v-nashej-zhizni/

Геометрия в нашей жизни

https://www.kakprosto.ru/kak-893421-chem-pomozhet-znanie-geometrii-v-

buduschem#ixzz4zda9DK8v

http://enciklopediya1.ru/index/0-397

Просмотров работы: 28667

11 примеров геометрии в повседневной жизни — StudiousGuy

Слово «Геометрия» происходит от греческих слов «Гео» и «Метрон», что означает Земля и Измерение соответственно. В грубом переводе на «Измерение Земли» геометрия в первую очередь связана с характеристиками фигур, а также форм. Практически геометрия играет большую роль в определении площадей, объемов и длин. Евклид считается «отцом геометрии».

С самого рождения людей привлекают разнообразные формы, узоры и цвета. Сказанное может быть подкреплено тем, что при покупке вещей на рынке человека привлекают ткани с завораживающими узорами, книги в привлекательных обложках, солнцезащитные очки нестандартной формы, украшения с завораживающими узорами, чайные кружки. с красивыми формами, и что-нет! Геометрию можно назвать «вездесущей». Более того, геометрические формы различных игрушек играют исключительно важную роль в развитии познавательных навыков у детей на ранних этапах их роста. Давайте обсудим некоторые важные примеры геометрии, которые не упустят ни единого шанса сыграть центральную роль в повседневной жизни людей.

1. Природа

Важнейшим примером геометрии в повседневной жизни является природа, окружающая человека. Если присмотреться, можно обнаружить различные геометрические формы и узоры в листьях, цветах, стеблях, корнях, коре, и этот список можно продолжить. Организация пищеварительной системы человека как трубка внутри трубки также определяет роль геометрии. Листья на деревьях имеют разную форму, размер и симметрию. Разные фрукты и овощи имеют разную геометрическую форму; возьмем, к примеру, апельсин, это сфера, и после очистки можно заметить, что отдельные дольки образуют идеальную сферу.

Присмотревшись к сотам, можно увидеть шестиугольные узоры, расположенные тандемно. Точно так же, рассматривая снежинку под микроскопом, исследователь может стать гостем красивых геометрических узоров.

Следующий интересный пример роли геометрии в природе образован паттерном, широко известным как «Шесть вокруг одного». Цветы демонстрируют узоры «шесть вокруг одного», также называемые «самой плотной упаковкой кругов», «шестиугольной упаковкой» и «мозаичными шестиугольниками».

2. Технологии

Наиболее распространенным примером геометрии в повседневной жизни являются технологии. Будь то робототехника, компьютеры или видеоигры, геометрия применяется практически ко всем основополагающим понятиям. Программисты могут работать, потому что понятия геометрии всегда в их распоряжении. Виртуальный мир видеоигр создается только потому, что геометрические вычисления помогают в разработке сложной графики видеоигр. Raycasting, процесс съемки, использует двухмерную карту для стимуляции трехмерного мира видеоигр. Raycasting помогает увеличить объем обработки, поскольку расчеты выполняются для вертикальных линий на экране.

3. Дома

Геометрия не оставляет ни единого шанса сыграть значительную роль и в домах. Окна, двери, кровати, стулья, столы, телевизор, коврики, ковры, подушки и т. д. имеют различную форму. Кроме того, на простынях, стеганых одеялах, покрывалах, циновках и коврах есть различные геометрические узоры.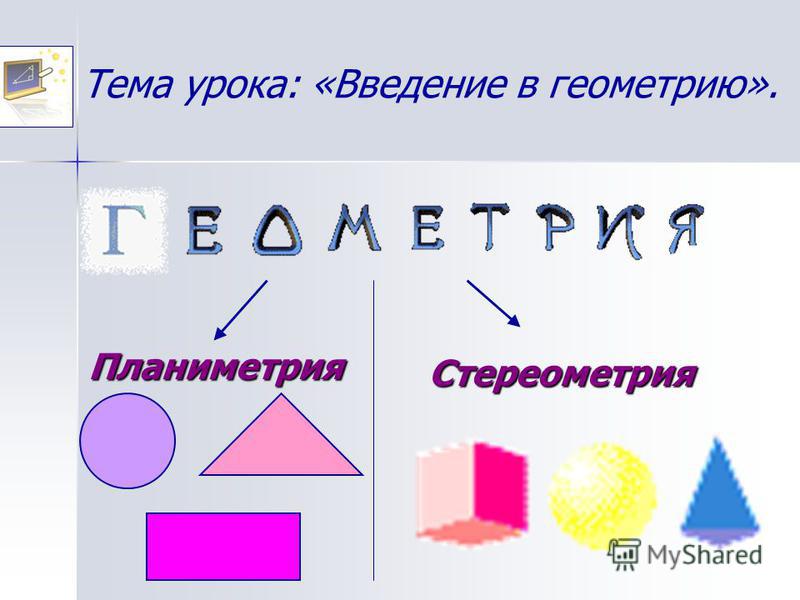 Геометрия также важна для приготовления пищи. Шеф-повар должен добавить все ингредиенты в точных пропорциях и соотношениях, чтобы приготовить вкусное блюдо. Кроме того, при организации комнаты каждое пространство используется, чтобы сделать комнату более привлекательной. Придают дому более презентабельный вид с помощью ваз, картин и различных декоративных предметов, которые имеют разную геометрическую форму и на них нанесены разные узоры.

4. Архитектура

Строительство различных зданий или памятников тесно связано с геометрией. Прежде чем строить архитектурные формы, математика и геометрия помогают составить структурный план здания. Теории пропорций и симметрии формируют фиксированные аспекты для всех видов архитектурных проектов. «Принципы гармонии» Пифагора наряду с геометрией использовались в архитектурных проектах шестого века до нашей эры. Мало того, что основы математики в сочетании с геометрией помогли повысить эстетику, гармонию и религиозную ценность больших сооружений, но также помогли уменьшить различные опасности, возникающие в результате высокоскоростных ветров.

Кроме того, лестницы во всех зданиях учитывают геометрические углы и построены под углом 90 градусов.

5. Искусство

Что включает в себя искусство? Искусство включает в себя формирование фигур и форм, базовое понимание 2-D и 3-D, знание пространственных концепций и вклад в оценку, модели и измерения. Из вышесказанного видно, что существует тесная связь между искусством и геометрией. Формирование форм является результатом использования геометрических форм, таких как круг, треугольник, квадрат, мандала или восьмиугольник. Более того, на содержание картин или скульптур во многом влияет выбор и форма рамы. Не стоит забывать, что принципы проективной геометрии составляют основу перспективы, которая используется в большей части живописи.

6. Спорт

Спорт часто не упускает единственной возможности использовать геометрические понятия. Здания спортивных стадионов и спортивных площадок учитывают геометрические формы. На спортивных площадках также используется геометрия; хоккейные, футбольные, баскетбольные и футбольные поля имеют прямоугольную форму. Точки углового удара, стойки ворот, дуги, D-секция и центральный круг отмечены на поле. Точно так же поля для различных других видов спорта, таких как волейбол и баскетбол, учитывают геометрические аспекты, потому что эти поля имеют четко обозначенные овалы, а также дуги окружности. Говоря о беговом поле, часто можно заметить полукруглые формы. Углы также играют решающую роль в прогнозировании движения игроков, повышении их производительности и подсчете очков.

7. Проектирование

Геометрия широко применяется в области проектирования; для создания анимированных фигур в видеоиграх требуется геометрия. В случае с искусством почти каждый элемент дизайна переплетается с геометрическими пропорциями, которые используются для изображения истории. На примере миниатюрных картин и иллюминации рукописей для составления макета используются геометрические принципы.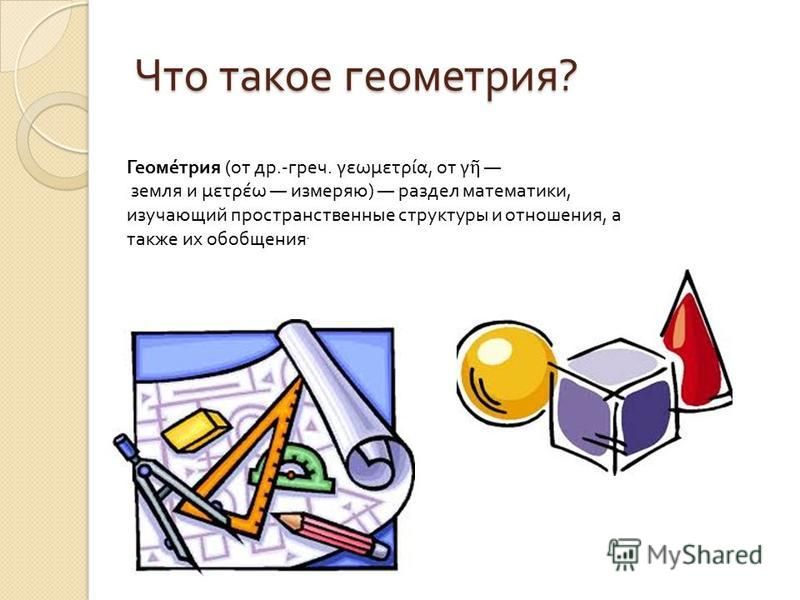 При формировании отдельных букв в каллиграфии уделяется внимание строгим геометрическим пропорциям. В дизайне геометрия играет символическую роль; как видно из резьбы на стенах, крышах и дверях различных архитектурных чудес.

8. Компьютерное проектирование – САПР

Геометрия, одно из основных понятий математики, включает в себя линии, кривые, формы и углы. Перед созданием любого архитектурного проекта компьютерное программное обеспечение помогает визуализировать визуальные изображения на экране. CAD, программное обеспечение, выдвигает план дизайна. Кроме того, это также помогает в моделировании архитектурных форм, что позволяет лучше понять готовый продукт. Принципы геометрии широко используются в различных промышленных процессах, что позволяет создавать графику.

9. Картирование

Геометрия помогает в точном расчете физических расстояний. Он используется в области астрономии для отображения расстояний между звездами и планетами и между разными планетами. Это также помогает в определении взаимосвязи между движениями различных тел в небесной среде. Помимо картирования расстояний между небесными телами, геометрия также играет жизненно важную роль в геодезии и навигации. В случае геодезии измерение площади земли является результатом точного определения формы земли. Кроме того, в навигации корабли, плавсредства и самолеты используют углы, а также зависят от других математических понятий для выполнения основных операций.

10. Медицина

Такие методы, как рентген, ультразвук, МРТ и ядерная визуализация требуют реконструкции формы органов, костей и опухолей, которая основана только на геометрии. Физиотерапия также использует геометрию. Геометрические свойства и функции помогают определить изображение в цифровых сетках. Геометрические концепции не только помогают в визуализации, манипулировании, сегментации изображений, коррекции и представлении объектов, но также играют важную роль в повышении стабильности, точности и эффективности. Методы биссектрисы и параллельные методы имеют решающее значение в радиологии.

11. Географические информационные системы

GPS спутников использует геометрические принципы для расчета положения спутников. Использование геометрии координат в Глобальной системе позиционирования (GPS) предоставляет точную информацию о местоположении и времени. GPS использует координаты для расчета расстояния между любыми двумя местами. Геометрия координат помогает GPS отслеживать транспортные происшествия и проводить спасательные операции. Координатная геометрия также помогает повысить безопасность полетов, прогнозирование погоды, мониторинг землетрясений и защиту окружающей среды. Более того, различные аспекты военных действий оснащены GPS.

Источники изображений

https://fineartamerica.com/
https://images-na.ssl-images-amazon.com/
http://lh4.googleusercontent.com/
http://s3.amazonaws. com/
https://www.britannica.com/
https://store.schoolspecialty.com/
https://ak7.picdn.net/
https://journal.eahn.org/
https://inspectapedia.com/
https://upload.wikimedia.org/
https://i.all3dp.com/
https://www.eg.bucknell.edu/

Геометрия в повседневной жизни, значение геометрии, приложения, геометрические фигуры, решенные примеры, практические вопросы, часто задаваемые вопросы

Геометрия является одним из наиболее важных разделов математики, так как она применяется в нашей повседневной жизни. Говорят, что геометрия происходит от греческого слова «гео-метрон», что означает гео и измерение соответственно. Это изучение 2D и 3D форм, которое применимо не только в классе, но и в искусстве, науке и повседневной жизни.

Геометрия влияет на нас в основных деталях нашей повседневной жизни, таких как выполнение сканирования, создание изображения или видео, строительство нашего дома, украшение дома и т. д. Список бесконечен, поскольку геометрия помогает поднять настроение. жизнь.

1.	Значение геометрии
2.	Применение геометрии в повседневной жизни
3.	Геометрические фигуры в повседневной жизни
4.	Решенные примеры
5.	Практические вопросы
6.	Часто задаваемые вопросы о геометрии в повседневной жизни

Значение геометрии

Одной из древнейших наук, существующих до сих пор, является геометрия. Это изучение математики, связанное с размерами, формами и фигурами, а также со свойствами пространства. Первоначально дети узнают все об основных формах, их свойствах, различных формулах, площадях и объемах, а также о способах рисования различных фигур в рамках урока геометрии. Но за эти годы он развился гораздо больше, что стало значительной частью нашей повседневной жизни.

В самом юном возрасте дети учатся пользоваться различными геометрическими инструментами, такими как транспортир, линейка и циркуль, которые помогают им строить основу для будущего, например, строить здания, делать чертежи, картографировать и т. д. Геометрия позволяет вам определить, как формы и фигуры сочетаются друг с другом, чтобы максимизировать эффективность и визуальную привлекательность. В повседневной жизни мы сталкиваемся с множеством практических ситуаций, когда нам нужно рассчитать определенное расстояние между объектами, вычислить размер фигуры, которую необходимо прикрепить в положении, для измерения и многое другое.

Применение геометрии в повседневной жизни

Геометрия используется в различных приложениях повседневной жизни, таких как искусство, архитектура, машиностроение, робототехника, астрономия, скульптура, космос, природа, спорт, машины, автомобили и многое другое. Некоторые из таких приложений, используемых в повседневной жизни, перечислены ниже:

Природа:
Одним из лучших примеров геометрии в повседневной жизни является природа.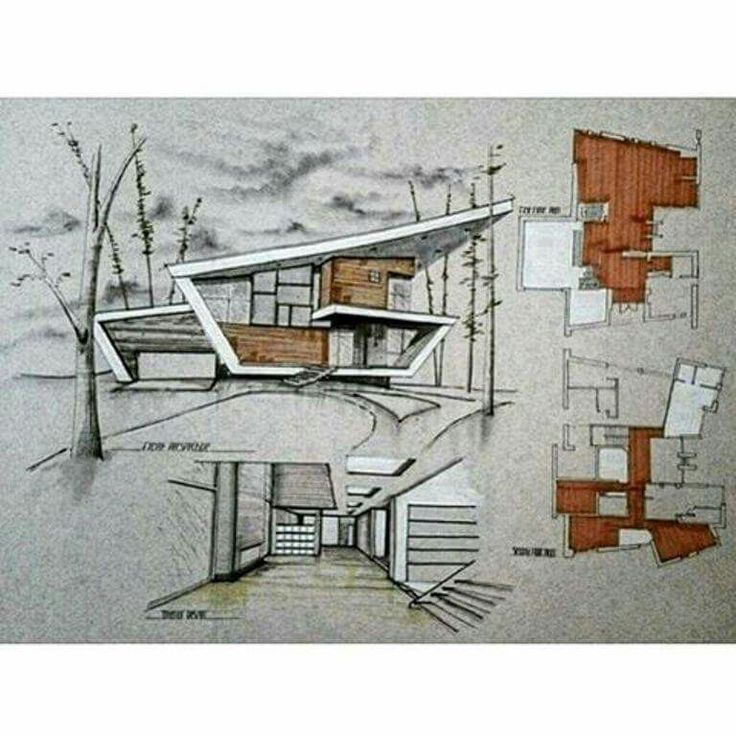 Мы можем найти различные геометрические формы и узоры в листьях, цветах, стеблях, коре и так далее. Ежедневная прогулка по саду поможет вам открыть для себя различные двухмерные и трехмерные геометрические формы и симметрию. Фрукты и овощи, которые мы ежедневно потребляем, имеют различную форму, что служит отличным примером для детей, чтобы пересмотреть свою геометрию. Одно из лучших в природе можно увидеть в улье, где пчелы строят свой дом в форме шестиугольника, который можно увидеть только в микроскоп.

Артикул:
Искусство по-разному связано с математикой, поскольку искусство требует знания различных форм и фигур, 2D и 3D форм, узоров и измерений. На содержание картины влияют и формы рам. Концепция перспективы для картины — это трехмерная фигура, которая отображается в двухмерном изображении. Следовательно, геометрия играет очень важную роль в искусстве.

Технические характеристики:
От представления форм на компьютере до создания различных дизайнов и планирования того, как схватить форму с помощью руки робота, до видеоигр — все они так или иначе используют геометрию. И компьютерам, и видеоиграм ежедневно требуется геометрия, поскольку проектирование и расчеты необходимы для их правильного функционирования.

Архитектура:
Конструкции зданий и памятников основаны на геометрии. Если вы когда-нибудь внимательно посмотрите на любое здание и памятник, вы обнаружите разные углы, линии и формы. Считается, что в древности геометрия была придумана для строительства зданий. В нашей повседневной жизни мы сталкиваемся с различными зданиями с различными формами и фигурами, это было сделано только с помощью приложений геометрии.

Спорт:
Всегда считалось, что дети, которые хорошо проявляют себя на поле, также очень хорошо учатся в классе. Дети, которые занимаются такими видами спорта, как футбол, крикет и бадминтон, преуспевают не только в спорте, но и в математике, особенно в геометрии. Каждый из этих видов спорта требует чувства направления и угла, чтобы направить мяч и забить идеальный гол. Геометрия играет важную роль в повседневной жизни, от бдительности на поле до распознавания их углов.

Геометрические фигуры в повседневной жизни

Когда вы осматриваетесь в своей спальне, классе или доме, какие различные вещи вы видите – разные предметы с разными формами и фигурами. От простых предметов первой необходимости, таких как телевизор, пульт от телевизора, мобильный телефон, ноутбук, простыни, диваны и т. д., до таких предметов, как игральные кости, используемые в настольных играх, ковры, вазы, картины и т. д., все имеет геометрическую форму.

Все эти объекты имеют граничные линии, углы и линии, имеющие двухмерную или трехмерную геометрическую форму. 2D-формы либо плоские, либо закрытые, такие как круги, квадраты, прямоугольники и т. д., а трехмерные формы, такие как куб, прямоугольный параллелепипед, конус, сфера и т. д., встречаются в нашей повседневной жизни. Большинство форм либо правильные, либо неправильные, правильные формы — это те, в которых есть симметрия, а неправильные формы — органические.

Важные моменты:

Геометрия является одним из основных аспектов математики, необходимых для нашей повседневной жизни.
Каждый день мы используем геометрию и геометрические фигуры, чтобы создавать что-то новое или использовать наши основные элементы, такие как книги, карандаши и многое другое.
Учащиеся практикуют навыки геометрии в повседневной жизни, которые они изучают в классе.

Часто задаваемые вопросы о геометрии в повседневной жизни

Кто изобрел геометрию?

Согласно древним временам, разные археологи находили изучаемую геометрию в Месопотамии и Египте во 2-м тысячелетии до нашей эры.

Кто отец геометрии?

Евклид известен как отец геометрии.

Почему геометрия важна в повседневной жизни?

Геометрия – это основная сущность, необходимая в нашей повседневной жизни. Будь то создание чего-то нового или использование существующего элемента, геометрия играет в этом важную роль. Мы видим геометрию в нашем окружении каждый день, и без геометрии мы не можем измерять, строить, создавать и поддерживать.

Какие геометрические фигуры используются в математике?

В основном в повседневной жизни мы видим два типа геометрических фигур — 2D и 3D. 2D-формы — это круг, треугольник, квадрат, прямоугольник, воздушный змей, трапеция, параллелограмм, ромб, а также различные типы многоугольников и 3D-фигуры — куб, параллелепипед, сфера, конус и цилиндр.

Где мы видим применение геометрии в нашей повседневной жизни?

Мы постоянно видим применение геометрии среди нас. Геометрию можно найти в искусстве, технике, природе, физике, медицине, спорте и многом другом. Чтобы все эти области функционировали, необходимо применение геометрии.

Полезна ли геометрия для студентов в повседневной жизни?

Геометрия — это математический предмет, который мы изучаем не только в классе, но и вне школы.

About Me

John Cena