Как сделать фигурки из длинного шарика: Как сделать собачку из воздушного шарика: пошаговая инструкция с фото
Как сделать собачку из воздушного шарика: пошаговая инструкция с фото
Одно из популярных занятий, как для детей, так и для взрослых – создание различных фигурок из воздушных шаров. Оно уже даже получило свое название – твистинг. Количество поклонников твистинга постоянно увеличивается. Это и не удивительно, ведь из воздушных шариков можно создать оригинальные фигурки и целые композиции. С помощью таких самоделок легко украсить помещение к празднику, сделать приятный сюрприз близким. А еще это очень весело и увлекательно! Тем, кто никогда не пробовал заниматься твистингом, следует начать из базовой модели – собачки. Как сделать собачку из воздушного шарика?
Шаг 1
Надуйте длинный шарик. Следите, чтобы он был надут не конца. Иначе существует риск, что во время работы шарик просто лопнет.
Шаг 2
Сделайте первую небольшую «сосиску». Это будет голова собачки.
Шаг 3
Делаем еще одну «сосиску».
Шаг 4
Вторую «сосиску» скручиваем вместе с остальным телом шарика.
Шаг 5
Скручиваем более длинную «сосиску» и делаем шею собаки.
Шаг 6
Начинаем делать лапы, как показано на фото.
Шаг 7
Сгибаем полученные «сосиски», и получаем две передние лапы.
Шаг 8
Скручиваем шарик, чтобы получилось туловище.
Шаг 9
Делаем задние лапы по тому же принципу, что и передние.
Шаг 10
Любуемся оригинальной собачкой из воздушного шарика!
Сделайте свой праздник необыкновенным! Закажите у нас – https://sharonline.ru яркие воздушные шары, которые станут отличным украшением дня рождения, свадьбы, Нового года и других веселых мероприятий!
Цветок из длинных шариков
Цветок из шариков для моделированияЦветок из длинных воздушных шариковДля одного цветка из шариков нужно:
- 1 длинный шарик для моделирования желтого или салатового цвета
- 1 длинный шарик для моделирования любого другого цвета по желанию
- насос для накачивания шариков
Как сделать цветок из длинных шариков:
1. Сначала надуваем синий шарик полностью. Потом сдуваем его так, чтобы диаметр колбаски уменьшился и в начале образовался хвостик 7-8 см. Чем мягче получится колбаска, тем удобнее будет проворачивать лепестки — это будет самое сложное во всей работе. Ребенок вряд ли справится самостоятельно — нужно будет ему помочь.
Сначала надуваем синий шарик полностью. Потом сдуваем его так, чтобы диаметр колбаски уменьшился и в начале образовался хвостик 7-8 см. Чем мягче получится колбаска, тем удобнее будет проворачивать лепестки — это будет самое сложное во всей работе. Ребенок вряд ли справится самостоятельно — нужно будет ему помочь.
2. Концы шарика связываем между собой.
3. Делим колбаску посередине и делаем скрутку в 2 оборота.
4. Двойную колбаску условно делим на 3 равные части и скручиваем. Чем равномернее поделите, тем одинаковее получатся лепестки и аккуратнее цветок. Я немножко схалтурила
5. Складываем разделенную колбаску зигзагом.
6. Перехватываем пальцами, объединяя все скрутки. Теперь нужно провернуть три правых колбаски относительно трех левых — колбаски согнутся, формируя лепестки, а скрутки образуют жесткий замок.
Как сделать цветок из длинных шариков ч.27. Вот так выглядит скрученный цветочек. Осталось прикрепить его на стебелек.
8. Для этого надуваем шарик желтого цвета, оставив ненадутым хвостик 7 см, завязываем. Хвостик указательным пальцем правой руки проталкиваем внутрь шарика.
9. Перехватываем хвостик пальцами левой руки и делаем скрутку, фиксируя положение хвостика.
10. Вставляем стебелек в месте скрутки между лепестками цветка. У цветка сформировался красивый центр.
Как сделать цветок из длинных шариков ч.311. Осталось сделать листики на цветочной ножке. Отступаем от цветка произвольное расстояние и делаем скрутку. Потом отделяем скрутками 2 колбаски равной длины.
12. Складываем колбаски друг с другом и скручиваем вместе у основания — получился первый лепесток.
13. Этот лепесток сворачивает стебелек под углом, чтобы стебелек был ровный, нужно сделать парный листик.
14. Под первым листиком делаем еще две таких же колбаски. Складываем их вместе и скручиваем, как в пункте 12.
Вот и готов цветочек на стебельке с двумя листиками из шариков для моделирования!
Вот такой получился цветочек из длинных шариковДелаем произвольное количество цветочков, объединяем в букет и дарим любимым или дорогим сердцу людям
Еще интересненькое на сайте:
Из воздушных шаровРоза из воздушных шаровСобака из шарика колбаскиТюльпан из воздушных шаровРоза из шариков в бокалеУтка из длинного воздушного шарикаКак научиться делать фигурки из шариков
Несомненно многие люди любят воздушные шарики, они вызывают восторг и хорошее настроение, но как-то по-особенному смотрятся воздушные фигуры из них. Торжество выглядит более нарядным и красочным, а впечатления от него – незабываемыми.
Торжество выглядит более нарядным и красочным, а впечатления от него – незабываемыми.
С течением времени появилось такое направление, как твистинг – от английского слова «скручивать», которое представляет из себя моделирование воздушных фигур из специальных шаров, созданных именно для этих целей.
Научится скручивать шарики и создавать воздушные фигуры реально, нужно лишь запастись терпением, прочными шариками и специальным насосом. Фигуры из шариков могут стать украшением праздника, подарком или простым декором в комнате. Особенно интересно будет обучаться искусству твистинга с детьми: сам процесс обучит усидчивости, терпению и аккуратности, а результат непременно обрадует ребенка.
Что понадобится для твистинга
Начать следует с подбора основных материалов, которые понадобятся в обучении скручивания и создания фигур из длинных шаров. Для начала потребуется только несколько предметов, а после приобретения определенных навыков набор может увеличиваться:
- Длинные воздушные шары или ШДМ (шары для моделирования).
 К выбору шариков нужно подойти серьезно, поскольку от этого зависит качество и прочность фигуры.
К выбору шариков нужно подойти серьезно, поскольку от этого зависит качество и прочность фигуры. - Поршневой двухходовой насос – важный инструмент в работе с длинными шариками, потому что прочные шары надуть без ручного насоса практически невозможно. Иногда насос продается в наборе с ШДМ.
- Ножницы, маркер и другие вспомогательные предметы.
Перед тем, как надувать длинный шарик, его рекомендуется немного размять – растянуть несколько раз руками для разогрева латексного материала, тогда работать с шариком будет гораздо легче.
Правила крепких фигурок из длинных шариков
После разогрева, шарик нужно растянуть в длину и надеть отверстием на кончик насоса. Надувать шары стоит неторопливо и равномерно. Обязательно нужно оставить небольшой хвостик, чтобы туда уходил воздух и при скручивании шарик не лопнул, как правило это около 10 см. Толщина шарика зависит от вида фигуры, можно ориентироваться поэтапным инструкциям.
Как только шарик достигнет нужной длины и ширины, его нужно аккуратно снять с насоса и затянуть кончик узелком. Нитки для ШДМ не подходят.
Нитки для ШДМ не подходят.
Важное правило крепкой фигуры: скручивать ее только в одну сторону, например по часовой стрелке. Обязательно нужно придерживать пальцами скрученные места, так как в любой момент фигура может раскрутиться и время потраченное на нее, пройдет даром.
Виды скручивания
Чтобы получить воздушную фигурку в виде какого-либо животного или цветка, длинный надутый шарик скручивается в пузыри разной длины, а потом соединяется в замок. В зависимости от типа фигуры, различают следующие виды скручивания:
- Обычное скручивание – закручивание маленького пузыря на шарике. Определяется размер пузыря и сжимается рукой на этом расстоянии, затем скручивается в одну сторону примерно 3-4 раза. Последующие пузыри скручиваются в ту же сторону.
- Скручивание с замком – закрепление 3-х подряд идущих пузырей в конкретную фигуру. Складываются 2 крайних пузыря в месте их соединения, затем скручиваются вокруг со следующим в этом же месте 3-4 раза.

- Скручивание с замком (еще один способ). Скручивается два пузыря и шарик сгибается в месте последнего скручивания, сжимается рабочая часть и намечается следующий пузырь и только потом скручивается вместе.
- Скручивание со сгибом – закрепление трех последовательно идущих пузыря в фигурку, где два крайних не скручены, а просто согнуты. Скручивается пузырь, шарик перегибается и перекручивается 2-3 раза.
Виды скручивания можно отработать на шариках до преступления к твистингу, чтобы обрести навык ловкости рук. Когда техника скручивания отработана на практике, понимать инструкцию по формированию фигур и следовать ей, будет гораздо проще.
Фигуры из длинных воздушных шариков
Некоторые воздушные фигурки сделать не сложно, нужно лишь придерживаться пошаговой инструкции. Также у каждой фигуры есть свои особенности, поэтому требуется внимательность и усидчивость – возможно получится не сразу, но не стоит отчаиваться, твистинг любит настойчивость.
Собачки
Самая распространенная фигура из длинных шариков – это пудель. Сделать собачку не трудно, придерживаясь следующей инструкции:
- Накачать шарик с помощью насоса и оставить не надутую часть примерно 8 см.
- Сделать три пузыря размером примерно 4 см, первая – это мордочка пуделя, зафиксировать ее пальцами (чтобы не раскрутилась).
- Отступить один пузырь и скрутить замком.
- Сделать еще три одинаковых по размеру скрутки и скрутить замком так, чтобы получилась петля – это ножки пуделя.
- Скрутить еще 4 пузыря.
- Отступить один пузырь, сделать еще раз замок.
- Получилась собачка, но перевернутая, остается развернуть мордочку и поднять вверх хвостик – фигура готова.
Если опустить ушки вниз, а тело немного удлинить – получится такса.
Цветы
Сделать цветок из длинных шариков немного труднее. Здесь потребуется уже три шарика:
- Оттенок лепестков: красный, розовый, оранжевый, белый и др.
 ;
; - Цвет стебля и листика, как правило выбирают зеленый, но можно экспериментировать;
- Цвет серединки цветка: желтый или оранжевый.
Начинать создание цветка лучше с лепестков.
- Надуть яркий шарик насосом, оставить хвостик размером в 3-4 см, завязать отверстие узелком.
- Замкнуть начало шарика и его конец – связать их, чтобы получилась окружность.
- Сложить окружность пополам и скрутить три пары пузырей, так, чтобы это напоминало двойной ряд связанных сосисок.
- Теперь нужно сложить эту связку гармошкой, как показано на схеме 5-6.
- Сдавить пальцами посередине и скрутить в общую скрутку, получится 6 лепестков.
- Можно приступить к стеблю, надуть весь зеленый шарик насосом, но не делать его слишком плотным, потому что на стебле будут еще два листика.
- От завязанного узелка следует отступить около 10 см и скрутить, а потом получившуюся скрутку согнуть напополам и перекрутить еще раз, так, чтобы получилась двойная скрутка.

- Можно вставить получившиеся скрутки стебля в лепестки, а можно надуть желтый шарик (или другого цвета) и сделать из него сердцевину, предварительно обрезав лишнюю часть после скрутки.
Для сердцевины подойдет и круглый шарик, если надуть его тоже не полностью, и закрепить обычным узлом к стеблю.
- Для создания листиков на стебле, достаточно выполнить скручивание с перегибом и выровнять полученные листики – цветок готов.
Более эффектно смотрятся букеты из воздушных цветов, они достаточно крупные, поэтому для праздника вполне хватит 5-7 таких цветков, перевязанные красивой широкой лентой.
Если оставить лепестки на этапе гармошки, как на схеме 6 рисунка 4, а затем сцепить со стеблем – получатся очаровательные тюльпаны, которые можно подарить на 8 марта.
Сейчас есть много вариаций как сделать цветы из длинных шариков, существуют разные схемы и методы, которые доступны не каждому новичку, но можно достаточно легко сделать очаровательные лотосы, или водяные кувшинки, которые эффектно будут смотреться в воде или на столе.
Итак, для того, чтобы создать прекрасный лотос, потребуется:
- Два шарика розового/белого/красного или других цветов – для лепестков;
- Один шарик желтого цвета для сердцевины;
- Один шарик темно-зеленого оттенка;
- Насос и ножницы.
Перед тем, как надувать шарики, их нужно немного размять и потянуть, потомучто для лотоса предстоит много скруток.
Зверушки
Если получилась собачка, получатся и другие зверушки. Техника скручивания фигуры в жирафа очень похожа на моделирование собачки, есть некоторые отличия:
- Делая жирафа, голову нужно смоделировать поменьше, а на мордочку оставить всего 2-3 см;
- После мордочки будет не 5 скруток, а 4;
- Шея жирафа будет длиннее и это нужно учесть при скручивании;
- Тело получится короче, а хвостик меньше.
Нетрудно смоделировать и зайчика, методика очень схожа с собачкой. Для зайчика потребуется один шарик, насос и маркер, для завершения образа.
- Надуть шарик насосом и оставить примерно 8 см не надутого хвостика.
- Скрутить первый пузырь, длинной в 8 см – это голова зайца.
- Скрутить еще два пузыря – это ушки зайчика.
- Скрутить следующий пузырь, размером около 13 см, повторить это действие еще раз.
- Соединить два конца цепочки двух крайних скруток в замок.
- Скрутить следующий пузырь длиной всего 2-3 см – это будет шея животного.
- Дальнейшее скручивание будет выполнятся для передних лапок зайца: скрутить пузырь около 5 см, следующий 2-3 см, следующий такой же 2-3 см, и еще один – 5 см.
- Соединить цепочку из последних 4-х скруток в единый замок – передние лапки сделаны.
- Скрутить пузырь размером в 5 см – это туловище животного.
- Осталось скрутить пузыри для задних лапок: сделать скрутку длиной в 15 см и соеденить оба конца в замок.
- Еще один пузырь – маленький хвостик.
Чтобы завершить моделирование зайчика остается только развернуть все части тела на свои места, собрав в фигуру зайца. Для полного завершения можно подрисовать глазки, носик и усики – зайка готов.
Для полного завершения можно подрисовать глазки, носик и усики – зайка готов.
Также не особо сложно сделать тигра или кошку. Схема моделирования у этих животных одна, а расцветка меняется.
- Надуть шарик насосом, оставить хвостик, незаполненный воздухом 13-14 см, снять с насоса и завязать отверстие в узелок. Всего будет 11 скрученных пузырей.
- Скрутить 7 небольших пузырей, придерживая руками.
- Между 2 и 3-ей скруткой сделать еще одну, между 4 и 6 такую же.
Моделирование лба, челюсти, ушей и щек тигра/кошки:
- Взять первый пузырь и просунуть внутрь тигринную мордочку, придерживая ее с внешней стороны, обернуть этот пузырь между 8 и 9-ым пузырем – проявится нос и рот тигра, а 4-ый и 6-ой пузыри – это уши.
- Туловище и лапы животного моделируется вместе. Связать концы шарика двойным узлом и поделить напополам, останется два пузыря – это задние лапки.
Получившаяся фигура из длинных шариков будет выглядеть более похожей на тигра, если маркером дополнить образ: нарисовать глаза, нос, усы и характерные полоски.
По этой же методике моделируется кошка, только расцветка будет отличаться.
Птички
Из длинных шариков можно сделать что угодно и кого угодно, в том числе и птиц. Особо распространены лебеди. Чтобы смоделировать из лебедя, нужен только один шарик, белого или светло-желтого цвета.
- Надуть шар с помощью насоса и оставить небольшой хвостик около 6 см, он нужен для скручивания и для будущего клюва птицы.
- Сформировать кольцо из большей части шара и придерживать пальцами, другой рукой согнуть кольцо напополам.
- Скрутить каждое колечко по отдельности и вдеть одно кольцо в другое, сформировать в туловище птицы.
- Оставшаяся часть – это шея и голова, ее необходимо осторожно согнуть и подержать некоторое время, чтобы шар принял форму.
- Дорисовать лебедю глазки и оформить клювик – птица готова.
Не стоит боятся скручивать, даже если в схеме очень много подобных действий, шарик не лопнет: во-первых, остается место для воздуха, во-вторых шарики изготовлены из латекса и имеют высокую эластичность, а в третьих – перед надуванием шарик подлежит разогреву и растяжке.
Заключение
Как видно, если есть схема и описание, сделать фигурки из воздушных длинных шариков не трудно. Постепенно, от легких фигур, можно переходить к более сложным схемам моделирования, приобретая все больше навыков скручивания и ловкости рук.
В Японии живет невероятный мастер твистинга, создающий из шаров целые шедевры, а ведь он тоже когда-то начинал с собачек и цветочков.
Воздушные шарики занимают почетное место в праздничном декоре и десятилетиями остаются детскими любимцами. Они обладают удивительным свойством – мгновенно поднимать настроение и дарить улыбку. Конечно, даже просто связка смотрится ярко и нарядно, но фигуры из воздушных шариков приводят в восторг и детей, и взрослых. Думаете, этому искусству сложно научиться? Как раз нет, главное – внимательно следовать инструкциям.
Правила работы
- Если вы решили заниматься творчеством на основе воздушных шариков, то лучше всего обзавестись ручным насосом.
 Причем не забывайте надувать их не до конца, оставляя пустой хвостик. Это необходимо для того, чтобы шарик не лопнул во время скручиваний. Чем сложнее ваши фигуры, тем больший хвостик нужно оставлять.
Причем не забывайте надувать их не до конца, оставляя пустой хвостик. Это необходимо для того, чтобы шарик не лопнул во время скручиваний. Чем сложнее ваши фигуры, тем больший хвостик нужно оставлять. - Работа всегда начинается от завязанного конца шарика. Так воздух может передвигаться в свободное пространство.
- Если воздушные шарики часто лопаются, обратите внимание на свой маникюр и одежду: заусенцы на пальцах, часы, цепочки могут незаметно для вас рвать их.
- Скручивания можно выполнять в любую сторону, но в рамках конкретного изделия всегда придерживайтесь одного направления.
Основные элементы моделирования
Прежде чем начать изучать, как делаются фигуры из шариков, давайте рассмотрим две техники для работы с шариками:
- Скрутка — основной прием. Надутый шарик следует взять со стороны узелка левой рукой, если вы правша. Захватите столько места, сколько указано в инструкции (например, 5 или 10 см). Затем правой рукой проверните длинный конец шарика, чтобы создать отделенную секцию.
 Обратите внимание, что если вы отпустите ее, она распрямится. Чтобы избежать этого, вам понадобится следующий прием.
Обратите внимание, что если вы отпустите ее, она распрямится. Чтобы избежать этого, вам понадобится следующий прием. - Закрепляющая скрутка, или «замок». Чтобы выполнить ее, вам понадобится сделать еще 2 сегмента колбаски. Держите их левой рукой, чтобы они не раскрутились. Затем возьмите левой рукой 2 внутренних сегмента, уложите их параллельно друг другу и прокрутите трижды у основания. Теперь они будут держаться на месте.
Классика жанра
Это, конечно же, фигуры из шариков «колбасок» в виде собачек разных форм и размеров. Давайте рассмотрим, как они делаются.
- Для этой поделки вам понадобится один длинный шарик.
- Надуйте его, оставив не менее 5 см колбаски пустыми. Теперь трижды скрутите шарик: первый кусочек должен быть длиной около 5 см – это будет морда собаки, второй и третий – по 2,5 см, для ушей.
- Выполните закрепляющую скрутку, т. е. возьмите «уши» в одну руку параллельно друг другу и оберните трижды вокруг «мордочки».
- Получившаяся фигурка должна напоминать голову собаки.

- Теперь сделайте еще 3 скрутки длиной 7-8 см. Первая будет шеей собаки, вторая и третья – ее передними лапами.
- После этого поступите со 2-м и 3-м сегментом так же, как и с ушами: придерживая левой рукой, разместите их параллельно друг другу и сделайте «замок».
- Вы уже, наверное, догадались, как завершить работу. Сделайте 3 скрутки длиной 7-8 см. Первая – это туловище, вторая и третья – это задние лапы пса, ну а оставшийся кусочек шарика – это хвост. Придерживая все части «колбаски», сделайте закрепляющую скрутку для лап. На этом пес готов. Можно нарисовать маркером глазки и носик, а можно приклеить готовые наклейки-глаза.
Мини-зоопарк
Когда вы научитесь делать обычную собачку, перед вами откроется небывалый простор для творчества. Меняя пропорции, можно менять внешний вид фигурки, например, очень короткие лапки и длинное туловище помогут создать таксу. Больше скруток в районе ушей и на лапах (для этого вам понадобится очень длинный белый шарик) – и у вас получился пудель.
А как сделать жирафа? Проще простого: возьмите желтый шарик, у обычной собачки сделайте непропорционально длинную шею, удлините ноги и нарисуйте пятна черным маркером.
Для настоящих рыцарей
Мечи из воздушных шариков пользуются огромным успехом на детских (и не только) праздниках. Только не забудьте изготовить побольше такого оружия, ведь в пылу боя оно часто лопается и требует замены.
Как же делаются такие фигуры из шариков? Инструкция довольно проста, но познакомит вас еще с одним новым приемом работы.
- Итак, вам понадобится один шарик, надуйте его, оставив 2,5 см пустыми.
- Сделайте скрутку длиной примерно 12-13 см. Это рукоятка меча.
- Теперь вам нужно сделать складывающуюся скрутку. Для этого согните шарик так, чтобы у вас получился сгиб длиной 7-8 см, и плотно закрутите его на уровне первой скрутки. Это половина гарды.
- Повторите операцию с другой стороны, тщательно следя, чтобы размеры сегментов шарика были одинаковыми.

- Расправьте гарду. Если нужно, то слегка промните воздух в шарике, чтобы он заполнил пустой кончик. На этом меч готов.
Для морских волков
Еще одни интересные фигуры из шариков — это пиратские сабли. Они делаются быстро и легко:
- Надуйте шарик, оставив 2-3 см пустыми. Сделайте очень маленький сегмент – длиной 2-3 см, не отпуская его, выполните складывающуюся скрутку, которая займет около 15 см.
- В получившееся кольцо проденьте длинный конец шарика так, чтобы у вас получилась удобная рукоятка. Распределите воздух по шарику, придайте ему изгиб, и сабля готова.
Чтобы рукоятка была красивее, можно сделать 5 очень маленьких скруток, перед тем как продевать длинную часть шарика в петельку.
Воздушная флористика
Предыдущие фигуры из шариков в основном используются как игрушки для детей, а вот цветы, сделанные в такой технике, находят применение и в декорировании помещений.
Вот один из способов, как их можно делать:
- Возьмите яркий шарик и надуйте его, оставляя около 5 см пустыми.
 Сразу выполните складывающуюся скрутку длиной около 10 см. Это первый лепесток.
Сразу выполните складывающуюся скрутку длиной около 10 см. Это первый лепесток. - Точно так же сделайте еще 4 скрутки. Старайтесь, чтобы они были одинакового размера.
- Расправьте лепестки.
1. Теперь возьмем зеленый шарик и приступим к изготовлению стебля. При надувании нужно оставить 2-3 см пустыми.
2. На расстоянии 30 см от завязки шарика сделайте 2 складывающихся скрутки – по большому счету, у вас получится меч, описанный выше. Но теперь это будут листики цветка.
3. Сделайте маленькую скрутку – длиной около 2-3 см и протолкните ее в центр цветка.
На этом можно и закончить.
Хотите сделать более нарядный цветок? Добавьте скрутки на кончиках каждого лепестка. Но не забудьте оставить больше пустого места в шарике, чтобы он не лопнул в процессе.
Как видите, искусство создания фигурок из шариков технически простое, но требует от вас пространственного мышления и фантазии, чтобы уметь представить обычный предмет в виде последовательности скруток. Но, как и любое творчество, этот процесс очень увлекательный.
Но, как и любое творчество, этот процесс очень увлекательный.
Интересные фигуры, сворачиваемые мастерами из воздушных шариков не могут оставить равнодушными ни одного ребенка. Но зачем вызывать мастера, если можно сделать такие фигурки своими руками. Из них можно изготовить почти любых животных – пуделя, жирафа, лебедя и даже тигра, а также другие предметы, например цветок или меч. О том, как это сделать мы расскажем и покажем в этой статье.
Общие рекомендации по изготовлению фигурок из шариков- Чтобы надуть шарики рекомендуется использовать ручной поршневой насос.
- Не надувайте шарик слишком плотно, так как при дальнейшем скручивании он может лопнуть. Оставьте хвостик 4-5 сантиметров
- Кончик шара завяжите в узел. Не завязывайте кончик с помощью ниток.
- Скрутки необходимо делать только в одну сторону. Если делать в разные то фигура имеет все шансы развалиться.
Собачка, чаще всего пудель, является одной из самой распространенной фигурок из длинных шариков. Ее изготовление не является особо сложным и под силу даже новичкам. Схема изготовления пуделя выглядит следующим образом:
Ее изготовление не является особо сложным и под силу даже новичкам. Схема изготовления пуделя выглядит следующим образом:
Также можете ознакомиться с видео инструкцией по изготовлению собачки из воздушного шарика:
Как сделать меч из шарикаМеч из шариков придется по нраву мальчишкам. В изготовлении он еще проще чем собачка. Схема изготовления меча выглядит следующим образом:
Видео инструкция по изготовлению меча из шариков:
Как сделать цветок из шариковЭта фигура также довольна легка в изготовлении, но для нее потребуется несколько длинных шариков. Одним из плюсов данной фигуры является ее универсальность. Их можно использовать на детских праздниках, а также для украшения интерьера. Схема изготовления ландыша выглядит так:
Схема для изготовления лотоса представлена следующим образом:
Видео инструкция по изготовлению простого цветка из шариков:
Как сделать зайца из шариковЕще одним долгожданным гостем на детских праздниках является заяц.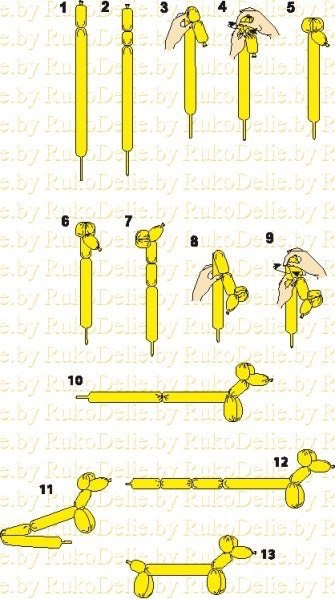 Изготавливается он из нескольких шариков, а потом маркером рисуется его мордочка. Видео инструкция по изготовлению зайца из шариков:
Изготавливается он из нескольких шариков, а потом маркером рисуется его мордочка. Видео инструкция по изготовлению зайца из шариков:
Лебедь – одна из самых прекрасных птиц. Это одна из самых простых композиций, которые только можно скрутить. Схема изготовления лебедя из шарика:
Видео инструкция по изготовлению лебедя из шарика:
Фигурки из воздушных шаров: схемы и инструкция прилагается
И взрослые, и дети любят большое количество воздушных шариков. Для украшения праздничных мероприятий используют яркие и красочные комбинации этого латексного изделия. Фигурки из самых обычных воздушных шаров могут доставить радость совершенно любому ребенку и даже взрослому человеку.
Мы предлагаем вам научиться самостоятельно изготавливать необычные и оригинальные композиции из воздушных шариков. Это увлекательное занятие позволит вам создавать композиции из латексных изделий и украшать при помощи их свои праздничные мероприятия и события.
Делаем фигурки из воздушных шаров: история развития твистинга в мире
Простые фигурки из шаров могут создавать дети и взрослые, это интересное увлечение, чтобы избавиться от стресса и весело провести время. В настоящее время в нашей стране это искусство не приобрело широкой популярности, однако в Америке оно активно развивается в течение всего двадцатого века. Впервые номер со скручиванием резиновых шариков появился во время циркового представления в 1938 году, однако массовая популярность пришла только после запуска производства длинных воздушных шариков, которое произошло после Второй Мировой войны.
Качество резиновых шаров улучшилось в начале 60-х годов, они стали более тонкими и прочными, да и палитра цветов расширилась, к тому же, они стали более дешевыми, что позволяло распространиться твистингу в широких массах. Шары стали длинными: их длина теперь стала больше диаметра практически в двадцать раз, что позволяло выполнять много скручиваний.
Как правильно создавать фигурки из воздушных шариков своими руками?
Для того чтобы начать процесс изготовления композиций из латексных шариков, необходимо знать минимальные основные знания и основы твистинга. Сначала рекомендуется начинающим и неопытным мастерам пробовать свои навыки на изготовлении элементарных элементов и схем композиций.
Сначала рекомендуется начинающим и неопытным мастерам пробовать свои навыки на изготовлении элементарных элементов и схем композиций.
Сначала вам следует освоить навыки правильного надувания длинных шаров-колбасок. Для накачивания воздушного материала удобнее всего использовать специальный насос. После того как вы наполните свой шарик воздухом до необходимой вам длины, вам следует немного спустить воздушной массы. Это позволит избежать излишнего давления на тонкие стенки латексного материала.
Скручивать шарики-колбаски следует всегда только по направлению от горловины конструкции. Воздух, который располагается внутри шарика, должен продвигаться к «хвосту» вашего изделия.
Основополагающим требованием в процессе твистинга является выполнение всех скручиваний в одном направлении и только при помощи одной руки. В скручивании должны быть использованы все пальцы вашей ладони, иначе ваша конструкция разрушиться и вам придется начинать все заново.
Создадим милую собачку из воздушных шариков: делаем своими руками
Предлагаем вам простую и подробную инструкцию по изготовлению собачки из воздушных шариков. Возьмите длинный шарик любого цвета и наполните его воздухом. Затем сожмите латексный шарик одной рукой, а второй рукой совершите простое скручивание конструкции вокруг своей оси несколько раз.
Возьмите длинный шарик любого цвета и наполните его воздухом. Затем сожмите латексный шарик одной рукой, а второй рукой совершите простое скручивание конструкции вокруг своей оси несколько раз.
После этого сформируйте три небольших пузырика на колбаске шара и загните на стыке. Затем потяните вверх и перекрутите вокруг данных стыков три раза. Зафиксируйте конструкцию так, чтобы она не раскрутилась.
Далее сделайте три пузыря диаметром около 2.5 сантиметров. Крайние пузыри удерживайте, средний потяните очень аккуратно и перекрутите его три раза вокруг своей оси.
Прием «с перегибом» также предполагает, что в самом начале вы сформируете три пузыря, однако средний должен быть больше всех остальных. Теперь необходимо удерживать крайние, потянуть за средний шарик и, сложив его пополам, перекрутить три раза.
Прием «тюльпан» — указательным пальцем необходимо протолкнуть узелок внутрь длинного шарика на длину двух фаланг, а второй рукой взяться за узел с внешней стороны, крепко придерживая его, а затем вытащить палец из шарика. Скручивать следует таким образом, чтобы узел находился ниже, и вы увидите, как образовался тюльпан.
Скручивать следует таким образом, чтобы узел находился ниже, и вы увидите, как образовался тюльпан.
Очередной прием называется «с хлопушкой» и выполняется по следующей схеме: первый пузырь необходимо скрутить среднего размера, далее будет идти серия из пяти маленьких пузырьков. Первый и последний пузырьки маленького размера необходимо скрутить, таким образом, чтобы сформировалось кольцо, затем скрутите второй и четвертый в «ухо». После таких манипуляций вы заблокировали средний пузырек.
Видео по теме статьи
Предлагаем посмотреть несколько интересных и подробных видео по теме статьи. Приятного просмотра.
youtube.com/embed/xjKloF3gshw?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Как сделать из шарика зайца
Попробуйте освоить технику твистинга, и вы не только в любой момент сможете порадовать своих малышей веселыми фигурками из шариков, но и станете звездой на любом празднике! В результате работы над мастер-классом у нас родился вот такой солнечный заяц из шариков — вы без труда его сможете повторить, а при необходимости — по аналогии создать фигуры и других зверушек.
Чтобы сделать зайца из шариков, понадобятся:
длинные воздушные шары-колбаски для моделирования;
насос.
Заяц из воздушных шаров своими руками: описание работы
Если в доме насоса нет и вы только планируете его купить, обратите внимание на его характеристики: лучше, если насос будет двухфазным, тогда воздух будет набираться быстрее и легче.
Надеваем шарик на насос и накачиваем, придерживая край отверстия большим и указательным пальцами.
Не надуваем шарик до конца: нужно оставить хвостик длиной 10 см: при скручивании фигурки в этот запас будет уходить воздух.
Немножко спускаем шарик, чтобы он стал не слишком тугим, и завязываем кончик на узел.
Вот так выглядит подготовленный для скрутки шарик.
Приступаем собственно к созданию зайца. Моделируем мордочку зайчика: скручиваем один маленький шарик и два продолговатых – будущие уши.
Важно: делайте все скрутки в одном направлении.
Первую и третью скрутку соединяем, перекручиваем между собой и… мордочка готова!
Далее следует маленький шарик – шея. Продолжаем скручивать в одном направлении.
Два продолговатых пузырика делаем для формирования передних лапок.
Соединяем их с шеей и перекручиваем.
Следующий шарик-колбаска — для животика зайки.
Оставшуюся часть шарика заворачиваем «баранкой», оставляем чуть-чуть воздуха для хвостика и скручиваем.
В получившееся колечко вставляем передние лапки.
Воздушный заяц из шариков готов!
Вы можете устроить целое представление, делая игрушку из воздушных шаров на глазах у малышей, а можете подключить и самих детишек — им этот процесс, несомненно, понравится.
Елена Моденова специально для сайта Мастер-классы по рукоделию
Как сделать собаку из шарика
ШДМ — шары для моделирования .
Хорошее настроение ассоциируется с праздником, а праздник – с красивым оформлением помещения, где он проходит. А если у ребенка день рождения, то без воздушных шаров не обойтись. Конечно, эти разноцветные шарики и сами по себе могут служить отличным декором, но если включить фантазию, то их легко превратить в любое животное или целую композицию.
Милая собачка из длинного воздушного шарика – это базовая поделка, которую следует научиться делать тем, кто хочет скручивать из шаров разнообразные фигурки. Для моделирования фигурок можно использовать много видов воздушных шаров продолговатой формы, но с шарами 260 и 260-2 работать удобнее всего. Они эластичные, крепкие, безопасные. Именно такими свойствами обладает натуральный латекс, который используется для производства воздушных шариков. Они не лопают при надувании ртом.
Они эластичные, крепкие, безопасные. Именно такими свойствами обладает натуральный латекс, который используется для производства воздушных шариков. Они не лопают при надувании ртом.
В нашем мастер-классе мы расскажем, как делать собаку из шарика. Готовы?
Нам понадобятся:
- воздушный шарик 260;
- насос (при наличии).
- Если под рукой нет насоса, то собачку из шариков своими руками можно сделать при помощи обычной резиновой груши. Однако перед тем, как надувать шар, слегка растяните его, потянув за оба конца. Если надуваете ртом, следите, чтобы щеки не раздувались слишком сильно, так как это может стать причиной разрыва мельчайших капилляров, а на лице появится синеватая «сеточка». До конца шар надувать не следует, необходимо оставить «хвостик» длинной около 8-10 сантиметров. Это необходимо для того, чтобы при скручивании воздух из каждой «колбаски» (составляющих элементов нашей собачки из шарика) мог перемещаться в эту часть. Хорошенько завяжите кончик.
 Теперь со стороны узелка отступите на 5 сантиметров и сделайте 5-6 оборотов, чтобы получилась «колбаска». Таким же образом сделайте еще две колбаски, но немного меньшего размера (3-4 сантиметра). Первая будет служить мордочкой собачки, а две других – ушками.
Теперь со стороны узелка отступите на 5 сантиметров и сделайте 5-6 оборотов, чтобы получилась «колбаска». Таким же образом сделайте еще две колбаски, но немного меньшего размера (3-4 сантиметра). Первая будет служить мордочкой собачки, а две других – ушками.
- Согните шарик как показано на фото, а затем оборотами зафиксируйте уши, которые обозначены буквами В и С. Должна получиться голова – мордочка с ушками.
- Три следующие «колбаски», скрученные таким же образом, будут служить шеей и передними лапками собачки. Как видите, шарик уже отдаленно напоминает собачку.
- И последние четыре «колбаски», где А – это, собственно, тело собаки. В и С – ее задние лапки, а D – это хвостик. Размер тельца и хвостика может быть каким угодно, а вот задние лапки не только должны быть одинаковыми о длине относительно друг друга, но и совпадать в размерах с передними.
 Вот и все, что необходимо для того, чтобы сделать собачку из шарика, как просто, не правда ли?
Вот и все, что необходимо для того, чтобы сделать собачку из шарика, как просто, не правда ли?
Как уже упоминалось выше, собачка – это базовая поделка из шариков. Если вы освоили принцип ее моделирования, то можете поэкспериментировать с длиной «колбасок». Так, при удлинении «колбаски», которая служит тельцем, у вас получится забавная такса. Сделайте на хвостике дополнительный шарик – вот и готов веселый пудель, а если удлинить шею и ноги, то выйдет жираф.
Когда моделирование из воздушных шариков станет вашим хобби, то без насоса не обойтись, ведь надувать их ртом – занятие нелегкое. Кроме того, шарики зачастую продаются без индивидуальной упаковки, поэтому контакт со слизистой рта может быть небезопасен. Самый доступный по цене вариант – двухходовый ручной насос. Несколько движений – и шарик надут. Если вам приходится надувать большое количество шаров, то стоит приобрести компрессор. Они выпускаются в двух вариациях: односпальные и двухспальные.
Как сделать собаку из шарика-колбаски
Твистинг – создание всевозможных фигур из воздушных шаров различной формы. Если раньше увидеть умельцев, складывающие продолговатые шарики в причудливые фигуры можно было только в парке аттракционов или цирке, то сегодня этим увлекательным делом может заняться каждый желающий. Технология их изготовления несложная, а необходимые материалы можно легко найти в продаже.
Полезные рекомендации
Для моделирования используются воздушные шары продолговатой формы. Наиболее удобными в работе считаются типы 260 или 260-2, которые отличаются эластичностью, крепостью и не лопаются во время надувания ртом.
Чтобы знать, как сделать из шарика собаку, нужно сначала освоить основные правила, без знания которых невозможно скрутить даже самую простую фигуру. Эти рекомендации будут особенно актуальными для тех, кто занимается подобным делом впервые:
- Перед надуванием нужно потянуть шар за кончики, чтобы он равномерно надувался и не лопнул в процессе.

- Надувать шарики нужно не полностью, оставляя хвостик в не надутом виде, чтобы иметь возможность сделать большее количество пузырей. Обычно в инструкции указывается необходимая длина хвостика.
- Начинающим любителям удобнее будет работать с изделиями из более мягких эластичных материалов.
- Завязывать кончик можно обычным узелком.
- Моделирование начинается от головы шарика (места завязанного узелка) чтобы оставить свободное место в районе его хвоста, где будет скапливаться лишний воздух.
- Перед закруткой нужно несколько раз сжать это место рукой, чтобы продвинуть лишний воздух.
- Закрутки нужно выполнять в одном направлении (к примеру, только к себе или, наоборот, от себя). Минимальный оборот для каждой скрутки – 360 градусов.
- Для надувания можно использовать специальные ручные компрессоры или проводить все манипуляции ртом.
Не стоит сразу приступать к сложным фигурам и пытаться смастерить необычный букет или человечка.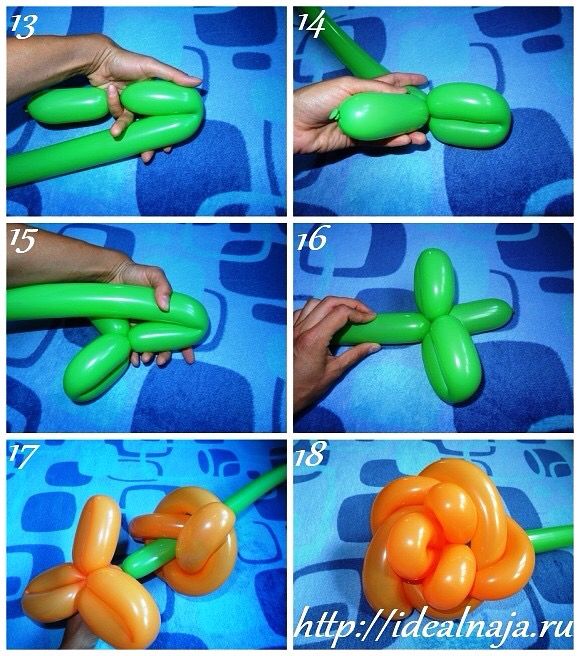 Чтобы приобрести необходимые навыки и понять основные принципы работы, лучше начинать с малого. Например, можно сделать из шарика колбаски собаку – одну из наиболее простых и популярных моделей в твистинге.
Чтобы приобрести необходимые навыки и понять основные принципы работы, лучше начинать с малого. Например, можно сделать из шарика колбаски собаку – одну из наиболее простых и популярных моделей в твистинге.
Инструкция по созданию собаки
Подробно узнать, как сделать собаку можно по представленной инструкции. Для этого необходимо иметь длинный шарик для моделирования, насос, немного времени и терпения. Для изготовления фигурки нитки не понадобятся. Весь процесс будет сопровождаться подробным описанием каждого этапа и фотографиями для лучшего понимания. Воспользовавшись приведенной схемой, можно без особых усилий смастерить красивую собачку.
Пошаговая схема
- Надуваем шарик, оставив хвостик длиной 8-10 см.
- Отступив, 7-9 сантиметров со стороны узелка, делаем несколько оборотов, чтобы получилось некое подобие сосиски. Это будет мордочка собаки.
- Аналогичным образом делаем еще один пузырек чуть меньшего размера (около 5 сантиметров).

- Далее сгибаем шарик как показано на фото и скручиваем вторую «сосиску» с остальным туловищем.
- Следующий шаг – формирование шеи. Для этого нужно сделать пузырек длиной 6-7 сантиметров.
- Чтобы получить лапы нужно сделать скрутку, как показано на фото.
- Сгибая полученные пузырьки делаем передние лапы.
- Далее выделяем непосредственно туловище, делая еще один длинный пузырек длиной около 10 см.
- Задние лапы делаем по примеру передних лап и следим, чтобы они были одинаковых размеров.
- Собачка из шарика колбаски готова! При желании можно взять маркер и нарисовать глазки.
Немного потренировавшись, можно добавлять разные части тела и изменять пропорции колбасок. Например, делая длинное тело и короткие лапы, можно получить милую таксу. А если сделать фигурке длинную шею, то получится жираф.
Еще один вид собаки из шарика:
Читайте также:
Как сделать свою фигурку Шаровые шарниры
Фигурки были любимой игрушкой детей с конца 1950-х годов 1. Сегодня фигурки стали больше, чем просто игрушками. Людям всех возрастов нравится собирать, продавать и даже создавать свои собственные фигурки. Одна из основных проблем для тех, кто создает фигурки, — сделать фигуру максимально реалистичной, а ключ — в том, чтобы суставы двигались свободно и естественно. Создавая свои собственные шаровые опоры фигурки, вы можете придать придаткам фигурки более естественное и неограниченное ощущение движения.
Отделите руку фигурки от туловища.
Используйте бритвенный нож, чтобы сбрить все старые стыки или выступающие куски пластика. Отшлифуйте места соединения на руке и туловище, пока они не станут плоскими и гладкими. Продолжайте бритье и шлифовать до тех пор, пока обе части не станут плотно прилегать друг к другу.
Продолжайте бритье и шлифовать до тех пор, пока обе части не станут плотно прилегать друг к другу.
Отметьте центр сустава на туловище, где будет крепиться рука. Отметьте центр соответствующей области на руке.
Просверлите отверстие диаметром 1/8 дюйма и глубиной 1/8 дюйма в отметке на туловище.Поместите в отверстие каплю суперклея.
Закрутите заостренный конец винта с круглой головкой диаметром 1/8 дюйма и длиной 1/2 дюйма в отверстие в торсе с помощью отвертки с крестообразным шлицем. Оставьте 1/8 дюйма винта торчащей.
Оберните пластилин вокруг головки и стержня винта, создавая сверху шар диаметром 1/4 дюйма. Скульптура должна напоминать леденец.
Добавляйте или удаляйте пластилин, пока скульптура не будет выступать из туловища на 1/4 дюйма. Убедитесь, что диаметр шара остается неизменным и составляет 1/4 дюйма.Дайте глине высохнуть в течение четырех часов. Это будет шаровая часть шарового шарнира.
Просверлите отверстие диаметром 3/16 дюйма в отметке на рычаге; это будет розетка. Сделайте гнездо для руки глубиной 3/32 дюйма.
Сделайте гнездо для руки глубиной 3/32 дюйма.
Нагрейте розетку с помощью термофена. Прижмите руку к туловищу, пока пластик еще горячий, и осторожно перемещайте руку вперед и назад, чтобы гнездо начало переходить в форму шара. Дайте пластику остыть в течение часа.
Сделайте разрез в верхней части плеча на руке.Сделайте прорезь той же ширины, что и стержень шара, и перемещайте рычаг вверх и вниз, убедившись, что стержень мяча зафиксирован в прорези. Эта прорезь позволит руке двигаться вверх и вниз по мячу, а не просто по кругу.
Снимите рычаг и закрасьте шар и внутреннюю часть гнезда, чтобы они соответствовали рисунку.
Нагрейте раструб с помощью нагревательного пистолета и прижмите руку к туловищу. Добавьте дополнительную глину для лепки, чтобы увеличить диаметр шара, если гнездо кажется слишком большим.
Повторите весь процесс для другой руки, обеих ног и головы, если хотите.
Наконечники
При сверлении гнезда просверливайте отверстия с шагом 1/16 дюйма или 1/32 дюйма и регулярно проверяйте положение руки к туловищу, пока вы не будете удовлетворены креплением. При необходимости всегда можно просверлить глубже. Большинство сверл имеют калибр, позволяющий устанавливать заданную глубину. Это пригодится при сверлении розетки. При сверлении фигурки используйте минимально возможную скорость сверления.Это поможет предотвратить прожиг пластика или просверливание.
При необходимости всегда можно просверлить глубже. Большинство сверл имеют калибр, позволяющий устанавливать заданную глубину. Это пригодится при сверлении розетки. При сверлении фигурки используйте минимально возможную скорость сверления.Это поможет предотвратить прожиг пластика или просверливание.
Предупреждения
Обязательно надевайте защитные очки при использовании дрели. Будьте осторожны с тепловым пистолетом и расплавленным пластиком, они могут сильно обжечь вас.
Новый эффективный показатель результативности в молодежном футболе
Abstract
Успех в различных футбольных навыках, таких как удары ногами, зависит от достигнутых двигательных способностей. Удар ногами — это фундамент футбола, который зависит от множества различных и сложных факторов (техника, взаимодействие между ногами и мячом, полет мяча и т. Д.). Следовательно, важно определить игроков, которые могут выполнять более быстрые удары ногами, используя как доминирующую, так и недоминантную ногу. В текущем исследовании изучались некоторые основные переменные, влияющие на скорость ударов ногами в футболе, и их отношение к успеху в молодежной футбольной академии. В исследовании приняли участие 119 игроков первого и второго дивизиона. Они были случайным образом разделены на возрастные группы (U-15, U-17 и U19) и статус команды (первая команда, резерв). Диагностическая способность различных тестов скорости удара мяча по выявлению различий между игроками первой команды и резервом среди разных возрастных категорий была рассчитана с использованием анализа рабочих характеристик приемника.Результаты показали, что игроки первой команды достигли лучших результатов по сравнению с резервными в каждой категории. Кроме того, различия были больше в возрастной группе U-15 и U-17, чем в возрастной группе U-19. В заключение, скорость удара мяча может быть одним из возможных инструментов идентификации для оценки успеха игроков в юношеском футболе.
В текущем исследовании изучались некоторые основные переменные, влияющие на скорость ударов ногами в футболе, и их отношение к успеху в молодежной футбольной академии. В исследовании приняли участие 119 игроков первого и второго дивизиона. Они были случайным образом разделены на возрастные группы (U-15, U-17 и U19) и статус команды (первая команда, резерв). Диагностическая способность различных тестов скорости удара мяча по выявлению различий между игроками первой команды и резервом среди разных возрастных категорий была рассчитана с использованием анализа рабочих характеристик приемника.Результаты показали, что игроки первой команды достигли лучших результатов по сравнению с резервными в каждой категории. Кроме того, различия были больше в возрастной группе U-15 и U-17, чем в возрастной группе U-19. В заключение, скорость удара мяча может быть одним из возможных инструментов идентификации для оценки успеха игроков в юношеском футболе.
Образец цитирования: Raa A, Kuvačić G, De Giorgio A, Sellami M, Ardigò LP, Bragazzi NL, et al. (2019) Скорость удара мяча: новый эффективный показатель результативности в молодежном футболе.PLoS ONE 14 (5):
e0217101.
https://doi.org/10.1371/journal.pone.0217101
(2019) Скорость удара мяча: новый эффективный показатель результативности в молодежном футболе.PLoS ONE 14 (5):
e0217101.
https://doi.org/10.1371/journal.pone.0217101
Редактор: Даниэль Буллоса, Колледж медицинских наук Университета Джеймса Кука, БРАЗИЛИЯ
Поступила: 20 февраля 2019 г .; Дата принятия: 3 мая 2019 г .; Опубликован: 17 мая 2019 г.
Авторские права: © 2019 Rađa et al. Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии указания автора и источника.
Доступность данных: Все соответствующие данные находятся в рукописи и ее файле вспомогательной информации.
Финансирование: Авторы не получали специального финансирования на эту работу.
Конкурирующие интересы: Авторы заявили об отсутствии конкурирующих интересов.
Введение
Футбол — это сложный вид спорта, успех которого зависит от различных переменных и факторов, включая физиологические способности и технические навыки [1], и среди них одним из наиболее важных является удары ногами [2].Совершенствование футбольной техники недавно было освещено в литературе с помощью новаторской методики обучения молодых игроков [3]. Футбол включает в себя различные взрывные движения, такие как удар и передача мяча, отбор мяча, падение, прыжок, старт и остановка [4].
Lago-Peñas et al. объектировано, что игроки, которые стреляют больше во время матча, имеют больше шансов на успех, чем другие, которые стреляют меньше [5]. Это делает разработку правильной механики стрельбы критически важной, а улучшение удара ногой чрезвычайно важно во время тренировки спортсменов.Однако навыки удара ногой — непростая задача. Для правильного выполнения они требуют высоких технических навыков [6]. Следует отметить, что большинство ударов ногами обычно выполняется ногами (удар с подъема или боковой удар ногой) [7,8].
Следует отметить, что большинство ударов ногами обычно выполняется ногами (удар с подъема или боковой удар ногой) [7,8].
Анализ динамического движения удара ногой показал, что боковой удар ногой более точен, тогда как удар с подъема ногой является наиболее быстрым в футболе [9,10]. Чтобы увеличить вероятность забитого мяча, игрок должен достичь максимально возможной скорости мяча, которая зависит от нескольких переменных, таких как скорость стопы (дистальный сегмент) при ударе, а также качество удара мяча о ногу [11– 14].Кроме того, желательно иметь хорошую технику ударов ногами обеими ногами (доминирующей и недоминантной [15]). Более того, если удар выполняется быстрее, менее вероятно, что у вратаря или игрока соперника будет достаточно времени, чтобы среагировать [16–18].
Родригес Лоренцо и др. [8] проанализировали существующую литературу о влиянии максимальных скорости удара по мячу в зависимости от возраста, пола, доминирования конечностей, продолжительности тренировки, уровня соревнований, игровой позиции и вариаций в технике удара ногой. В 15–19 лет схема ударов ногами достигается полностью (при максимальной скорости удара ногой = 80–103 км / ч) [2]. Скорость мяча значительно выше после удара доминирующей ногой по сравнению с недоминантной ногой у юных испытуемых (86 против , 74 км / ч), у любителей (77 против , 70 км / ч), до опытные футболисты (98 против ,86 км / ч) [9,15,19] и более разных типов ударов [15]. Уровень соревнования является фактором, влияющим на максимальную скорость удара мяча [20], вероятно, из-за влияния опыта.
В 15–19 лет схема ударов ногами достигается полностью (при максимальной скорости удара ногой = 80–103 км / ч) [2]. Скорость мяча значительно выше после удара доминирующей ногой по сравнению с недоминантной ногой у юных испытуемых (86 против , 74 км / ч), у любителей (77 против , 70 км / ч), до опытные футболисты (98 против ,86 км / ч) [9,15,19] и более разных типов ударов [15]. Уровень соревнования является фактором, влияющим на максимальную скорость удара мяча [20], вероятно, из-за влияния опыта.
Таким образом, цель настоящего исследования заключалась в следующем: a) определить максимальной скорости удара по мячу с доминирующей и недоминантной ногой для двух наиболее часто используемых ударов ногами (с подъемом и сбоку) среди сегодняшних различных возрастных категорий в футболе. и б) изучить различия в скорости удара ногой между игроками первой и запасной команды с использованием определенных методов.
Материалы и методы
Участников
Для участия в настоящем расследовании были привлечены сто девятнадцать участников мужского пола, играющих в молодежных футбольных лигах Хорватии. Письменное согласие на участие в этом исследовании было получено от родителей / опекунов субъекта после того, как они были тщательно проинформированы о цели, преимуществах и потенциальных рисках этого исследования. Формы согласия были специально одобрены «Этическим комитетом факультета кинезиологии» (Сплит, Хорватия). Этот комитет одобрил весь дизайн исследования, которое было проведено в соответствии с этическими стандартами Хельсинкской декларации 1964 года и последующих поправок к ней.
Письменное согласие на участие в этом исследовании было получено от родителей / опекунов субъекта после того, как они были тщательно проинформированы о цели, преимуществах и потенциальных рисках этого исследования. Формы согласия были специально одобрены «Этическим комитетом факультета кинезиологии» (Сплит, Хорватия). Этот комитет одобрил весь дизайн исследования, которое было проведено в соответствии с этическими стандартами Хельсинкской декларации 1964 года и последующих поправок к ней.
Критериями включения в исследование были: i) участие не менее 85% тренировок, ii) регулярное участие в предыдущих соревновательных сезонах, iii) наличие действующего спортивного медицинского сертификата и iv) состояние здоровья (отсутствие боли. или травмы) и не употреблять никаких наркотиков.Все игроки имели подписанные удостоверения личности хорватской федерации футбола, были полностью здоровы и были обследованы местным врачом-специалистом по спорту. Участники воздерживались от напитков, содержащих кофеин, в течение 24 часов и не ели в течение 2 часов перед тестированием, чтобы уменьшить любое возможное вмешательство в эксперимент.
Дизайн
Это исследование представляет собой перекрестное исследование с двумя основными целями: определить скорость удара по мячу с доминирующей и недоминантной ногой при двух типах футбольного удара и изучить различия между игроками разных возрастных категорий.Участники были разделены на разные возрастные группы (U-15, U-17 и U-19) и статус команды (первая команда, резерв). Игроки первой команды были определены как игроки в стартовом составе. Эффективное игровое время не учитывалось. Настоящее исследование проводилось в июне по окончании соревновательного сезона 2014/2015. Каждый участник завершил все испытания в один и тот же период времени дня тестирования и в одних и тех же климатических условиях (16–7 часов вечера, температура 25,6 ± 0,8 ° C и относительная влажность 36,3 ± 2,5%).Участников просили избегать любой стрессовой деятельности во время тестирования или между тренировками.
Процедуры
Антропометрические данные были измерены с помощью портативного ростометра (SECA, Лестер, Великобритания; для роста) и электронных весов (HD-351, Tanita, Arlington Heights, США; для массы тела) [21]. Протокол тестирования включал стандартную разминку в течение 45 минут (с целевым значением 50% от теоретической максимальной частоты сердечных сокращений [220-возраст в годах]). Разминка включала 10 минут бега трусцой с мячом и без мяча, а также 10 минут динамической растяжки с сильным акцентом на мышцы ног и живота.
В течение последних 15 минут, приближаясь к тестированию и в ознакомительных целях [8], участники пасовали и стреляли ногами с подъема и сбоку, используя поочередно доминирующую и недоминантную ногу. По мере разминки игроки постепенно увеличивали скорость удара ногой, а также расстояние удара ногой. Тестирование проходило на искусственной траве в сухую и теплую погоду, мяч размещался на 11-метровой площадке. Участники были одеты в собственные футбольные бутсы, и использовались мячи Jabulani Football (Adidas, Германия; 69.0 ± 0,2 см в окружности и 440 ± 0,2 г массой). Участники трижды бросили по мячу ногой с подъема и сбоку, используя доминирующую и недоминантную ногу, в качестве альтернативы, что в сумме дает 12 ударов. Самый быстрый толчок на для каждого типа / ноги был рассмотрен для дальнейшего анализа. Игрокам, выстроившимся за 11-метровой точкой, была дана инструкция бросить один за другим мяч как можно быстрее и прямо в центр ворот. После того, как каждый игрок стрелял по мячу, он подходил к концу линии, чтобы избежать любого потенциального влияния усталости.Таким образом, у каждого игрока было минимум 3 минуты между повторными ударами.
Во время испытаний был привлечен спортивный ученый для лучшего контроля и управления задачами. Он должен был дать указание: «Готово-сет-вперед», поэтому в «Иди» игрок начал разбегаться, в то время как другой спортивный ученый принимал меры с помощью карманного радара (Pocket Radar, Inc. Санта-Роза, Калифорния) с Точность ± 2 км / ч на расстоянии 1 м от ворот на высоте мяча во время удара [22].
Статистический анализ
Была рассчитана базовая описательная статистика, а именно как среднее значение или средний балл (AS), стандартное отклонение (SD), диапазон — минимум и максимум результатов (мин., Макс.) Для антропометрического статуса участников. Систематическая систематическая ошибка переменных эффективности удара определялась с помощью одностороннего дисперсионного анализа (ANOVA) для повторных измерений с апостериорным тестом Бонферрони для возможных значимых сравнений. Для относительной надежности коэффициент внутриклассовой корреляции (ICC) с 95% доверительным интервалом (95% CI) был рассчитан с помощью дисперсионного анализа как (MSB – MSW) / MSB, где MSB и MSW — это среднеквадратическая дисперсия между индивидуумом и внутри индивидуума, соответственно.Значения ICC менее 0,50, от 0,50 до 0,75, от 0,75 до 0,90 и более 0,90 указывают на низкую, среднюю, хорошую и отличную надежность соответственно [23]. Различия в скорости ударов ногой между первой командой и запасными определялись с помощью теста Стьюдента t с 95% доверительным интервалом для средних различий между группами. Чтобы оценить величину различий, была рассчитана величина эффекта Коэна. Пороговые значения для интерпретации размера эффекта были <0,25 (тривиально), 0.От 25 до 0,50 (маленький), от 0,50 до 1,0 (средний) и> 1,0 (большой) [24]. Диагностическая способность различных тестов скорости удара ногой по мячу (IKDL – доминирующая нога с подъемом стопы, SFKDL –– боковая нога ––––––––––––––––––––––––––––––––––– ––– нед –– –– недоминант –– нога) — для выявления различий между Были рассчитаны игроки первой команды и резервы среди разных возрастных категорий с помощью анализа рабочих характеристик приемника (ROC). Мы знали, что для удара ногой с подъема максимальная скорость удара мяча более важна, тогда как боковой удар ногой более подходит в случае требований к точности [8].Тем не менее, мы также учли боковой удар ногой и максимальную скорость удара по мячу, потому что мы предположили, что более высокая скорость удара по мячу может сделать даже боковой удар ногой более эффективным. Площадь под кривой (AUC) вычислялась вместе с ее 95% доверительным интервалом и стандартной ошибкой (SE) согласно методике Делонга [25]. Парные сравнения были выполнены с поправкой на множественные сравнения. Статистически значимыми считались цифры со значением P менее 0,05.Все статистические анализы проводились с использованием коммерческого программного обеспечения Statistica версии 13.0 (Dell Inc., Round Rock, TX USA).
Данные для таблиц в этой статье доступны в онлайн-материале (Таблица S1).
Результаты
Настоящее исследование включало 119 юных (средний возраст 16,20 ± 1,33 года) футболистов из первой и второй хорватской лиги пионеров (U-15, n = 32, 26,9% выборки), кадетов (U- 17; n = 51, 42,9%) и юниоры (U-19, n = 36, 30.3%).
Антропометрические данные представлены в таблице 1. Значения роста, массы и индекса массы соответствуют возрастной категории. Средние значения роста и массы для игроков U-15 были чуть ниже 75 -го -го процентиля (U-17 находились на 75--м процентиле ) в соответствии с американскими эталонными значениями [26,27]. Игроки участвовали в программе футбольных тренировок четыре раза в неделю и сыграли один соревновательный матч за неделю. Общий объем еженедельных тренировок / матчей для игроков U-15, U-17 и U-19 составил 7.1 ± 0,4 часа, 7,6 ± 0,5 часа, 8,5 ± 0,4 часа соответственно. В течение футбольного сезона футболисты активно тренировались в течение 44 недель.
Все 4 типа футбольных ударов имели значения ICC от умеренного до отличного (0,67–0,96), как показано в таблице 2. Максимальные пробные баллы были использованы для последующих анализов, за исключением U-15 SFKNL, где post-hoc сравнение с поправкой Бонферрони показало значительную разницу между тремя последовательными ударами по футболу (1 испытание против .2 испытание; P <0.01).
Скорость удара мяча среди разных возрастных категорий и различия между игроками первой команды и резервом показаны в Таблице 3. В возрастной категории до 15 лет, между игроками первой команды и запасными, результаты значительно различались между тремя группами футбольных ударов: ( IKDL, т = -3,86, P <0,01; SFKDL, т = -3,82, P <0,01; IKNL, т = -1,87, P = 0,07; и SFKNL, т = -2,75, P <0.05). Однако в U-17 значимые различия между группами были обнаружены во всех футбольных ударах (IKDL, t = -4,52, P <0,01; SFKDL, t = -2,41, P <0,05; IKNL, t = -4,94, P <0,01; и SFKNL, t = -2,43, P <0,05). Только IKDL ( t = -2,53, P <0,01) может различать основную команду и резерв в возрастной категории U-19, в то время как в других ударах мы не обнаружили существенных различий (SFKDL, t = -0.78, P = 0,44; ИКНЛ, т = -1,92, Р = 0,06; и СФКНЛ, t = -0,93, P = 0,36).
При сравнении всех футбольных ударов участники достигли максимальной скорости с IKDL (первая команда U-15 100,27 ± 4,76 км / ч против . Резерв 90,59 ± 8,61 км / ч; первая команда U-17 107,43 ± 4,65 км / ч vs . Запасы 100,86 ± 5,56 км / ч; и первая группа U-19 111,3 ± 4,35 км / ч против . Запасы 106,94 ± 6,15 км / ч), в то время как, как и ожидалось, самая низкая скорость была у SFKNL (первая группа U-15 команда 80.27 ± 6,69 км / ч против . запасы 71 ± 11,42 км / ч; Первая команда U-17 87,87 ± 7,58 км / ч против . запасы 82,82 ± 7,2 км / ч; и первая команда U-19 90,2 ± 6,07 км / ч против . запасы 88,13 ± 7,38 км / ч).
Что касается ROC-анализа, для U-15 AUC варьировала от 0,673 (IKNL) до 0,837 (SFKDL), тогда как для U-17 AUC варьировала от 0,680 (SFKDL) до 0,819 (IDKL), а для U-19. , AUC варьировала от 0,584 до 0,780. Более подробная информация представлена в таблице 4.
При попарном сравнении кривых ROC (рис.1) для U-15 ИДКЛ не отличался от ИКНЛ (Δ = 0.131 [95% ДИ -0,0861–0,349], SE = 0,111, z = 1,184, P = 0,2364), из SFKDL (Δ = 0,0333 [95% ДИ -0,0862–0,153], SE = 0,0610, z = 0,546, P = 0,5848), и из SFKNL (Δ = 0,0451 [95% ДИ -0,0952–0,185], SE = 0,0716, z = 0,630, P = 0,5287). Точно так же IKNL не отличался от SFKDL (Δ = 0,165 [95% ДИ -0,0466–0,376], SE = 0,108, z = 1,528, P = 0,1265) и от SFKNL (Δ = 0,0863 [95% ДИ — 0,125–0,298], SE = 0.108, z = 0,799, P = 0,4242). Наконец, SFKDL не отличался от SFKNL (Δ = 0,0784 [95% ДИ -0,0684–0,225], SE = 0,0749, z = 1,047, P = 0,2950).
Рис. 1. Анализ ROC с разбивкой по игрокам U-15, U-17 и U-19.
ИКДЛ — удар ногой в гору с доминирующей ноги; СФКДЛ — боковой удар доминирующей ногой; IKNL — недоминантная нога с подъемом на подъем; СФКНЛ — боковой удар недоминантной ногой.
https://doi.org/10.1371/journal.pone.0217101.g001
Для U-17 IDKL не отличался от IKNL (Δ = 0,0536 [95% CI -0,0838–0,191], SE = 0,0701, z = 0,764, P = 0,4448) и от SFKNL (Δ = 0,131 [95% ДИ -0,0365–0,299]], SE = 0,0855, z = 1,534, P = 0,1251), но отличается от SFKDL (Δ = 0,139 [95% ДИ 0,00826–0,270], SE = 0,0667, z = 2,084, P = 0,0372). IKNL отличался от SFKDL (Δ = 0,193 [95% ДИ 0,0351–0,350], SE = 0,0804, z = 2,396, P = 0.0166) и из SFKNL (Δ = 0,185 [95% ДИ 0,0437–0,326], SE = 0,0720, z = 2,566, P = 0,0103). Наконец, SFKDL не отличался от SFKNL (Δ = 0,00776 [95% ДИ -0,132–0,148], SE = 0,0713, z = 0,109, P = 0,9133).
Для U-19 IDKL отличался только от SFKDL (Δ = 0,195 [95% CI 0,0392–0,351], SE = 0,0796, z = 2,453, P = 0,0142), но не от IKNL (Δ = 0,0766 [ 95% ДИ -0,0805–0,234], SE = 0,0801, z = 0,956, P = 0.3392) и из SFKNL (Δ = 0,172 [95% ДИ -0,0265–0,370], SE = 0,101, z = 1,698, P = 0,0895). IKNL не отличался от SFKDL (Δ = 0,119 [95% ДИ -0,0927–0,330], SE = 0,108, z = 1,101, P = 0,2710) и от SFKNL (Δ = 0,0953 [95% ДИ -0,0734– 0,264], SE = 0,0861, z = 1,107, P = 0,2683). Наконец, SFKDL не отличался от SFKNL (Δ = 0,0234 [95% ДИ -0,155–0,202], SE = 0,0912, z = 0,257, P = 0,7972).
Обсуждение
Основными целями этого исследования было определение скорости удара ногой по мячу с доминирующей и недоминантной ногой для двух часто используемых футбольных ударов в разных возрастных категориях и определение различий в скорости удара по мячу между игроками первой и второй команд. В этом исследовании более успешные игроки (первая команда) достигли более высокой скорости мяча по сравнению с запасными. Глядя на результаты статистической значимости, различия были больше у игроков U-15 и U-17 по сравнению с категорией U-19.Величина различий между игроками первой команды и запасных была очень большой к большому (U-15), очень большим к среднему (U-17) и от большого к малому (U-19). Различия в скорости удара мяча между игроками основной команды и запасными, кажется, уменьшаются с возрастом.
Интересно, что фактические результаты отличались от предыдущих в многочисленных исследованиях, в которых измерялась эффективность ударов ногами по мячу без учета возрастных групп [16,28–30]. Иными словами, Родригес-Лоренцо и др.Исследование — с учетом меньшего числа возрастных групп — обеспечило скорость ударов ногами, аналогичную результатам текущего исследования [31]. Кроме того, в большинстве исследований измерялась скорость мяча при ударе ногой [28,29,32–34]. Насколько нам известно, существует только одно исследование, в котором оценивается скорость удара футболистов на разных уровнях соревнований [35], но в нем участвовало старших футболиста и не было обнаружено различий между 1-м и 2-м дивизионами и любителями. игроков.
Результаты AUC для ноги с доминирующим ударом с подъема для всех возрастных категорий были выше, чем для ноги с доминирующим ударом с подъема и с доминирующим и не доминирующим боковым ударом, и подтверждают, используя анализ ROC, существующую литературу, сообщающую, что максимальная скорость может в основном достигается при использовании доминирующей ноги и ударах ногами со шнурками [2,9,10].Этот вывод применим для всех возрастных категорий. С другой стороны, результаты AUC с преобладанием и недоминантностью бокового удара ногой были ниже во всех группах, особенно у пожилых, что подтверждает влияние возраста на скорость сокращения мышц с возрастом [36]. Такие результаты подтверждают, что они очень интересны, поскольку они намекают на то, что даже возможное обнаружение небольшого снижения скорости удара ногой в более возрастной группе (например, 17 против 900 44, 15 лет) должно быть принято во внимание.
Если рассматривать отдельно разные возрастные категории для игроков U-15 первой и резервной команды, то скорость удара по мячу, достигнутая с помощью IKDL, лучше, чем у Marques et al. (100,3 км / ч и 87,7 км / ч против , 84,6 км / ч [37]). Для игроков U-17 существует множество вариаций результатов IKDL. Хуарес и др. [28] сообщили о скорости 108,22 км / ч, что аналогично скорости, полученной игроками U-17 из первой команды в этом исследовании, но лучше, чем результат, достигнутый резервом.Nunome et al. [38] у элитных игроков U-17 скорость удара ногой составила 115,6 км / ч, тогда как более низкие оценки были получены в исследованиях Tomáš et al. [29] и Гарсия-Пинильос и др. [34], 102,89 км / ч и 84,85 км / ч соответственно. Удар ногами в футболе — чрезвычайно важная часть игры, и в молодежных академиях часто рассматривается как один из ключевых факторов, определяющих качество и отбор талантов. Игроки первой команды наносили более быстрые удары, чем резервные для всех возрастных категорий, и различия были статистически значимыми и намного выше среди игроков U-15 и U-17.Можно отметить, что различия в скорости ударов ногами между игроками первой команды и резервными имеют тенденцию уменьшаться с возрастом. Эти результаты могут быть индикатором влияния некоторых других переменных, лежащих в основе игры игроков. Возможной причиной этого может быть разница во времени скачка роста и созревания среди мальчиков. Игроки, которые биологически развиваются раньше, часто выбираются в более успешные команды и в первые команды [39–48]. Подтверждено, что из-за различий в биологическом статусе более зрелые игроки имеют большую мышечную массу и могут генерировать больше мощности и ускорения на концах конечностей и достигать более быстрых ударов ногами.Такой вывод предполагает, что оценка скорости ударов ногами в старших возрастных категориях не имеет особого смысла, поскольку выполняется после набора тренеров и тренеров с учетом относительного возрастного эффекта и биологического статуса , что делает пожилых игроков более однородными с точки зрения скорости ударов ногами [48] . С другой стороны, оценка скорости ударов ногами в младших возрастных категориях может иметь определенный смысл, потому что она может лучше выявить реальные различия между молодыми игроками, еще не затронутыми будущими тренировками тренеров и тренеров (и, следовательно, в выборке, более неоднородной с точки зрения навыков) [31] .В категории U-19 только при ударе с подъема доминирующей ногой наблюдалась статистически значимая разница между игроками первой и второй команд. Такие результаты могут быть показателем того, как различия уменьшаются по мере приближения к старшему / профессиональному статусу игроков. С возрастом выбор игроков становится больше, поэтому различий между игроками первой и резервной команды становится меньше. Скорость ударов ногами в футболе потенциально может быть одним из показателей эффективности и инструментом отбора в молодежном футболе, особенно в более молодом возрасте, но ее необходимо оценивать с учетом нескольких других аспектов ( в primis , биологический статус ).
Ограничением этого исследования было то, что мы использовали слишком длительную разминку (45 минут) для протокола ударов ногами. Более короткая 10-минутная разминка плюс 5-минутная активная растяжка была бы более подходящей для нашего протокола [2]. Еще одно ограничение заключалось в том, что мы не проверяли наличие признаков утомляемости (например, путем постоянного мониторинга частоты сердечных сокращений игроков) во время администрирования протокола. Другой способ контролировать наступление утомления — позволить каждому игроку определять свой собственный темп в соответствии с протоколом [20].
Выводы
Для юных игроков разных возрастных категорий были обнаружены статистически значимые различия в скорости удара по мячу при ударах подъемом и боковыми ногами с доминирующей и недоминантной ногой между основной и резервной командой. В этом исследовании самым быстрым ударом ногой была стопа с доминирующей ногой, а самым медленным — боковой ногой с не доминирующей ногой. Кроме того, в группах U-15 и U-17 можно было обнаружить существенные различия между первой командой и резервом по сравнению со старшей группой U-19.Предыдущие исследования, кажется, предполагают влияние определенных биологических факторов, таких как скачок роста и созревание, на выбор в первую команду. Удары ногами в футболе могут быть показателем качества для оценки навыков игроков в футбол. Оценивая результативность футбольных ударов ногами, можно быстро, легко и эффективно получить соответствующие результаты, которые могут быть использованы в процессе отбора молодых футболистов.
Благодарности
Авторы благодарят всех специалистов, врачей и футболистов за участие в экспериментальной работе.
Ссылки
- 1. Келлис Э., Катис А. Биомеханические характеристики и детерминанты футбольного удара с подъемом. J Sports Sci Med. 2007. 6: 154–165. pmid: 24149324
- 2. Бакваревич Б.Б., Пазин Н., Божич П., Мирков Д., Куколь М., Ярич С. Оценка результатов комплексного теста на результативные удары ногами. J Strength Cond Res. 2012; 26: 1945–1952. pmid: 22728945
- 3. Де Джорджио А., Селлами М., Кувачич Дж., Лоуренс Дж., Падуло Дж., Мингарди М. и др.Улучшение моторного обучения юных футболистов за счет предотвращения внутренней фокусировки внимания: Влияние цвета обуви. PLoS One. 2018; 13: e0200689. pmid: 30110332
- 4. Рейли Т., Уильямс А.М., Невилл А., Фрэнкс А. Междисциплинарный подход к выявлению талантов в футболе. J Sports Sci. 2000. 18: 695–702. pmid: 11043895
- 5. Лаго-Пеньяс С., Лаго-Баллестерос Дж. Местоположение игры и качество команды влияют на профили результатов в профессиональном футболе.J Sports Sci Med. 2011; 10: 465–471. pmid: 24150619
- 6. Лис А., Асаи Т., Андерсен Т. Б., Нуном Х, Стерзинг Т. Биомеханика удара ногой в футболе: обзор. J Sports Sci. 2010. 28: 805–817. pmid: 20509089
- 7. Simiyu WW. Анализ голов, забитых на чемпионате мира по футболу 2010 года в ЮАР. Журнал физического воспитания и спорта. 2013; 13: 6–13.
- 8. Родригес Лоренцо Л., Фернандес-Дель-Олмо М., Асеро Р. Критический обзор параметров техники и примерных характеристик максимальной скорости удара ногами в футболе.Strength Cond J. 2015; 37: 26–39.
- 9. Нуномэ Х, Асаи Т., Икегами Й, Сакураи С. Трехмерный кинетический анализ футбольных ударов ногой сбоку и подъемом. Медико-спортивные упражнения. 2002; 34: 2028–2036. pmid: 12471312
- 10. Арпинар-Авсар П, Сойлу АР. Согласованность в схемах ускорения футболистов разного уровня подготовки. J Sports Sci Med. 2010. 9: 382–387. pmid: 24149630
- 11. Асаи Т., Карре MJ, Акацука Т., Хааке SJ. Кривой удар футбольного мяча I: удар ногой.Sports Eng. 2002; 5: 183–192.
- 12. Андерсен ТБ, Дорхе, Томсен. Столкновения при ударах по футболу. Sports Eng. 1999; 2: 121–125.
- 13. Лис А., Нолан Л. Биомеханика футбола: обзор. J Sports Sci. 1998. 16: 211–234. pmid: 9596356
- 14. Леванон Дж., Дапена Дж. Сравнение кинематики ударов с подъема и паса в футболе. Медико-спортивные упражнения. 1998. 30: 917–927. pmid: 9624652
- 15. Маклин Б.Д., Тумилти Д.М.Асимметрия слева направо в двух типах футбольного удара. Br J Sports Med. 1993. 27: 260–262. pmid: 8130965
- 16. Дёрге ХК, Андерсен ТБ, Сёренсен Х., Симонсен Е.Б. Биомеханические различия в ударах футболиста с предпочтительной и нежелательной ногой. J Sports Sci. 2002; 20: 293–299. pmid: 12003274
- 17. Маркович Г., Диздар Д., Ярич С. Оценка тестов на максимальную эффективность ударов ногами. J Sports Med Phys Fitness. 2006. 46: 215–220. pmid: 16823350
- 18.Синклер Дж., Фьютрелл Д., Тейлор П.Дж., Аткинс С., Боттомс Л., Хоббс С.Дж. Трехмерные кинематические различия между предпочтительными и нежелательными конечностями во время максимального футбольного удара ногой с подъема. J Sports Sci. 2014; 32: 1914–1923. pmid: 25333601
- 19. Барфилд В. Биомеханика ударов ногами в футболе. Clin Sports Med. 1998. 17: 711–728. pmid: 9922896
- 20. Шан Г. Влияние пола и опыта на максимальный футбольный удар с подъемом. Eur J Sport Sci.2009; 9: 107–114.
- 21. De Siati F, Laffaye G, Gatta G, Dello Iacono A, Ardigò LP, Padulo J. Нервно-мышечные и технические способности игроков в водное поло, связанные с возрастом. J Sports Sci. 2016; 34: 1466–1472. pmid: 26643977
- 22. ван ден Тиллаар Р., Ульвик А. Влияние инструкций на скорость и точность ударов ногами опытных футболистов. J Mot Behav. 2014; 46: 287–291. pmid: 24773185
- 23. Ку ТК, Ли МЫ. Руководство по выбору и сообщению коэффициентов внутриклассовой корреляции для исследования надежности.J Chiropr Med. 2016; 15: 155–163. pmid: 27330520
- 24. Рея MR. Определение величины лечебного эффекта в исследованиях силовых тренировок с использованием величины эффекта. J Strength Cond Res. 2004; 18: 918–920. pmid: 15574101
- 25. Делонг ER, Делонг DM, Кларк-Пирсон DL. Сравнение площадей под двумя или более коррелированными кривыми рабочих характеристик приемника: непараметрический подход. Биометрия. 1988; 44: 837–845. pmid: 3203132
- 26.Дьюи К.Г., Пирсон Дж. М., Браун К. Х., Кребс Н. Ф., Михаэльсен К. Ф., Перссон Л. А. и др. Рост детей, находящихся на грудном вскармливании, отклоняется от текущих справочных данных: объединенного анализа наборов данных из США, Канады и Европы. Рабочая группа Всемирной организации здравоохранения по росту младенцев. Педиатрия. 1995; 96: 495–503. pmid: 7651784
- 27. Малина Р.М., Бушар С., Бар-Ор О. Рост, созревание и физическая активность. Шампанское: Human Kinetics; 2004.
- 28. Хуарес Д., Лопес де Субихана С., Малло Дж., Наварро Э.Острое влияние упражнений на выносливость на прыжки и удары ногами у лучших юных футболистов. Eur J Sport Sci. 2011; 11: 191–196.
- 29. Томаш М., Франтишек З., Люсия М., Ярослав Т. Профиль, соотношение и структура скорости у юных элитных футболистов. J Hum Kinet. 2014; 40: 149–159. pmid: 25031683
- 30. Маркович Г., Диздар Д., Ярич С. Оценка тестов на максимальную эффективность ударов ногами. J Sports Med Phys Fitness. 2006. 46: 215–220. pmid: 16823350
- 31.Родригес-Лоренцо Л., Ольмо Ф. Д., Санчес-Молина Х. А., Мартин-Асеро Р. Способность к ударам ногой и дефицит ударов ногами у молодых элитных футболистов. Kinesiol Int J Fundam Appl Kinesiol. 2018; 50: 80–82.
- 32. Амири-Хорасани М., Абу Осман Н.А., Юсоф А. Биомеханические реакции бедра и голени во время 10 последовательных футбольных ударов ногой. J Strength Cond Res. 2011; 25: 1177–1181. pmid: 20838249
- 33. Белица Д., Попович С., Петкович Дж. Сравнение ударов ногой между предпочтительной и нежелательной стадиями у юных футболистов.Monten J Sports Sci Med 2013; 2: 5–10.
- 34. Гарсиа-Пинильос Ф., Мартинес-Амат А., Хита-Контрерас Ф., Мартинес-Лопес Э. Дж., Латорре-Роман, Пенсильвания. Влияние контрастной программы тренировок без внешней нагрузки на вертикальный прыжок, скорость удара, спринт и ловкость юных футболистов. J Strength Cond Res. 2014; 28: 2452–2460. pmid: 24626140
- 35. Кометти Дж., Маффиулетти Н.А., Пуссон М., Чатард Дж. К., Маффулли Н. Изокинетическая сила и анаэробная сила французских футболистов-элитных, субэлитных и любительских футболистов.Int J Sports Med. 2001; 22: 45–51. pmid: 11258641
- 36. Маккиннон Н.Б., Коннелли Д.М., Райс К.Л., Хантер С.З., Доэрти Т.Дж.. Нервно-мышечный вклад в возрастное снижение мышечной силы: механизмы и потенциальная роль высокоскоростной силовой тренировки. Издание Aging Res Rev.2017; 35: 147–154. pmid: 27697547
- 37. Маркес М.К., Перейра А., Рейс И.Г., ван ден Тиллар Р. Улучшает ли сезонная 6-недельная комбинированная тренировочная программа по спринту и прыжкам сила-скорость и результативность у молодых футболистов? J Hum Kinet.2013; 39: 157–166. pmid: 24511351
- 38. Нуномэ Х., Икегами Й., Козакаи Р., Априантоно Т., Сано С. Сегментарная динамика ударов ногой по футбольному подъему предпочтительной и нежелательной ногой. J Sports Sci. 2006; 24: 529–541. pmid: 16608767
- 39. Малина Р.М., Пенья Рейес М.Э., Эйзенманн Дж. К., Орта Л., Родригес Дж., Миллер Р. Рост, масса и скелетная зрелость элитных португальских футболистов в возрасте 11–16 лет. J Sports Sci. 2000. 18: 685–693. pmid: 11043894
- 40.Чибане С., Отье С., Гаудино С., Массарелли Р., Мимуни Н. Влияние возраста, зрелости и размеров тела на выбор алжирских футболистов до 17 лет. Наука и футбол VI. 2008; 125.
- 41. Чуман К., Хошикава Т., Иида Т., Секин С., Огава К., Накацука Ю. и др. 1 Тест на периодическое восстановление уровня 2 йо-йо для футболистов зрелого возраста в зависимости от категории зрелости. Возраст (лет). 2009; 7: 8.
- 42. Фигейредо AJ, Gonçalves CE, Coelho e Silva MJ, Malina RM.Характеристики юных футболистов, которые бросают учебу, упорствуют или продвигаются вверх. J Sports Sci. 2009. 27: 883–891. pmid: 19629837
- 43. Вонг Д.П., Вонг Ш. Физиологический профиль азиатских элитных юных футболистов. J Strength Cond Res. 2009; 23: 1383–1390. pmid: 19620928
- 44. le Gall F, Carling C, Williams M, Reilly T. Антропометрические и фитнес-характеристики международных, профессиональных и любительских футболистов мужского пола из элитной молодежной академии.J Sci Med Sport. 2010; 13: 90–95. pmid: 18835220
- 45. Малина Р.М., Пенья Рейес М.Э., Фигейредо А.Дж., Коэльо Э. Сильва М.Дж., Орта Л., Миллер Р. и др. Скелетный возраст у юных футболистов: значение для проверки возраста. Clin J Sport Med. 2010. 20: 469–474. pmid: 21079444
- 46. Мейлан С., Кронин Дж., Оливер Дж., Хьюз М. Идентификация талантов в футболе: роль статуса зрелости в физических, физиологических и технических характеристиках. Международный научный тренер по спортивным наукам. 2010; 5: 571–592.
- 47. Северино В., Гонсалвес Р.Р., Сильва М.Дж., Фигейредо А.Дж. Анналы исследований в области спорта и физической активности. 2011; 1: 36–52.
- 48. Raa A, Padulo J, Jelaska I, Ardigò LP, Fumarco L. Эффект относительного возраста и вторые уровни: нет второго шанса для игроков, родившихся позже. PLoS One. 2018; 13: e0201795. pmid: 30089178
Топология и комбинаторика футбольных мячей
С началом проводимого этим летом чемпионата мира по футболу, который проводится раз в четыре года, более миллиарда человек во всем мире обнаруживают, что экраны телевизоров и компьютеров заполнены изображениями футбольных мячей.В Германии, где проходят матчи чемпионата мира по футболу, футбольные мячи появляются на самых разных товарах, большая часть которых не имеет ничего общего с футболом.
Хотя футбольный мяч можно собрать по-разному, есть один дизайн, настолько распространенный, что он стал культовым. Этот стандартный футбольный мяч сшит или склеен из 32 многоугольников, 12 из которых пятисторонние и 20 шестигранных, расположенных таким образом, что каждый пятиугольник окружен шестиугольниками.Несмотря на постмодернистские раскраски, традиционный способ раскрасить такой шар — это покрасить пятиугольники в черный цвет, а шестиугольники — в белый. Сообщается, что эта цветовая схема была представлена на чемпионате мира в 1970 году, чтобы сделать мяч более заметным на телевидении, хотя сам дизайн более старый.
У большинства людей изображение футбольного мяча ассоциируется с часами, проведенными на поле или вне игры, или, возможно, просто с рекламой спортивных товаров. Но для математика футбольный мяч — интригующая головоломка.Почему это выглядит именно так? Есть ли другие способы собрать это вместе? Можно ли расположить пятиугольники и шестиугольники по-другому? Можно ли использовать другие многоугольники вместо пятиугольников и шестиугольников? Эти вопросы можно решить, используя язык математики — в частности, геометрию, теорию групп, топологию и теорию графов. Каждый из этих предметов дает концепции и естественный контекст для постановки вопросов, например, о конструкции футбольных мячей, а иногда и для ответов на них.
Важным аспектом применения математики является то, что разные способы математического понимания повседневных вопросов приводят к различным ответам. Это может стать сюрпризом для читателей, привыкших к школьным задачам, на которые есть только один правильный ответ. Правильная постановка вопросов — такая же важная часть искусства математики, как и ответы на них. Более того, подлинное математическое исследование открытого вопроса не ограничивается поиском «ответа» (если он есть), но предполагает понимание того, почему ответ такой, какой он есть, и как он изменяется при изменении лежащих в основе предположений.Вопросы, связанные с дизайном футбольных мячей, служат прекрасной иллюстрацией этого процесса.
Математики любят начинать с определения своих терминов. Что же такое футбольный мяч? Официальный футбольный мяч, который должен быть одобрен Международной федерацией футбольных ассоциаций (ФИФА), должен быть сферой с окружностью от 68 до 70 сантиметров, с отклонением от сферичности не более 1,5% при накачивании до давления 0,8 атмосферы.
Увы, такое определение ничего не говорит о том, как устроен шар, и поэтому не подходит для математического исследования конструкции.Лучшее определение: футбольный мяч — это примерно сфера, состоящая из многоугольников, или то, что математики называют сферическим многогранником . Места, где сходятся многоугольники — вершины и ребра многогранника — составляют карту на сфере, которая называется графом . (Такой график не имеет ничего общего с графиками функций. Слово имеет два совершенно разных математических значения.) Если рассматривать стандартный футбольный мяч с точки зрения теории графов, он имеет три важных свойства:
(1) это многогранник. состоящий только из пятиугольников и шестиугольников;
(2) стороны каждого пятиугольника пересекаются только с шестиугольниками; и
(3) стороны каждого шестиугольника поочередно пересекаются пятиугольниками и шестиугольниками.
В качестве отправной точки мы можем определить футбольный мяч как любой сферический многогранник со свойствами (1), (2) и (3). Если пятиугольники окрашены в черный цвет, а шестиугольники окрашены в белый цвет, то определение действительно захватывает иконическое изображение, хотя оно не определяет его однозначно.
Это определение помещает проблему дизайна футбольного мяча в контекст теории и топологии графов. Топология, часто описываемая как «геометрия резинового листа», представляет собой раздел математики, изучающий свойства объектов, которые не меняются в результате непрерывных деформаций, таких как надувание футбольного мяча.С точки зрения топологии не имеет значения, какова длина ребер многогранника, и имеем ли мы дело с круглым многогранником или многогранником с плоскими сторонами.
Я впервые столкнулся с указанным выше определением в 1983 году в задаче, поставленной на Bundeswettbewerb Mathematik, немецком математическом конкурсе для старшеклассников. Проблема заключалась в следующем: учитывая свойства (1) — (3), определить, из скольких пятиугольников и шестиугольников состоит футбольный мяч. Обдумывая эту проблему в то время, я предположил, что шар представляет собой выпуклый многогранник в пространстве, состоящий из правильных многоугольников.Это геометрическое предположение вместе с правилами (1), (2) и (3) подразумевает, что существует 12 пятиугольников и 20 шестиугольников. Более того, существует уникальный способ собрать их вместе, что дало начало культовому стандартному футбольному мячу. Без геометрического предположения проблема теории графов имеет бесконечно много других решений, которые имеют большее количество пятиугольников и шестиугольников.
Я снова начал думать об этой проблеме после того, как меня пригласили прочитать лекцию на церемонии награждения того же конкурса в 2001 году.В конце концов, один из моих докторантов, Фолькер Браунгардт, и я нашли способ охарактеризовать все решения, характеристику, которую я опишу ниже.
Интересно, что похожая проблема возникла в химии в 1980-х годах после открытия молекулы углерода из 60 атомов, названной бакминстерфуллереном или «бакиболом». Пространственная форма этой молекулы C 60 идентична стандартному многограннику футбольного мяча, состоящему из 12 пятиугольников и 20 шестиугольников, с 60 атомами углерода, размещенными в вершинах, и ребрами, соответствующими химическим связям.Открытие бакибола, которое было удостоено Нобелевской премии по химии 1996 г., вызвало огромный интерес к классу молекул углерода, называемых фуллеренами, которые удовлетворяют предположению (1) выше вместе с дополнительным условием:
(3 ‘) ровно три ребра пересекаются в каждой вершине.
Это свойство обусловлено химическими связующими свойствами углерода. Кроме того, предположение (2) иногда применяется для определения ограниченного класса фуллеренов. Ожидается, что наличие непересекающихся пятиугольников связано с химической стабильностью фуллеренов.Существует бесконечно много фуллереновых многогранников — C 60 был просто первым, который был обнаружен как настоящая молекула, — и весьма примечательно, что два бесконечных семейства многогранников, футбольные мячи и фуллерены, имеют только стандартный футбольный мяч. . Таким образом, (1) — (3) вместе с (3 ¢) дают уникальное описание стандартного футбольного мяча без каких-либо геометрических предположений. (Предположения, подобные регулярности, на самом деле подразумевают условие (3 ¢).)
Чтобы убедиться в этом, требуется краткий экскурс в свойства многогранников, начиная с красивой формулы, открытой швейцарским математиком Леонардом Эйлером в 18 веке.Формула Эйлера (см. «Формулу Эйлера» ниже ), основной инструмент теории графов и топологии, говорит, что в любом сферическом многограннике количество вершин v минус количество ребер e, плюс количество граней f равно 2:
v — e + f = 2
Применим формулу Эйлера к многограннику, состоящему из b черных пятиугольников и w белых шестиугольников.Общее количество f граней составляет b + w . Всего у пятиугольников 5b ребер, потому что на каждый пятиугольник приходится 5 ребер, а всего — b пятиугольника. Точно так же шестиугольники имеют в общей сложности 6w ребра. Сложение этих двух чисел должно дать общее количество ребер, за исключением того, что я посчитал каждое ребро дважды, потому что каждое ребро лежит на двух разных гранях. Для компенсации я делю на 2, и, следовательно, количество ребер равно:
e = (1/2) ( 5b + 6w )
Наконец, чтобы подсчитать количество вершин, я замечаю, что у пятиугольников всего 5b вершин, а у шестиугольников 6w вершин.В случае фуллерена предположение (3 ¢) говорит, что каждая вершина принадлежит трем разным граням. Таким образом, если я вычисляю 5b + 6w , я посчитал каждую вершину ровно три раза, и, следовательно, я должен разделить на 3, чтобы компенсировать:
v = (1/3) ( 5b + 6w )
Подставляя эти значения для f, e и v в формулу Эйлера, я обнаружил, что члены, включающие w , сокращаются, и формула сокращается до b = 12.Следовательно, каждый фуллерен содержит ровно 12 пятиугольников! Однако не существует априорного ограничения на количество шестиугольников, w , и, следовательно, нет ограничения на количество вершин. (Это подразумевается в названии статьи 1997 года о фуллеренах в American Scientis t: «Фуллереновые нанотрубки: C 1,000,000 и не только».) Если я наложу дополнительное условие (2), то я смогу показать, что число шестиугольников должно быть не менее 20. Стандартный футбольный мяч или бакибол реализует это минимальное значение, для которого количество вершин v равно 60, что соответствует 60 атомам в молекуле C 60 .Однако можно показать, что действительно существует бесконечно много других математических возможностей для фуллереновидных многогранников. Какие из них соответствуют реальным молекулам, является предметом исследования в химии.
Формула Эйлера
Любой непустой связный конечный граф на сфере удовлетворяет формуле Эйлера v — e + f = 2. Здесь v и e — количество вершин и ребер, а f — число вершин и ребер. количество регионов, на которые разделена сфера.Доказательство формулы Эйлера проводится путем многократного упрощения графа с помощью следующих двух операций:
Первая операция состоит из удаления любой вершины, которая встречается только с одним ребром, и, кроме того, удаления ребра, которое встречается с ней ( a, на изображении ниже ). Эта операция не изменяет количество областей, но уменьшает как v , так и e на 1. Вторая операция состоит в сворачивании области в одну вершину вместе со всеми ребрами и вершинами на ее границе ( b ).Если сжатая область имеет k вершин на своей границе, то это сжатие уменьшает v на k -1, уменьшает e на k и уменьшает f на 1. Таким образом, v — e + f не изменяется ни одной из двух операций.
Конечная итерация этих двух упрощений сводит любой граф к графу только с одной вершиной и без ребер. Тогда есть одна область, и v — e + f = 1 — 0 + 1 = 2.
Для футбольных мячей нам разрешено использовать только допущения (1) — (3), но не (3 ¢), требование химика-угольника о том, что три ребра пересекаются в каждой вершине. В этом случае количество граней, пересекающихся в вершине, не фиксировано, но это число равно не менее 3. Следовательно, уравнение v = (1/3) ( 5b + 6w ) становится неравенством y: v £ (1/3) ( 5b + 6w ). Подставляя в формулу Эйлера, члены, содержащие w , снова сокращаются, оставляя неравенство b ³ 12.Таким образом, каждый футбольный мяч содержит не менее 12 пятиугольников, но, в отличие от фуллерена, может содержать и больше.
Также, в отличие от фуллеренов, футбольные мячи имеют точное соотношение между числом пятиугольников и числом шестиугольников. Подсчитывая количество ребер, вдоль которых встречаются пятиугольники и шестиугольники, условие (2) говорит, что все ребра пятиугольников также являются ребрами шестиугольников, а условие (3) говорит, что ровно половина ребер шестиугольников также являются ребрами пятиугольников. Следовательно, (1/2) ( 6w ) = 5b или 3w = 5 b.Поскольку b ³ 12, w равно минимум 20. Эти минимальные значения реализуются стандартным футбольным мячом, и реализация комбинаторно уникальна из-за условий (2) и (3). Но существует также бесконечно много других численных решений, и возникает проблема, соответствуют ли эти неминимальные численные решения многогранникам футбольного мяча. Оказывается, да, как мы вскоре увидим, так что действительно существует бесконечная коллекция футбольных мячей.
Таким образом, мы видим, что существует бесконечно много фуллеренов (удовлетворяющих предположениям (1), (2) и (3 ¢)) и бесконечно много футбольных мячей (удовлетворяющих (1), (2) и (3)). Однако, если мы объединим два определения, есть только одна возможность! Для фуллерена b = 12, а для футбольного мяча 5b = 3w . Следовательно, чтобы футбольный мяч также был фуллереном, мы должны заключить, что 5 ´ 12 = 3w, или w = 20. Следовательно, любой футбольный мяч, который также является фуллереном, должен иметь 12 пятиугольников и 20 шестиугольников.Известно, что существует 1812 различных фуллеренов с 12 пятиугольниками и 20 шестиугольниками, но 1811 из них имеют где-то смежные пятиугольники и поэтому не являются футбольными мячами, поскольку нарушают условие (2). Стандартный футбольный мяч — единственный, у которого нет прилегающих пятиугольников.
Оставив позади химию и графы фуллеренов, давайте теперь рассмотрим ключевой вопрос: какие еще существуют нестандартные футбольные мячи, у которых более трех граней встречаются в какой-то вершине, и как мы можем их понять? Оказывается, мы можем сгенерировать бесконечные последовательности различных футбольных мячей с помощью топологической конструкции, называемой разветвленным покрытием в g.Вы можете визуализировать это, представив стандартный рисунок футбольного мяча, наложенный на поверхность Земли и выровненный так, чтобы одна вершина находилась на Северном полюсе, а другая — на Южном полюсе. Теперь искажайте узор так, чтобы один из зигзагообразных путей по краям от полюса к полюсу выпрямлялся и лежал на меридиане, скажем, нулевом меридиане нулевой географической долготы (см. Рис. 4b ). График можно искажать, потому что мы делаем «резиновую геометрию».
Затем представьте, что Земля разрезается вдоль нулевого меридиана. Сжимайте разрезанный слой Земли в направлении восток-запад, удерживая полюса фиксированными, до тех пор, пока покрытие не покроет ровно половину сферы, скажем, Западное полушарие. Наконец, возьмите копию этого сморщенного пальто и поверните его вокруг оси север-юг, пока она не покроет Восточное полушарие. Примечательно, что эти две части можно сшить вместе, что придает сфере новую структуру футбольного мяча с вдвое большим количеством пятиугольников и шестиугольников, чем раньше.Причина в том, что на каждом из двух швов, проходящих между Северным и Южным полюсами, две стороны шва неотличимы от двух сторон разреза, который мы сделали в нашем оригинальном футбольном мяче. Таким образом, эти две части идеально подходят друг к другу таким образом, что условия смежности (2) и (3) сохраняются. (Пошаговые иллюстрации этой конструкции см. На Рисунке 4.)
Новый футбольный мяч, построенный таким образом, называется двояко разветвленным, покрывая исходного, а полюса называются точкой ветвления с.Новый шар выглядит так же, как старый (с точки зрения топологии или геометрии резинового листа), за исключением точек ветвления. Теперь есть шесть граней (вместо трех), пересекающихся в этих двух вершинах, и есть 116 других вершин (58 вершин, которые не были закреплены на полюсах, плюс их дубликаты), при этом по три грани встречаются в каждой из них.
Мы можем внести в эту конструкцию простую модификацию. Вместо того чтобы брать двукратные покрытия, мы можем взять d -кратно разветвленные накрытия для любого натурального числа d .Вместо того, чтобы сжимать сферу наполовину, мы представляем апельсин, состоящий из d оранжевых секций, и для каждой секции мы сжимаем копию покрытия сферы так, чтобы она точно помещалась над секцией. Еще раз разные части соединяются по швам (см. Рисунок 5) . Для всего этого важно, чтобы мы думали о футбольных мячах как о комбинаторных или топологических, а не геометрических объектах, так что многоугольники могут быть искажены произвольно.
На этом этапе вы можете подумать, что может быть гораздо больше примеров футбольных мячей, возможно, созданных из стандартного с помощью других модификаций, или, возможно, единичные примеры, не имеющие очевидной связи со стандартным футбольным мячом.Но это не так! Мы с Браунгардтом доказали, что каждый футбольный мяч на самом деле является подходящим разветвленным покрытием стандартного (возможно, с немного более сложным ветвлением, чем обсуждалось выше).
Доказательство включало интересное взаимодействие между локальной структурой футбольных мячей вокруг каждой вершины и глобальной структурой разветвленных покрытий. Рассмотрим любую вершину любого футбольного мяча (см. Рис. 6 ). Для каждой грани, пересекающейся с этой вершиной, есть два смежных ребра, которые встречаются там.Поскольку по крайней мере одно из этих двух ребер ограничивает пятиугольник, по условию (3) нет вершины, в которой встречаются только шестиугольники. Таким образом, в каждой вершине есть пятиугольник. Его стороны встречаются с шестиугольниками, а стороны шестиугольников попеременно встречаются с пятиугольниками и шестиугольниками. Это условие может быть выполнено, только если грани расположены вокруг вершины в последовательности черный, белый, белый, черный, белый, белый и т. Д. (Помните, что пятиугольники черные.) вершине, количество граней, которые встречаются в этой вершине, должно быть кратно 3.Это означает, что локально вокруг любой вершины структура выглядит так же, как разветвленное покрытие стандартного футбольного мяча вокруг точки ветвления. Теория покрывающих пространств — часть топологии, изучающая отношения между пространствами, которые выглядят локально похожими, — затем позволила нам доказать, что любой футбольный мяч на самом деле является разветвленным покрытием стандартного покрытия.
Для математиков обобщение — вторая натура. Даже после того, как что-то было доказано, может быть неясно, почему именно это правда.Проверка аргумента в несколько разных ситуациях при исследовании обобщений — важная часть его реального понимания и определения того, какие из используемых допущений являются существенными, а от каких можно отказаться.
Беглый взгляд на приведенные выше аргументы показывает, что в анализе футбольных мячей очень мало зависит от того, что они состоят из пятиугольников и шестиугольников. Поэтому естественно определить «обобщенные футбольные мячи», допускающие использование других видов многоугольников.Представляя, что мы снова раскрашиваем грани в черный и белый, мы предполагаем, что черные грани имеют х краев, а белые грани имеют х краев каждая. Для обычных футбольных мячей k равно 5, а l равно 6. Как и раньше, края черных граней должны соответствовать только кромкам белых граней, а кромки белых граней попеременно встречаются с кромками черного и белого. лица. Чередование цветов заставляет l быть четным числом.
Сделав еще один шаг в этом процессе обобщения, мы можем потребовать, чтобы каждое n -е ребро белой грани совпадало с черной гранью, а все остальные его грани встречались с белыми гранями. Это заставляет l быть кратным n ; то есть l = m ´ n для некоторого целого числа m . Конечно, мы по-прежнему требуем, чтобы края черных граней соответствовали только белым граням. Назовем такой многогранник обобщенным футбольным мячом .Таким образом, шаблон обобщенного футбольного мяча описывается тремя целыми числами (k, m, n), , где k — количество сторон на черной лицевой стороне, l = m ´ n — количество сторон белой грани, и каждые n -ая сторона белой грани встречается с черной гранью. Первый вопрос, который мы должны задать: какие комбинации k, m и n на самом деле возможны для обобщенного футбольного мяча? Оказывается, ответ на этот вопрос тесно связан с правильными многогранниками.
Древнегреческие математики и философы были очарованы правильными многогранниками, также известными как Платоновы тела , что приписывало им множество мистических свойств. Платоновы тела — это многогранники с максимально возможной степенью симметрии: все их грани представляют собой равносторонние многоугольники с одинаковым количеством сторон, и одинаковое количество граней пересекается в каждой вершине. Евклид доказал в своей работе Elements , что таких многогранников всего пять: тетраэдр, куб, октаэдр, додекаэдр и икосаэдр (см. Рис. 7 ).
Хотя Евклид использовал геометрическое определение Платоновых тел, предполагая, что все многоугольники правильные, современные математики знают, что этот аргумент не зависит от геометрии. Фактически, топологический аргумент с использованием только формулы Эйлера показывает, что не существует других возможностей, кроме пяти, показанных на рисунке 7.
Каждое платоново тело можно описать двумя числами: числом K вершин на каждой грани и числом M граней, пересекающихся в каждой вершине.Если f — количество граней, то общее количество ребер составляет e = (1/2) K ´ f , а количество вершин составляет v = (1 / M) K ´ . f . Подставляя эти значения в формулу Эйлера f — v + e = 2, мы обнаруживаем, что элементарная алгебра приводит к уравнению:
Возможные решения могут быть определены довольно легко. Полный список возможных значений для пар (K, M) :
(3, 3) для тетраэдра
(4, 3) и (3, 4) для куба и октаэдра
( 5, 3) и (3, 5) для додекаэдра и икосаэдра.
Строго говоря, это только список подлинных многогранников, удовлетворяющих приведенному выше уравнению. У уравнения есть и другие решения в положительных целых числах. Эти решения соответствуют так называемым вырожденным платоновым телам s, которые не являются истинными многогранниками. Одно семейство этих вырожденных многогранников имеет произвольные K = 2 и M , а другое — M = 2 и K произвольно. Первый случай можно представить себе как пляжный мяч, который представляет собой сферу, разделенную на части M , как цитрусовые.
Платоновы тела создают обобщенные футбольные мячи с помощью процедуры, известной как усечение . Предположим, мы берем острый нож и отрезаем каждый из углов икосаэдра. В каждой из 12 вершин икосаэдра пять граней сходятся в одной точке. Когда мы отрезаем каждую вершину, мы получаем небольшой пятиугольник, одна сторона которого граничит с каждой из граней, которые раньше встречались в этой вершине. При этом мы меняем форму 20 треугольников, составляющих грани икосаэдра.Срезая углы треугольников, превращаем их в шестиугольники. Стороны шестиугольников бывают двух видов, которые встречаются попеременно: остатки сторон исходных треугольных граней икосаэдра и новые стороны, полученные путем отсечения углов. Первая сторона граничит с другим шестиугольником, а вторая — с пятиугольником. По сути, полученный многогранник — не что иное, как стандартный футбольный мяч. Математики называют это усеченным икосаэдром .
Та же процедура усечения может быть применена к другим Платоновым телам. Например, усеченный тетраэдр состоит из треугольников и шестиугольников, так что стороны треугольников пересекаются только с шестиугольниками, а стороны шестиугольников попеременно встречаются с треугольниками и шестиугольниками. Это обобщенный футбольный мяч с k = 3, m = 3, n = 2 (и l = m ´ n = 6). Усеченный икосаэдр дает значения для k, m и n из 5, 3 и 2.Остальные усечения дают (k, m, n) = (4, 3, 2) для октаэдра, (3, 4, 2) для куба и (3, 5, 2) для додекаэдра. Кроме того, мы можем усечь пляжные мячи, чтобы получить обобщенные футбольные мячи с (k, m, n) = (k , 2, 2), где k может быть любым целым числом больше 2.
Это единственные возможности для обобщенных моделей футбольных мячей, или есть другие? Опять же, мы можем ответить на этот вопрос, используя формулу Эйлера: f — e + v = 2.Так же, как мы сделали для Платоновых тел, мы можем выразить количество граней, ребер и вершин в терминах наших основных данных. Вот это число b черных граней, число w белых граней и параметры k , m и n . Теперь, поскольку количество граней, пересекающихся в вершине, не фиксировано, мы получаем не уравнение, а неравенство, выражающее тот факт, что количество граней, пересекающихся в каждой вершине, не меньше 3.Результатом является ограничение на k, m и n , которое можно представить в следующей форме: :
Это может показаться сложным, но его легко проанализировать, как и уравнение, приводящее к платоновым телам. Нетрудно показать, что n может быть не более 6, потому что в противном случае левая часть была бы больше правой. Приложив немного больше усилий, можно составить полный список всех возможных решений в целых числах k, m и n .
Увы, на этом история не заканчивается. Есть несколько троек, например (k, m, n) = (4, 4, 1), которые удовлетворяют неравенству для подходящих значений b , но не возникают из обобщенных футбольных мячей. Однако Браунгардт и я смогли определить значения (k, m, n) , которые действительно реализованы как футбольные мячи; они показаны в таблице на рисунке 9, где мы также проиллюстрировали самые маленькие реализации для нескольких типов. Обратите внимание, что все с n = 2 происходят от усечений Платоновых тел.
Перечисленные здесь многогранники обладают различными интересными свойствами, из которых я упомяну только одно. Помимо записи 10 в этой таблице, которая, конечно, является стандартным футбольным мячом, таблица содержит еще три фуллерена: числа 14 и 20 и случай k = 6 записи 17. Число шестиугольников в этих примерах равно 30, 60 и 2 соответственно. (Обратите внимание, что в последнем случае цветовая схема меняется на обратную, поэтому шестиугольники черные, а не белые.) Число атомов углерода составляет 80, 140 и 24 соответственно.Последний из них — единственный фуллерен с 24 атомами. В случае 80 атомов имеется 7 различных фуллеренов с непересекающимися пятиугольниками, но только один встречается в нашей таблице обобщенных футбольных мячей. На 140 атомов приходится 121 354 фуллерена с непересекающимися пятиугольниками.
Браунгардт и я обнаружили кое-что очень интригующее, когда попытались выяснить, происходит ли каждый обобщенный футбольный мяч из разветвленного покрытия одной из записей в нашей таблице. Это верно, как мы обнаружили, для всех троек с n = 2, то есть для обобщенных футбольных мячей, у которых черные и белые грани чередуются по сторонам каждой белой грани.Однако это неверно для других значений n ! Самый простой пример, демонстрирующий эту неудачу, возникает для тройки (k, m, n) = (3, 1, 3), что означает, что у нас есть черные и белые треугольники, расположенные таким образом, что стороны каждого черного треугольника пересекаются только белые, и у каждого белого треугольника ровно одна сторона пересекается с черной. Минимальный пример — это просто тетраэдр с одной гранью, окрашенной в черный цвет (рис. 10а). Другая реализация — октаэдр с двумя противоположными гранями, окрашенный в черный цвет (Рис. 10b) .Это не разветвленное покрытие нарисованного тетраэдра! Разветвленное покрытие тетраэдра будет иметь 3, 6, 9,… граней, пересекающихся в каждой вершине, но у октаэдра их 4.
Причина такого странного поведения — тонкая разница между случаем n = 2 и случаями n > 2. В примере с тетраэдром есть два разных типа вершин: вершина, в которой встречаются только белые грани, и три вершины, где встречаются одна черная и две белые грани.Кроме того, у раскрашенного октаэдра есть еще одна вершина. Но в случае n = 2 все вершины выглядят практически одинаково. Каждая вершина имеет одну и ту же последовательность цветов: черный, белый, белый, черный, белый, белый,…, с открытой только длиной последовательности. Таким образом, условия смежности обеспечивают степень контроля над локальной структурой любого обобщенного футбольного мяча с n = 2. Этот элемент управления отсутствует в случае n > 2.Таким образом, в настоящее время можно описать все обобщенные футбольные мячи с n = 2: они представляют собой разветвленные покрытия усеченных Платоновых тел. Но нет простого способа получить все обобщенные футбольные мячи с n > 2.
С точки зрения тополога сферические футбольные мячи — лишь один из примеров карт, нанесенных на поверхности. Поскольку определение футбольных мячей с помощью условий (1), (2) и (3) не указывает, что многогранники футбольных мячей должны быть сферическими, существует вероятность того, что они могут существовать и в других формах.Помимо сферы, может возникнуть бесконечно много других поверхностей: тор (который является поверхностью бублика), двойной тор, тройной тор (который является поверхностью кренделя), четверной тор и т. Д. Поверхности отличаются друг от друга своим родом , неофициально известным как количество отверстий: сфера имеет род ноль, тор имеет род один, двойной тор имеет род два и т. д.
Существуют футбольные мячи всех родов, потому что каждая поверхность представляет собой разветвленное покрытие сферы (в несколько более общем смысле, чем мы обсуждали ранее).Расположив точки ветвления как вершины графа футбольных мячей на сфере, мы можем создать графы футбольных мячей на любой поверхности. На рис. 11а показан футбольный мяч тороидальной формы, полученный из двояко разветвленного покрытия стандартного сферического мяча. В этом случае есть четыре точки ветвления. Обратите внимание, что двунаправленное разветвленное покрытие всегда удваивает количество пятиугольников и шестиугольников.
Вот более простая конструкция тороидального футбольного мяча. Возьмите стандартный сферический футбольный мяч и разрежьте его по двум непересекающимся краям.Открытие сферы вдоль каждого разреза дает нечто похожее на сферу, из которой были удалены два диска. На этой поверхности изображен футбольный мяч, а у двух граничных окружностей, на которых мы открыли сферу, есть две вершины. Если обрезанные края имеют один и тот же тип, что означает, что по обеим сторонам две белые грани встретились в исходном сферическом футбольном мяче, или что на обоих из них черная грань встретилась с белой гранью, то мы можем склеить два граничных круга вместе. так, чтобы вершины совпадали с вершинами.(См. Рисунок 11b для пошаговых иллюстраций этой конструкции.) Построенная таким образом поверхность снова является тором. Он имеет структуру многогранника, удовлетворяющего условиям (1), (2) и (3), и поэтому является футбольным мячом.
Этот второй тороидальный футбольный мяч не является разветвленным покрытием стандартного сферического мяча, потому что он имеет такое же количество пятиугольников и шестиугольников (12 и 20 соответственно), что и стандартный сферический мяч. Для разветвленного покрытия эти числа умножаются на степень покрытия.В этом случае отказ вызван не потерей контроля над локальной структурой паттерна (как в предыдущем разделе), а глобальным свойством тора (дыра). Таким образом, основной результат, что все сферические футбольные мячи представляют собой разветвленные покрытия стандартного, неверен для футбольных мячей с отверстиями.
Футбольные мячи наглядно демонстрируют тесную связь, существующую между графами на поверхностях и разветвленными покрытиями. Этот круг идей также связан с тонкими вопросами алгебраической геометрии, где комбинаторика карт на поверхностях таинственным образом инкапсулирует данные теории чисел.Следуя терминологии, введенной Александром Гротендиком, одним из ведущих математиков 20 века, соответствующие графы на сфере в настоящее время называются dessins d’enfants .
- Braungardt, V., and D. Kotschick. 2006. Классификация футбольных паттернов. Препринт. http://129.187.111.185/~dieter/football.pdf
- Brinkmann, G., and A. W. M. Dress. 1997. Конструктивное перечисление фуллеренов. Журнал алгоритмов 23: 345-358.
- Bundeswettbewerb Mathematik. 1988. Aufgaben und Lösungen , 1983–1987 годы. Штутгарт, Германия: Эрнст Клетт Верлаг.
- Chung, F., and S. Sternberg. 1993. Математика и бакибол. Американский ученый 81: 56-71.
- Кокстер, Х. С. М. 1948. Правильные многогранники . Лондон: Methuen & Co. Ltd.
- Schneps, L. (ed.). 1994. Теория Гротендика о детской одежде. Серия лекций Лондонского математического общества, т. 200. Кембридж, Великобритания: Издательство Кембриджского университета.
- Якобсон Б. И. и Р. Э. Смолли. 1997. Фуллереновые нанотрубки: C 1,000,000 и выше. Американский ученый 85: 324-337.
Обратная полная замена плеча | Хирургия плеча и локтя Johns Hopkins
Основное различие между стандартной заменой плеча и обратной процедурой заключается в том, что при обратной замене плеча шаровые и впадинные части плечевого сустава меняют стороны.Это означает, что их естественное положение перевернуто. Обратная полная замена плеча — сложная процедура, требующая определенных условий. Позвоните, чтобы записаться на прием к одному из наших специалистов по плечу, если у вас есть проблемы с плечом, которые могут потребовать замены плеча.
Почему эти замены плеча называют «обратным» протезом?
Протезы плечевого сустава предназначены для удаления частей костей плечевого сустава, пораженных артритом (отсутствующий хрящ).Плечевой сустав представляет собой шаровидный сустав с шаровой опорой (или головкой плечевой кости), которая является частью плечевой кости, и плоской поверхностью (которая называется впадиной), которая является частью лопатки (рис. 1). При стандартной замене плечевого сустава шарообразная часть плеча (головка плечевой кости) заменяется металлическим шариком, а гнездо заменяется пластиковой деталью (Рисунок 2).
В «обратном протезе» плечевой сустав по-прежнему заменяется деталями или компонентами из металла и пластика (рис. 3).Большая разница между реверсивным протезом и стандартным протезом плеча заключается в том, что в реверсивном протезе мяч размещается на стороне сустава со стороны гнезда. Это противоположно тому, где он находится в природе, или «противоположно» тому, что вы ожидаете. Затем гнездо помещается на стороне руки, где оно поддерживается металлическим стержнем в кости руки (плечевой кости) (рис. 4). Таким образом, мяч и гнездо полностью противоположны тому, что происходит в природе.
Как они держатся вместе?
К счастью, обратный протез можно установить с помощью винтов на стороне гнезда, которые удерживают его в кости лопатки (рис. 3 и 4).Затем шарик ввинчивается в пластину, которая была прикреплена к гнезду (Рисунок 3).
Часть протеза, помещенная в кость руки, фиксируется цементом, который связывает металл с костью в течение нескольких минут (рис. 4). Затем пластмассовый патрубок запрессовывается в конец штока, где он надежно фиксируется путем фиксации в металлической детали. Это позволяет гнезду вращаться на шаре, так что движение плеча может быть восстановлено (Рисунок 5). Мышцы плеча также помогают удерживать обратный протез на месте.
Почему человеку следует делать обратный протез вместо стандартного протезирования плеча?
Стандартная полная замена плеча зависит от целостности мышц и сухожилий плечевого сустава. Мышцы прикрепляются к лопатке и превращаются в сухожилия, прикрепляющиеся к плечу. Эти мышцы и их сухожилия служат для движения плеча и вместе называются вращающей манжетой. Когда эти сухожилия сильно разрываются, так что они больше не прикрепляются к кости, плечо часто не функционирует нормально.Потеря вращающей манжеты может вызвать боль и потерю подвижности. Обычная замена плеча работает только в том случае, если эти сухожилия не повреждены. Напротив, обратный протез предназначен для ситуаций, когда вращающая манжета порвана или неисправна.
Воспроизвести видео:Какие состояния плечевого сустава требуют полной обратной замены плечевого сустава?
Основной причиной выбора обратного протеза является артрит плечевого сустава и разрыв или отсутствие сухожилий вращательной манжеты плеча.Это наиболее частое хирургическое показание для пациента, желающего установить обратный протез. В этой ситуации эта операция принесет пациенту значительное облегчение боли, а также может помочь с диапазоном движений плеча. Хотя диапазон движений после обратного протеза может быть не полностью нормальным, он обычно улучшается по сравнению с движением, ранее утраченным из-за артрита и боли.
Другой причиной использования обратного протеза является разрыв всех сухожилий вращательной манжеты плеча и невозможность поднять руку достаточно высоко для функционирования.Обычно в этом случае плечо не вызывает боли, но невозможность поднять руку очень мешает жизнедеятельности. Когда пациент поднимает руку, на передней части плеча появляется выступ, и это называется передне-верхней миграцией или подвывихом плеча. В этих случаях боль может быть или не быть основным фактором для обратного протеза, но основной причиной замены является восстановление движения и функции.
Третьей наиболее частой причиной использования обратного протеза является то, что плечо уже было заменено до того момента, когда обратный протез был доступен, и у пациента все еще сохраняется боль и потеря движения.Иногда при переломе или разрыве сухожилий вращательной манжеты плеча выполнялась обычная замена плеча, и плечо продолжало болеть. В этом случае, если требуется обратный протез, операция по установке обратного протеза немного сложнее. Причина этого в том, что первая, более традиционная замена плеча должна быть удалена во время операции, а обратная сторона может быть помещена в плечо.
Другими причинами использования обратного протеза являются некоторые переломы плечевой области, особенно те, которые затрагивают проксимальный отдел плечевой кости (кость руки), где мяч прикрепляется к стержню кости.В некоторых случаях кость разбивается на множество частей или мяч может быть разделен на части.
Последней причиной использования обратного протеза является опухоль в проксимальном отделе плечевой кости, которая затрагивает кость диафиза кости или сам шар плечевой кости.
Как выглядит операция?
Операция очень похожа на обычную замену плеча с некоторыми вариациями. Основным фактором выздоровления является то, будет ли это первая замена плеча или старый протез придется снимать во время операции.Когда это делается, это называется «ревизионным» случаем, и восстановление может отличаться от того, когда выполняется первая (так называемая «первичная») замена сустава.
Операция обычно проводится с блокадой нерва руки с последующей общей анестезией. Разрез находится в передней части плеча, и операция занимает от двух до трех часов. Послеоперационное обезболивание достигается с помощью обезболивающих перорально и, при необходимости, через вену. Большинство пациентов могут начать двигать пальцами, запястьями и локтями на следующий день.
Начнется ли движение плеча на следующий день после операции, зависит от того, насколько хорошо опорная пластина и шарик прикреплены к гнезду винтами. В обратном протезе есть некоторая зависимость от заживления кости вокруг базовой пластины и винтов. В результате движение плеча может быть остановлено от нескольких дней до нескольких недель. Несмотря на эти меры предосторожности, большинству пациентов разрешается есть, читать или пользоваться клавиатурой конечностями в течение нескольких дней после операции. Величина, на которую пациент может поднять руку, зависит от многих факторов, и каждый пациент индивидуален.Количество движений, разрешенных пациенту после операции, также зависит от фиксации винтов к кости, что может быть определено во время операции. Наконец, количество движений, восстановленных после этой операции, также зависит от того, сколько движений было у пациента до операции.
Большинство пациентов сдают перед операцией единицу крови, которую при необходимости можно вернуть. При первой замене сустава кровь возвращается пациенту обычно только в 10-20% случаев.В ревизионных случаях, когда операция длится дольше, почти в 80% случаев требуется переливание крови. Точно так же продолжительность операции больше для повторных случаев (от трех до пяти часов), а время восстановления для восстановления функции руки больше. Другие факторы, влияющие на время восстановления, включают в себя то, проведена ли костная пластика (добавление кости там, где она отсутствует), хорошо ли она держится и сколько времени требуется кость для заживления.
Каких результатов я могу ожидать от полной обратной замены плеча?
Обратный протез очень хорошо обезболивает.Исследования, проведенные в Европе, показывают, что примерно 85-90% пациентов, перенесших эту процедуру, получают отличное обезболивание. Степень обезболивания во многом зависит от причины, по которой была проведена процедура. Степень обезболивания при повторных операциях немного ниже, чем при процедурах, проводимых впервые, и считается, что это связано с образованием рубцов и долгосрочными повреждениями.
Обратный протез также должен восстановить некоторый диапазон движений плеча, но степень возврата не так предсказуема, как обезболивание.Большинство пациентов получают возможность дотянуться до макушки без необходимости наклонять голову. Большинство пациентов видят улучшение движения в других направлениях, но если их вращательная манжета полностью разорвана, они могут не увидеть улучшения в способности дотягиваться в сторону от тела (так называемое «внешнее вращение»).
Долгосрочная выживаемость обратного протеза (то есть, как долго оно может оставаться в плече, прежде чем начнется расшатывание и потребуется дополнительная операция) обратного протеза была благоприятной.Обратный протез используется во Франции с 1980-х годов, но был одобрен Управлением по санитарному надзору за качеством пищевых продуктов и медикаментов (FDA) в США в апреле 2004 года. В результате в настоящее время в США нет долгосрочных исследований его использования. . Однако опыт плечевых хирургов и пациентов из Европы, кажется, указывает на то, что протез прослужит 15 лет примерно в 90% случаев.
Каковы возможные осложнения этой процедуры?
Осложнения этой процедуры аналогичны осложнениям при замене любого сустава тела.Есть осложнения, аналогичные осложнениям при обычной замене плеча, и пара уникальных для этого протеза.
Наиболее частым осложнением является то, что плечевая кость или часть руки (впадина) могут оторваться от мяча (часть лопатки) и протез «смещен». В основном две части протеза больше не связаны. Это осложнение чаще встречается при обратном протезировании, чем при обычной замене плеча. К счастью, с этим обычно можно справиться, поместив руку обратно в нужное место и обездвиживая ее на некоторое время.Если протез продолжает смещаться, иногда требуется дополнительная операция, чтобы исправить положение.
Вторым по частоте осложнением после обратного протеза является инфекция. Это происходит редко, но если это происходит, то это может расстроить как пациента, так и врача. Иногда инфекцию можно контролировать с помощью хирургического вмешательства по промыванию сустава и антибиотиков. Если инфекция становится хронической, несмотря на лечение, существуют варианты решения проблемы, но в большинстве случаев они включают в себя дальнейшее хирургическое вмешательство.
Еще одним осложнением этого протеза является то, что часть руки может контактировать с костью лопатки в определенных положениях. Этот контакт может создать бороздку в кости лопатки, которая обычно безболезненна. Обычно это осложнение не требует дальнейшего хирургического вмешательства и поддается лечению, избегая положения рук и с помощью лекарств.
Другие осложнения очень редки, но редко наблюдаются при использовании этого протеза или при регулярной замене плечевого сустава.К ним относятся покалывание, онемение и слабость, если нервы руки растянуты во время операции. Повреждение кровеносных сосудов случается очень, очень редко, но может произойти, особенно когда очень сильно пугает и пациент перенес несколько операций. Проблемы со здоровьем, такие как сгустки крови в ногах (тромбоз глубоких вен), которые могут попасть в легкие (тромбоэмболия легочной артерии), сердечные приступы, инсульты, лекарственные или анестезирующие реакции могут возникнуть при любой операции, но, по нашему опыту, они очень опасны. редко после операции по замене плеча.
Кому нельзя делать обратный протез?
Есть всего несколько случаев, когда обратный протез не может быть имплантирован. Во-первых, если лунка (лопатки или лопатки) заходит слишком далеко, чтобы можно было прикрепить пластину основания компонента винтами к кости. В некоторых случаях костный трансплантат может быть добавлен во время операции, что позволяет разместить опорную пластину и винты, или может быть добавлен костный трансплантат, чтобы позволить разместить опорную пластину позже.
Пациенты с продолжающейся инфекцией плеча не должны иметь обратный протез. Однако, если инфекцию удастся устранить, можно будет вставить протез. Когда бы ни пытались заменить плечо в плече, которое ранее было инфицировано, уровень послеоперационной инфекции выше, чем если бы в плече никогда не было инфекции. Это следует подробно обсудить с врачом перед операцией.
Ссылки
Frankle M, Siegal S, Pupello D, Saleem A, Mighell M, Vasey M.Обратный протез плеча при артрите плечевого сустава, связанном с тяжелым дефицитом вращающей манжеты плеча. Минимальное двухлетнее наблюдение с участием шестидесяти пациентов. J Bone Joint Surg Am 2005; 87 (8): 1697-705
Grammont PM, Baulot E. Протез плечевого сустава в форме дельты при разрыве вращательной манжеты. Ортопедия 1993; 16 (1): 65-8.
Valenti P, Boutens D, Nerot Cea. Обратный протез Delta 3 при остеоартрозе с массивным разрывом вращательной манжеты плеча: долгосрочные результаты. В: Walch G, Boileau P, Mole D, редакторы.2000 Протез плеча. от двух до десяти лет наблюдения. Монпелье: Sauramps Medical; 2001. с. 253-259.
Werner CM, Steinmann PA, Gilbart M, Gerber C. Лечение болезненного псевдопареза из-за непоправимой дисфункции вращательной манжеты плечевого сустава с помощью тотального плечевого протеза Delta III с шарнирно-шарнирной головкой. J Bone Joint Surg Am 2005; 87 (7): 1476-86.
Boulahia A, Edwards TB, Walch G, Baratta RV. Первые результаты протеза обратной конструкции при лечении артрита плеча у пожилых пациентов с большим разрывом вращательной манжеты плеча.Ортопедия 2002; 25 (2): 129-33.
Риттмайстер М., Кершбаумер Ф. Обратное тотальное эндопротезирование плеча по Граммонту у пациентов с ревматоидным артритом и невосстановимыми поражениями вращающей манжеты плеча. J. Хирургия плечевого и локтевого суставов 2001; 10 (1): 17-22.
Sirveaux F, Favard L, Oudet D, Huquet D, Walch G, Mole D. Тотальное эндопротезирование плечевого сустава методом Граммона при лечении плечевого остеоартроза с массивным разрывом манжеты. Результаты многоцентрового исследования 80 плеч.J Bone Joint Surg Br 2004; 86 (3): 388-95.
Hatzidakis AM, Norris TR, Boileau P. Обратное эндопротезирование плеча; Показания, методика и результаты. Методы хирургии плеча и локтя 2005; 6 (3): 135-154.
Защита длинных мячей — Soccer Coach Weekly
При защите длинных мячей важно, чтобы один игрок атаковал мяч, в то время как другие защитники отставали, чтобы прикрыть его и оказать поддержку. Это занятие улучшит понимание ваших защитников в таких ситуациях.
О чем эта сессия
- Защита длинных мячей.
- Получение высоты и расстояния на ваших зазорах.
- Хорошая защитная форма и укрытие.
Что думать о
Когда длинный мяч направлен в вашу защиту, важно, чтобы один из ваших защитников атаковал мяч и не позволял ему отскакивать от вашей штрафной площади. Также важно, чтобы заголовок был очищен от высоты и расстояния.
Остальные защитники всегда должны предвидеть, что атакующий соперник может выиграть удар головой и подбросить мяч к воротам. Следовательно, другие ваши защитники должны отойти за защитником, атакующим мяч, чтобы обеспечить прикрытие и поддержку.
Установка
- Создайте зону размером 50 на 30 ярдов с четырьмя манекенами / шестами, расположенными вдоль средней линии.
- Для игры удалите манекены / шесты и поставьте ворота на обоих концах с двумя вратари.
| Разминка | Сессия | Разработки | Игровая ситуация | Разминка |
|---|---|---|---|---|
| 10 минут | 15 минут | 15 минут | 10 минут | 10 минут |
Что вы заставляете своих игроков делать
Защитники пронумерованы от 1 до 4. Вы называете определенный номер. Подающий перебрасывает мяч через манекены, и пронумерованный защитник должен отреагировать, чтобы атаковать мяч в воздухе.
Целью защитника является попадание мяча головой в зачетную зону соперника, чтобы набрать очко за набор высоты и дистанции при их выносе.
Вы называете номер, и подающий быстро бросает мяч этому защитнику, чтобы он смог пройти мимо.
Развитие
Теперь соперники перебрасывают мяч вдоль своей линии. Защитники должны занять защитную форму и позицию по отношению к мячу. Противники могут случайным образом бросить высокий мяч над манекенами, чтобы защитник мог их очистить.
На этот раз команда получает одно очко за эффективный проход в зачетную зону и дополнительное очко за прикрытие позиций остальных трех защитников.
Серая команда случайным образом забрасывает высокий мяч в половину поля соперника. Ближайший защитник бьет головой, а другие защитники прикрывают его.
Игровая ситуация
Серая команда выстраивается в линию с вратарём, четырьмя защитниками и тремя полузащитниками против вратаря белой команды, тремя полузащитниками и двумя нападающими.У белой команды есть два подающих, которым они могут передать пас.
Для начала, четверка защитников серой команды должна находиться на своей линии защиты и получать длинный мяч от подающего.
Играть в обычный футбол и возобновить игру длинным мячом, если забит гол или мяч выходит из игры.
Сервер начинает игру длинным мячом. Могут ли защитники отбивать мяч и наращивать обороты?
Куда звонить
- «Реагировать и атаковать мяч»
- «Высота и расстояние на просвет»
- «Оставь своего товарища по команде, чтобы укрыться»
О Тони Карре
Тони Карр — одна из самых влиятельных фигур в английском футболе.Бывший директор Академии Вест Хэма вывел из молодежной команды в первую команду таких игроков, как Глен Джонсон, Джон Терри, Рио Фердинанд, Фрэнк Лэмпард, Майкл Каррик, Джо Коул и Джермейн Дефо.
Behind Bears QB Nick Foles «уникальный глубокий мяч»
Если глубокий мяч Митча Трубиски — это подача Рики Вона — «Дикая Вещь» никогда не знала, куда летит мяч, хотя и добралась туда быстро, то удар Ника Фоулза клином по дуге, предназначенный для того, чтобы влететь в руки его приемники.
«Я думаю, это больше похоже на ощущение, просто понимание скорости и угла наклона приемников, а также того, где они будут находиться», — сказал на этой неделе Фоулс, новый стартовый квотербек «Медведей». «И просто позволяя ему разорваться».
Фоулс сделал это — потому что он был вынужден — в камбэке Bears в четвертой четверти с 16 очками, выигравшем у Falcons. Он будет более рассудительным в том, как часто он будет проводить глубокие воскресенья против Кольтов на Солдат-Филд, но нет сомнений, что он даст Медведям новое оружие.
Фоулс сочетает в себе силу рук, способность оценивать скорость приемников и угол их маршрутов, а также размер (он стоит 6-6), чтобы видеть поле.
Тогда вот отношение.
«У Ника всегда был агрессивный склад ума», — сказал тренер Мэтт Надь. «Это никогда не менялось. Нам это понравилось. . . . Когда у вас есть такая точность на этих глубоких мячах, это всегда положительно для нападения — и для этих широких приемных и узких концов «.
Надь всегда приравнивал передачу касанием к броску в баскетбол — и сразу же отмечает мастерство Фолза в обручах.Фоулс обладает «уникальным глубоким мячом», — сказал три года назад тренер Кольтс Фрэнк Райх, его координатор по команде Eagles, выигравшей Суперкубок.
«Многие ребята, которые сегодня бросают глубокий мяч, придают мячу более плоский вид», — сказал Райх. «Ник бросает мяч по большой дуге».
Это дает принимающим шанс опередить защитников по мячу, будь то Алшон Джеффри в Филадельфии или Аллен Робинсон в этом сезоне.
Фоулс никогда не бросал глубже, чем во время Суперкубка.По данным Pro Football Focus, с 15 недели до второго раунда плей-офф он забросил одно завершение и один перехват при 13 передачах на 20 ярдов и более. В титульном матче NFC и Суперкубке вместе взятых, он пошел 8 из 12 на 274 ярда, четыре тачдауна и один перехват при таких бросках.
«Если вы доверяете своим парням, они могут сыграть роль», — сказал Райх. «Вот что говорит [Фоулс] — он просто предполагает, что они собираются сыграть больше розыгрышей, чем нет. И в этом он добился больших успехов в своей карьере.”
У Медведей нет. В прошлом году Трубский выполнил 45,7% из своих 46 передач на 20 ярдов и более — оба показателя заняли 17-е место в лиге. Ресиверам приходилось прикусить язык, особенно в середине сезона, когда их расстраивали броски Трубского.
Ранее на этой неделе тренера приемных Майка Фурри спросили о бросках через плечо, когда квотербек видит, как принимающий и угловой защитник бегут наравне друг с другом, и решает бросить мяч в заднее плечо принимающего.Фоулс попробовал один такой бросок на Джавона Вимса в четвертой четверти в прошлое воскресенье. Он не завершился, но Ферри сказал, что это долгожданное изменение.
«Очевидно, что за последние два-три года у нас не было много таких продуктов», — сказал Фурри. «Так что это должно произойти сейчас».
Вимс был взволнован, увидев даже такую попытку.
«Я думаю, что одна из величайших вещей — это когда Ник бросил его, а [Вимс] сошел с боковой линии», — сказал Фурри. «[Вимс] сказал:« Эй, это снова как дни в колледже.Если я не открою, то обратное плечо.
«Это происходит, потому что мы бросаем мяч по полю».
Это плохой знак, когда глубокая пасовая атака Трубинского не идет ни в какое сравнение с атакой Джорджии Бульдогс.
Фигурки Фолса будут разными.
«Я думаю, что на протяжении всей своей жизни я часто бросаю мяч, это очень важно», — сказал Фоулс. «В этом нет ничего особенного. Это чувство — просто отпустить мяч и просто повеселиться.”
Задача одномерной кинематики: мяч, брошенный прямо вверх — Физика
Шаг 1:
Скорость, когда мяч покинул вашу руку (точка 1) — это информация, запрошенная в части а) задачи.
————————————————- ——————————————-
Шаг 2:
В части b) задачи запрашивалось количество времени, в течение которого мяч находился в воздухе (между точками 1 и 3.) Никаких дополнительных математических решений не требуется.
В постановке задачи указаны все вертикальные положения относительно земли, поэтому я выбрал землю в качестве точки y = 0.
Первый момент, описанный в задаче, — это когда мяч покидает вашу руку. В этой точке мяч находится на высоте 1,2 м над землей, которая была выбрана в качестве контрольной точки y = 0. Вы не знаете, с какой скоростью движется мяч, когда он покидает вашу руку, поэтому v 1 неизвестно.
Мяч поднимается на высоту 3.3 м над землей или 3,3 м над точкой y = 0. На этом этапе у вас также есть информация о скорости. Вы знаете, что гравитация заставляет объект замедляться при движении вверх и ускоряться при движении вниз. В верхней части движения (наивысшая точка) вертикальная (или y) составляющая скорости объекта равна нулю.
В последней точке задачи мяч достигает земли или нулевой высоты. Очень распространенная ошибка полагать, что скорость мяча в этой точке равна нулю.Но помните, что кинематические уравнения применимы только в периоды постоянного ускорения. Как только мяч касается земли, земля очень быстро замедляет его — у него больше нет ускорения, равного g. Итак, точка 3 — это точка непосредственно перед тем, как мяч коснется земли.
В этом случае мяч движется строго вертикально. У вас есть только движение в направлении y. Следовательно, вам не нужно разделять какие-либо переменные на их x- и y-компоненты.
Я нарисовал движение мяча по параболе, а не прямо вверх и вниз, только для того, чтобы четко обозначить точки 1, 2 и 3 на рисунке.
t в кинематических уравнениях относится к интервалу времени между двумя точками в уравнении, причем y 0 встречается в более ранний момент времени. Я использую Δt вместо t, чтобы явно указать, что это временной интервал (t — t 0 ), а не момент времени.
В некоторых учебниках приводится более трех кинематических уравнений — например, они могут содержать «уравнения дальности» или различные версии уравнений для горизонтального и вертикального движения. Это как раз те три уравнения, которые решаются для частных случаев.На мой взгляд, лучше знать и понимать три уравнения, которые всегда будут работать, чем запоминать множество уравнений, характерных только для определенных ситуаций.
Вам предлагается найти скорость мяча в точке 1 (когда он покидает вашу руку), чтобы он имел необходимое движение в точке 2 (достигает высоты 3,3 м). Следовательно, «y 0 » и «y» — это «y 1 » и «y 2 » соответственно.
Ускорение мяча (из-за силы тяжести) направлено вниз, что является отрицательным y-направлением, выбранным в этой задаче.Поскольку a, v и y являются векторными величинами, их значениям должны быть присвоены знаки + или — для обозначения направления всякий раз, когда они вводятся в любое из кинематических уравнений.
Многие из наиболее распространенных ошибок в кинематических задачах можно избежать, внимательно следя за бухгалтерским учетом. Когда мы рисовали картинку, мы были осторожны, чтобы пометить каждую точку интереса другим нижним индексом, и когда мы заполняем уравнение, мы должны быть осторожны, чтобы ввести правильное значение для правильной точки.Мы не можем предположить, что нулевые значения совпадают с более ранним моментом времени. Фактически в этом выражении нулевая скорость возникает в верхней части движения (точка 2), а не в начале (точка 1).
В тексте задачи приведены только две значащие цифры, поэтому в решение включены только две значащие цифры.
Вас просят определить количество времени, которое требуется мячу, чтобы добраться от точки 1 (когда он покидает вашу руку) до земли (точка 3.) Следовательно, «y 0 » и «y» равны «y 1 » и «y 3 » соответственно.
Чтобы найти Δt в этом уравнении, примите во внимание, что у вас есть квадратное уравнение: оно имеет вид a Δt 2 + b Δt + c = 0, где a = -4,9, b = 6,4 и c = 1,2. (Быстрый взгляд на единицы показывает, что Δt должно быть в секундах, поэтому я не буду переносить единицы измерения в алгебру для решения квадратного уравнения просто потому, что я хочу избежать путаницы, когда вы сосредоточитесь на математике.)
Решение квадратного уравнения дается как:
Обратите внимание, что квадратная формула всегда дает два решения. По сути, это формула для полной параболической дуги, и двумя решениями будут времена, когда объект находится на любой заданной высоте в этой дуге (один раз поднимается, а один раз возвращается). В этом случае мяч не был брошен с земли. Если бы было брошено с земли (с такой скоростью, чтобы следовать по тому же пути), он получил бы 0.16 с, чтобы попасть с земли в руку. Чтобы вернуться от руки к земле, требуется еще 1,5 секунды, а это именно та информация, которую вы хотите найти.
Ускорение мяча (из-за силы тяжести) направлено вниз, что является отрицательным направлением оси y, выбранным в этой задаче. Поскольку a, v и y являются векторными величинами, их значениям должны быть присвоены знаки + или — для обозначения направления всякий раз, когда они вводятся в любое из кинематических уравнений.
В тексте задачи приведены только две значащие цифры, поэтому в решение включены только две значащие цифры.
Многие из наиболее распространенных ошибок в кинематических задачах можно избежать, внимательно следя за бухгалтерским учетом. Когда мы рисовали картинку, мы были осторожны, чтобы пометить каждую точку интереса другим нижним индексом, и когда мы заполняем уравнение, мы должны быть осторожны, чтобы ввести правильное значение для правильной точки. Мы не можем предположить, что нулевые значения совпадают с более ранним моментом времени. Фактически в этом выражении положение y = 0 происходит в конце движения (точка 3), а не в начале (точка 1.)
Обратите внимание, что квадратная формула всегда дает два решения. По сути, это формула для полной параболической дуги, и двумя решениями будут времена, когда объект находится на любой заданной высоте в этой дуге (один раз поднимается, а один раз возвращается). В этом случае мяч не был брошен с земли. Если бы он был брошен с земли (с такой скоростью, чтобы следовать по тому же пути), ему потребовалось бы 0,16 с, чтобы добраться от земли до вашей руки. Требуется дополнительный 1.5 секунд, чтобы вернуться из руки в землю, и это информация, которую вы хотите найти.
Как выбрать y = 0?
Все, что имеет значение для описания движения, — это то, что вы явно указываете, где находится ваша контрольная точка. В этом случае проблема давала высоту относительно земли, поэтому я выбрал точку отсчета. Если вы выбрали начальную точку (вашу руку) как y = 0, тогда земля будет на y = -1,2 м, а y 2 будет 2.1 мес. В любом случае вы получите одинаковые ответы.
Почему вы нарисовали траекторию мяча в виде параболы, а не показывали его прямо вверх и вниз?
Это просто для удобства отображения всех трех точек на диаграмме. Точка 3 действительно находится прямо под точкой 1.
В моей книге в уравнениях используется «t», а не «Δt». Это нормально?
илиМоя книга дает более трех уравнений. Почему вы используете только эти три?
t в кинематических уравнениях относится к интервалу времени между двумя точками в уравнении, причем y 0 встречается в более ранний момент времени.Я использую Δt вместо t, чтобы явно указать, что это временной интервал (t — t 0 ), а не момент времени.
В некоторых учебниках приводится более трех кинематических уравнений — например, они могут содержать «уравнения дальности» или различные версии уравнений для горизонтального и вертикального движения. Это как раз те три уравнения, которые решаются для частных случаев. На мой взгляд, лучше знать и понимать три уравнения, которые всегда будут работать, чем запоминать множество уравнений, характерных только для определенных ситуаций.
Как вы узнали, какие две точки выбрать?
Вас просят определить количество времени, которое требуется мячу, чтобы добраться от точки 1 (когда он покидает вашу руку) до земли (точка 3). Следовательно, «y 0 » и «y» равны «y». 1 »и« y 3 »соответственно.
Почему 9,8 м / с
2 отрицательно?Ускорение мяча (из-за силы тяжести) направлено вниз, что является отрицательным направлением оси y, выбранным в этой задаче.Поскольку a, v и y являются векторными величинами, их значениям должны быть присвоены знаки + или — для обозначения направления всякий раз, когда они вводятся в любое из кинематических уравнений.
Почему v
2 0 вместо v 1 ?Многие из наиболее распространенных ошибок в кинематических задачах можно избежать, внимательно следя за бухгалтерским учетом. Когда мы рисовали картинку, мы были осторожны, чтобы пометить каждую точку интереса другим нижним индексом, и когда мы заполняем уравнение, мы должны быть осторожны, чтобы ввести правильное значение для правильной точки.Мы не можем предположить, что нулевые значения совпадают с более ранним моментом времени. Фактически в этом выражении положение y = 0 происходит в конце движения (точка 3), а не в начале (точка 1).
Мои числа близки, но не совсем те, которые показаны в уравнении. Достаточно ли я близок?
В тексте задачи приведены только две значащие цифры, поэтому в решение включены только две значащие цифры.
Как вы узнали, какие две точки выбрать?
Вас просят определить количество времени, которое требуется мячу, чтобы добраться от точки 1 (когда он покидает вашу руку) до земли (точка 3.) Следовательно, «y 0 » и «y» равны «y 1 » и «y 3 » соответственно.
Почему 9,8 м / с
2 отрицательно?Ускорение мяча (из-за силы тяжести) направлено вниз, что является отрицательным направлением оси y, выбранным в этой задаче. Поскольку a, v и y являются векторными величинами, их значениям должны быть присвоены знаки + или — для обозначения направления всякий раз, когда они вводятся в любое из кинематических уравнений.
Почему v
3 0 вместо y 1 ?Многие из наиболее распространенных ошибок в кинематических задачах можно избежать, внимательно следя за бухгалтерским учетом.Когда мы рисовали картинку, мы были осторожны, чтобы пометить каждую точку интереса другим нижним индексом, и когда мы заполняем уравнение, мы должны быть осторожны, чтобы ввести правильное значение для правильной точки. Мы не можем предположить, что нулевые значения совпадают с более ранним моментом времени. Фактически в этом выражении положение y = 0 происходит в конце движения (точка 3), а не в начале (точка 1).
Как вы решали для Δt?
Чтобы найти Δt в этом уравнении, примите во внимание, что у вас есть квадратное уравнение: оно имеет вид a Δt 2 + b Δt + c = 0, где a = -4.9, b = 6,4 и c = 1,2. (Быстрый взгляд на единицы показывает, что Δt должно быть в секундах, поэтому я не буду переносить единицы измерения в алгебру для решения квадратного уравнения просто потому, что я хочу избежать путаницы, когда вы сосредотачиваетесь на математике.)
Решение квадратного уравнения дается как:
Обратите внимание, что квадратная формула всегда дает два решения. По сути, это формула для полной параболической дуги, и двумя решениями будут времена, когда объект находится на любой заданной высоте в этой дуге (один раз поднимается, а другой возвращается назад.) В этом случае мяч не был брошен с земли. Если бы он был брошен с земли (с такой скоростью, чтобы следовать по тому же пути), ему потребовалось бы 0,16 с, чтобы добраться от земли до вашей руки. Чтобы вернуться от руки к земле, требуется еще 1,5 секунды, а это именно та информация, которую вы хотите найти.
Мои числа близки, но не совсем те, которые показаны в уравнении. Достаточно ли я близок?
В тексте задачи приведены только две значащие цифры, поэтому в решение включены только две значащие цифры.
Какое ускорение у мяча? Откуда вы знаете?
В этой задаче вам явно предлагается игнорировать сопротивление воздуха. (Даже если это не так, сопротивление воздуха объектам, предназначенным для использования в качестве снарядов, движущихся с низкой скоростью, обычно довольно мало.) Следовательно, единственной существенной причиной ускорения мяча является сила тяжести. Для всех объектов у поверхности Земли ускорение силы тяжести g, направленное вниз, имеет значение 9.8 м / с 2 . (Если вы уже изучали силы, вы можете быстро увидеть это на диаграмме свободного тела.)
Как выбрать y = 0?
Все, что имеет значение для описания движения, — это то, что вы явно указываете, где находится ваша контрольная точка. В этом случае проблема давала высоту относительно земли, поэтому я выбрал точку отсчета. Если вы выбрали начальную точку (вашу руку) как y = 0, тогда земля будет на y = -1,2 м, а y 2 будет 2.1 мес. В любом случае вы получите одинаковые ответы.
Мяч был брошен прямо вверх. Почему вы показали это параболическим путем?
Это просто для удобства отображения всех трех точек на диаграмме. Точка 3 действительно находится прямо под точкой 1.
В моей книге используются такие переменные, как y, y
0 , v, v 0 и t. Почему вы используете 1, 2 и 3 в качестве индексов, а Δt вместо t?Кинематические уравнения связывают положение и скорость в любых двух точках движения.Поскольку многие задачи предоставляют или запрашивают информацию более чем в двух точках, я помечаю каждую точку своим собственным индексом, чтобы они оставались правильными.
 К выбору шариков нужно подойти серьезно, поскольку от этого зависит качество и прочность фигуры.
К выбору шариков нужно подойти серьезно, поскольку от этого зависит качество и прочность фигуры.
 ;
;

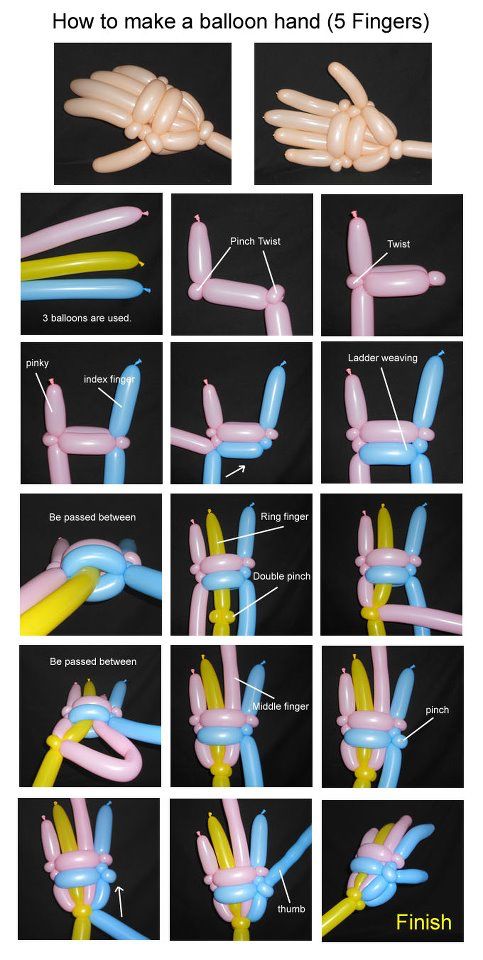 Причем не забывайте надувать их не до конца, оставляя пустой хвостик. Это необходимо для того, чтобы шарик не лопнул во время скручиваний. Чем сложнее ваши фигуры, тем больший хвостик нужно оставлять.
Причем не забывайте надувать их не до конца, оставляя пустой хвостик. Это необходимо для того, чтобы шарик не лопнул во время скручиваний. Чем сложнее ваши фигуры, тем больший хвостик нужно оставлять.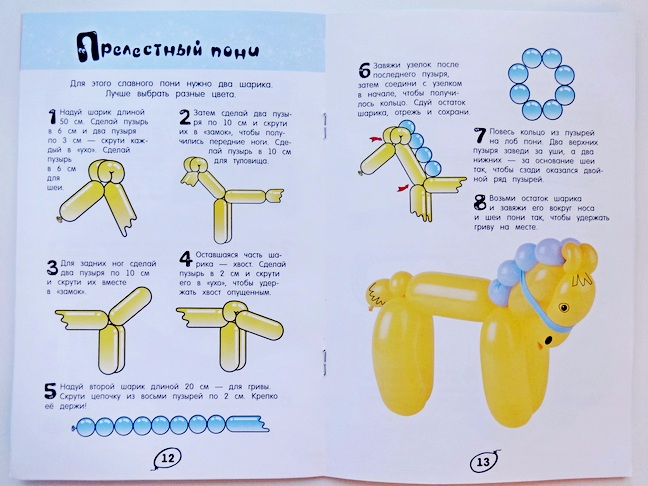 Обратите внимание, что если вы отпустите ее, она распрямится. Чтобы избежать этого, вам понадобится следующий прием.
Обратите внимание, что если вы отпустите ее, она распрямится. Чтобы избежать этого, вам понадобится следующий прием.
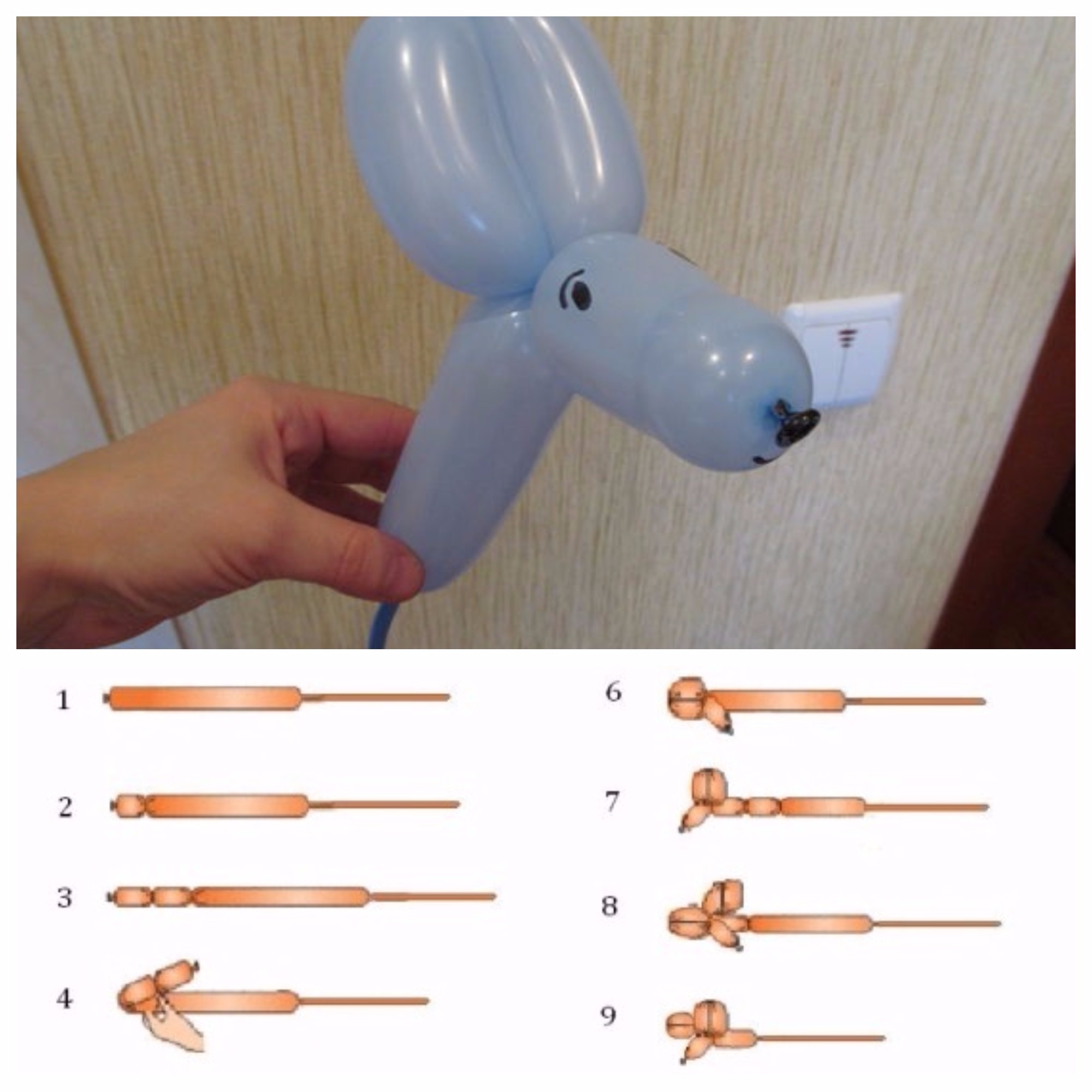
 Сразу выполните складывающуюся скрутку длиной около 10 см. Это первый лепесток.
Сразу выполните складывающуюся скрутку длиной около 10 см. Это первый лепесток.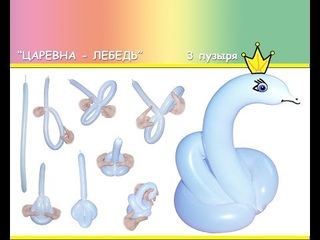
 Теперь со стороны узелка отступите на 5 сантиметров и сделайте 5-6 оборотов, чтобы получилась «колбаска». Таким же образом сделайте еще две колбаски, но немного меньшего размера (3-4 сантиметра). Первая будет служить мордочкой собачки, а две других – ушками.
Теперь со стороны узелка отступите на 5 сантиметров и сделайте 5-6 оборотов, чтобы получилась «колбаска». Таким же образом сделайте еще две колбаски, но немного меньшего размера (3-4 сантиметра). Первая будет служить мордочкой собачки, а две других – ушками. Вот и все, что необходимо для того, чтобы сделать собачку из шарика, как просто, не правда ли?
Вот и все, что необходимо для того, чтобы сделать собачку из шарика, как просто, не правда ли?
