Как сделать выпуклый круг из бумаги: Как сделать объемный круг из бумаги

Как сделать объемный круг из бумаги

Для декорирования интерьера часто используют объемные круги из бумаги. Как сделать праздничное оформление помещения своими руками? Мастера используют самые разные виды бумаги. Это и тонюсенькая папиросная, из которой легко сделать шары-соты, и более плотная цветная — для изготовления шаров, сложенных из множества кружков одинакового размера.

Можно готовые поделки повесить в виде гирлянды на Новый год или для поздравления именинника, закрепить на разных уровнях над окном или под потолком. Из гофрированных веерных кругов интересно делать цветочные объемные композиции из бумаги. Круги легко выполнить простым складыванием листа «гармошкой», поэтому создать красивый объемный цветок смогут даже дети дошкольного возраста. Их можно сделать ребристыми или надрезать края полукругом или острыми уголками, тогда круг предстанет в новом облике. Разнообразить поделки можно, используя разную цветовую гамму, варьируя надрезы на краях или добавляя контрастные сердцевины.

В статье рассмотрим несколько самых простых вариантов того, как сделать объемный круг из бумаги. Пошаговое описание выполнения работы поможет справиться с заданием намного проще и сделать поделку быстрее и качественнее. Готовый результат работы мастеров внимательно рассмотрите на представленных фотографиях.

Поделка из множества кругов

Из плотной цветной бумаги нарежьте большое количество одинаковых кругов. Можно использовать один цвет материала или все элементы выполнить разноцветными. Затем предстоит каждую деталь сложить пополам и хорошо загладить сгиб. Один кружок оставьте целым. На него, как на основу, будет выполняться поэтапное наклеивание элементов объемного круга из бумаги. Как сделать такую поделку? Очень просто! При сборке клей наносится только на одну, нижнюю половину каждого кружка. Верхняя часть остается свободной и придает поделке объемности.

При наклеивании деталей острый угол полукруга должен касаться центральной точки основания. Остальные поочередно вставляются внутрь со сдвигом на одинаковое расстояние. Середину оформляют пуговицей, бусинами или камушками.

Гофрированные объемные круги

На видео ниже в статье показано изготовление объемного круга из бумаги своими руками. Если вы из получившегося изделия хотите сделать цветок, то по центру веерного круга наклейте плотный кружок из картона и украсьте его кусочками гофрированной бумаги так, как показывает мастер в видео.

Как видите, работу выполнить просто, к тому же ее можно разнообразить, оформляя края сложенной «гармошкой» бумаги по своему вкусу.

Шары для гирлянды

Давайте рассмотрим, как сделать объемный круг из бумаги для новогодней гирлянды. В качестве материала желательно выбирать плотную бумагу, чтобы края кружочков не скручивались и не портили внешний вид поделки. Нарисуйте с помощью циркуля шаблон на картоне и, приложив к сложенной в несколько раз бумаге, обведите его контуры простым карандашом. Таким образом вы сможете вырезать сразу много одинаковых элементов.

Можно сделать объемный круг из кружков разных цветов, тогда гирлянда получится пестрая и более яркая. Каждый элемент нужно согнуть пополам и разгладить сгиб бумаги пальцами или линейкой. Потом одну половинку намазывают клеевым карандашом и приклеивают к половине второго элемента. Когда наклеено много деталей, соедините первую деталь с последней, предварительно вовнутрь вставив нитку или ленту.

Изготовление шаров-сот

Такую поделку лучше всего делать из папиросной тонкой бумаги, хотя некоторые делают шары-соты из двусторонней цветной бумаги. В нашем образце показано выполнение первого варианта, то есть из большого количества одинаковых тонких прямоугольников. Для начала нужно сделать расчерченный шаблон на плотном листе картона двумя маркерами разного цвета, располагая линии на равном расстоянии поочередно. Для удобства и шаблон, и первый лист крепят на основу малярным скотчем, приклеивая его на углах.

Дальше нужно соединять между собой большое количество прямоугольников, наклеивая листы один на другой. Для этого намазывают тонкими полосками клей ПВА сначала по красным линиям шаблона, а на следующей детали рисуют полоски уже по синей разметке. Чем больше элементов, тем пышнее будет объемный круг. Должно быть не меньше 20 штук.

Последний этап работы

Когда вся подготовленная бумага нашла свое место в пачке, нарисуйте подходящий по размеру полукруг, приложите его к краю заготовки и обведите по контурам простым карандашом. Вырезают всю бумагу ножницами по намеченной линии.

Остается нарисовать клеем недостающие линии и соединить между собой первый и последний полукруг. Чтобы можно было шары-соты повесить на нитке, перед сборкой вставьте петельку вовнутрь и закрепите ее клеем. Обязательно промажьте боковой стык, чтобы шар держал хорошо круглую форму.

Чем больше размер объемного круга, тем больше нужно рисовать полосок клеем. Маленький шар можно сделать из более плотной бумаги, рисуя по очереди только центральную линию полукруга клеем, а на следующей детали поставьте 2 линии, удаленные к краям на равном расстоянии от центра.

Мы познакомили читателей с несколькими популярными вариантами того, как сделать из листа бумаги объемные круги. Как видите, это несложно. Главное, захотеть создать самостоятельно красивую поделку. Пробуйте, у вас обязательно получится!

Как сделать круг из бумаги?

• Как сделать новогодний шар из бумаги?
• Как сделать шар из разноцветной бумаги?
• Как сделать шар из гофрированной бумаги?
• Как изготовить шар кусудама в технике оригами?
• Как еще сделать шар в технике кусудама?
• Как сделать яркий шар по шаблону?
• Как сделать шарик в виде цветочков?
• Как сделать бумажный шар из полосок?
• Как сделать шар из папье-маше?
• Видеоматериал

Из бумаги можно изготовить огромное количество поделок. Самым простым, интересным и познавательным изделием является шар. Конструировать такую фигуру легко и очень захватывающе. Довольно удивительным является то, что бумага является плоской, а фигура получается объемной. Существует много способов проектирования занимательного изделия. В данной статье мы рассмотрим, как сделать круг из бумаги своими руками.

к содержанию ↑

Как сделать новогодний шар из бумаги?

Рассмотрим, как самостоятельно изготовить объемный новогодний шар.

Материалы для работы:

• белый лист бумаги;
• предварительная подобранная цветная бумага;
• клей-карандаш или жидкий клей;
• ножницы для бумаги.

Мастер-класс

Для того чтобы изготовить объемный новогодний шар, необходимо произвести такие действия:

1. На принтере распечатываем два экземпляра шаблона как на цветной, так и на  белой бумаге.   
2. Используя ножницы, вырезаем шаблоны и раскладываем их по принципу “солнышка”.
3. Вырезанный кружок обрабатываем клеем и приклеиваем в середину, лучики при этом должны быть соединены в одной точке.
4. Начинаем формировать шар. Цветной шаблон должен находиться на белом. Первое действие — переплетение белых лучиков с цветными.
5. Далее получается композиция, при которой белые лучи оказываются сверху цветных. Теперь их опять прячем под лучи другого цвета.
6. В завершении процесса соединяем лучи и вместе производим их закрепление в одной точке.

к содержанию ↑

Как сделать шар из разноцветной бумаги?

Чтобы самостоятельно сконструировать самую простую фигуру в форме объемного круга из бумаги, понадобится применить стандартный канцелярский набор:

• бумага — лучше всего использовать разноцветные блоки квадратной формы, которые служат для различных записей;   
• ножницы для бумаги;
• клей-карандаш или жидкий клей;
• кружка или какой-нибудь другой предмет, имеющий круглое дно;
• циркуль с карандашом.

Мастер-класс

Чтобы сделать круг из разноцветной бумаги:

• Из подготовленных листов бумаги вырезаем круги с соответствующим диаметром около 10 см. Для того чтобы сконструировать объемный шарик, нам понадобится 32 круга двух цветов — 16 фигурок одного оттенка и 16 другого.
• Для того чтобы вырезанные заготовки были аккуратными и идеально круглыми, необходимо воспользоваться деталью круглой формы, например, обычной кружкой или основанием конфетницы. По ободку выбранного предмета вычерчиваем контур на каждом круге. Если нет подходящего предмета, можно применить циркуль и вычертить окружность нужного диаметра.

Важно! Если вы заинтересованы сэкономить свое время, то достаточно нарисовать на первом листе окружность и вырезать первый круг. Затем по данному шаблону вырезаем все остальные заготовки.

• Каждую получившуюся фигуру сгибаем пополам.
• Начинаем склеивать элементы друг с другом. Обрабатываем клеем верхнюю наружную половинку желтой заготовки, приклеиваем ее на нижнюю наружную часть красного круга.
• Точно по такой же схеме склеиваем друг с другом все вырезанные фигурки, при этом чередуем цвета: красная заготовка — желтая деталь — опять красный круг — желтый элемент. В результате — получается склеенная между собой стопка листов, имеющих полукруглую форму, которая немного напоминает книгу или журнал.
• Разворачиваем склеенное изделие и переходим к следующему этапу — соединению разноцветных “страниц” шара друг с другом.

Важно! Необходимо обратить внимание на то, что “страницы” разных цветов соединяются по разной схеме.

• Начинаем склеивать красные “страницы”. Раскрываем красный круг и мысленно делим заготовку на 6 секторов. Нижний и верхний сектор левого полукруга обрабатываем клеем, средний при этом остается нетронутым.
• Затем склеиваем их, присоединив при этом первый и третий сектор правого полукруга. После полного высыхания клея получается заготовка, похожая на “карман”.
• Точно так же склеиваем все красные “страницы” будущего шара.
• Далее начинаем соединять желтые “страницы”. Разворачиваем одну из желтых заготовок и обрабатываем клеем самую выступающую часть, которая является вторым сектором левого полукруга. Затем склеиваем с симметрично расположенным элементом правого желтого круга.
• Точно таким же образом поступаем со “страницами” желтого цвета.
• Будущий шар опять складываем “книжкой” и оставляем до полного высыхания клея.
• Далее разворачиваем склеенную деталь веером и проверяем, чтобы все “страницы” были правильно соединены.
• Из нитки изготавливаем петлю и при помощи клея соединяем первую и последнюю “страницы книжки”, таким образом формируется объемный шар.
• Даем будущей фигуре полностью высохнуть.

Желтый объемный шар с сердцевиной красного цвета готов!

Важно! Если изменить место склеивания разноцветных “страничек”, то можно создать новые варианты бумажного изделия. Такая модель шара может стать прекрасной основой для воплощения в жизнь оригинальных елочных украшений и интерьерных гирлянд.

к содержанию ↑

Как сделать шар из гофрированной бумаги?

Можно спроектировать шар из гофрированной бумаги, который будет иметь невесомый, воздушный и похожий на цветок вид.

Материалы

Для изготовления необходимо подготовить следующие материалы:

• листы гофрированной бумаги в количестве 5 штук с соответствующими размерами 40 на 60 см;
• проволоку;
• нить;
• фигурные ножницы;
• ножницы для бумаги.

Мастер-класс

Чтобы сделать объемный круг из гофрированной бумаги:

1. Гофрированную бумагу складываем гармошкой, или можно просто свернуть в рулон. От того, насколько большое будет количество лепестков, будет зависеть объемность будущего шара. Для этого свернутый рулон должен быть как можно толще при небольшой ширине загиба.
2. Нитью или проволокой скрепляем “гармошку” посередине.
3. Формируем лепестки, применяя фигурные ножницы и вырезая обе торцевые стороны изготовленной “гармошки”.
4. Аккуратно разворачиваем ваше изделие.
5. Расправляем лепестки по разным сторонам, чтобы получилась оригинальная,  объемная и воздушная фигура.  

Важно! Получившийся шар можно применять как украшение для домашнего интерьера или в качестве декоративного атрибута для любого торжества — дня рождения, выпускного праздника или свадебной церемонии.

к содержанию ↑

Как изготовить шар кусудама в технике оригами?

Кусудама является объемной шарообразной фигурой, при сборке которой применяется большое количество оригамных модулей. Много веков назад такая техника складывания кусудам зародилась в Японии. Композиция, состоящая из бумажных цветов, выполненная в форме шара, является одним из вариантов кусудамы. При этом существует огромное множество вариаций компоновки составных частей такого изделия. Изготовление шара в подобной технике не настолько сложная работа, как может показаться с первого раза. Главное условие данного искусства — это иметь терпение в работе.  

Материалы

Для того чтобы спроектировать необычное объемное изделие из цветов, необходимо подготовить:

• цветную бумагу;
• ножницы для бумаги;
• клей — карандаш;
• простой карандаш;
• линейку.

Мастер-класс

Чтобы сделать объемный круг кусудама из бумаги в технике оригами своими руками:

1. Заранее подготовленную бумагу нарезаем на квадратные заготовки со сторонами около 7-8 см. Всего необходимо вырезать 60 таких квадратов. В конечном итоге у вас получится 12 соцветий, каждый из которых состоит из пяти листков.
   Цветовая гамма квадратов при этом может быть различной.
2. Вырезанный квадрат складываем вдвое по диагонали от себя. Углы образовавшегося треугольника загибаем наверх таким образом, чтобы образовался ромб.
3. Отогнутые ранее треугольники аккуратно “расплющиваем”.
4. Далее верхние части будущих лепестков отгибаем вниз.
5. Теперь каждый из лепестков складываем пополам в направлении центра.
6. Соединяя крайние точки лепестков друг с другом, складываем модуль пополам.
7. Склеиваем клеем края лепестков между собой и таким образом создаем первую деталь будущего шара.
8. Точно по такой же схеме складываем еще 4 точно таких же модуля, после чего соединяем их при помощи клея-карандаша. В результате — образуется объемная деталь, имеющая форму соцветия.
9. По такому же принципу оформляем еще 11 цветочных деталей. После этого аккуратно присоединяем их друг к другу и склеиваем между собой.

Важно! Если шар будет находиться в подвешенном состоянии, то когда вы скрепите между собой несколько модулей, необходимо внутри закрепить шнур, при помощи которого изделие будет висеть.

Яркий объемный шар кусудама из бумаги готов!

к содержанию ↑

Как еще сделать шар в технике кусудама?

Существует еще один вариант изготовления объемной фигуры с применением искусства кусудама. Для создания подобной фигуры потребуется минимальное количество материалов:

• лист цветной бумаги;
• ножницы для бумаги.

Как сделать круг из бумаги в технике кусудама:

1. Из листов бумаги вырезаем шесть квадратов.
2. Намечаем две диагонали.
3. Намечаем две линии.
4. Складываем все углы к центру, затем разворачиваем обратно.
5. К центральной линии складываем боковые стороны квадрата сгибом вниз.  
6. Выполняем две складки сгибом вниз.
7. Аккуратно вытаскиваем изнутри четыре угла и расправляем их.
8. Раскрываем и расправляем каждый треугольник.
9. Отгибаем углы сгибом вверх, таким образом оформляется одна деталь кусудамы.
10. Точно так же создаем еще пять таких заготовок и склеиваем их отогнутыми уголками.

Объемный шар в технике кусудама готов!

к содержанию ↑

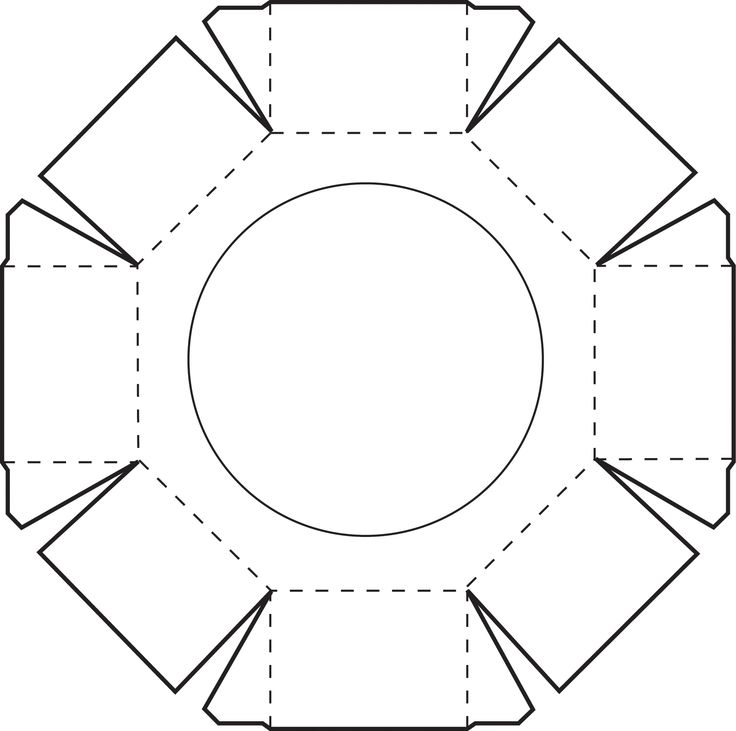
Как сделать яркий шар по шаблону?

Рассмотрим еще один вариант проектирования шара своими руками.

Материалы

Для того чтобы изготовить такую яркую и объемную фигуру необходимо предварительно подготовить следующие материалы:

• бумага ярких цветов;
• распечатать на принтере шаблон,
• простой карандаш;
• скотч;
• иголка с ниткой;
• клей;
• веревочка для петельки;
• ножницы для бумаги.

Изготовление круга — инструкция

Чтобы сделать объемный круг из бумаги:

1. Прикладываем распечатанный на принтере шаблон к листу цветной бумаги, обводим простым карандашом и вырезаем по намеченной линии.
2. Делаем прорези в местах, помеченных черной линией.
3. Такими образом вырезаем 12 цветных заготовок.

Дальше приступаем к сборке будущего изделия. Для этого необходимо определиться с вариантом использования:

• Если изготовленный шар будет висеть, то на первой заготовке следует прикрепить при помощи скотча веревку. Скотч сначала приклеиваем на обратную сторону детали, а затем протыкаем иголкой отверстие, что не позволит бумажной фигуре порваться.

Важно! Хвостики веревки также можно приклеить.

• Если ваш объемный шар из бумаги будет находиться на какой-то твердой горизонтальной поверхности, то без закрепления веревочки можно сразу приступить к сборке будущего изделия.  

При помощи прорезанных линий в каждой заготовке, скрепляем все шаблоны вместе. Объемный яркий шар готов!

к содержанию ↑

Как сделать шарик в виде цветочков?

Можно очень легко и быстро создать объемный шарик в виде цветочков по шаблону.

Материалы

Для этого подготавливаем следующие материалы:

• шаблон;
• листы цветной бумаги;
• клей;
• ножницы для бумаги;
• веревочка для петельки

Инструкция по сборке

Рассмотрим процесс изготовления цветочного шарика:

1. По предварительно распечатанному на принтере шаблону вырезаем 8 кругов одинакового диаметра.
2. Сворачиваем 3 края таким образом, чтобы образовался равносторонний треугольник.
3. С каждой стороны заготовки прорезаем наполовину линии.
4. Скрепляем все заготовки вместе.
5. Приклеиваем из веревочки петельку.

Интересный шарик в виде цветочков из бумаги готов!  

к содержанию ↑

Как сделать бумажный шар из полосок?

Очень интересный и очень простой вариант изготовления шара из бумажных полосок.

Материалы

Для этого вам потребуются следующие материалы:

• листы цветной бумаги;
• клей;
• скотч;
• ножницы для бумаги.

Инструкция по созданию поделки

Как сделать объемный круг из полосок бумаги своими руками:

1. Из листа цветной бумаги вырезаем полоски одинаковой длины. Количество полосок вы выбираете сами. Если для работы применить разноцветные полоски, цветовая гамма которых прекрасно гармонирует между собой, то можно создать очень оригинальное изделие.
2. Оформляем из полоски колечко и закрепляем его скрепкой или клеем.
3. Перпендикулярно первому кольцу формируем второе колечко.
4. Оставшиеся полоски закрепляем между собой аналогичным способом.

Шарик из полосок готов. При желании его можно дополнительно украсить всевозможными блестками, наклейками, бусинами.

к содержанию ↑

Как сделать шар из папье-маше?

Также можно сконструировать шарик из папье-маше.

Материалы

Для создания подобного изделия подготавливаем необходимые материалы и инструменты:

• воздушный шарик;
• не цветные газеты;
• жидкий клей;
• кисточка для клея;
• нить;
• бумага;
• ножницы для бумаги.

Подробный мастер-класс

Рассмотрим процесс изготовления объемного шара в технике папье-маше:

• Заполняем воздухом надувной шар таким образом, чтобы он стал идеально круглым.
• Измельчаем газету.
• Обклеиваем шарик кусочками газеты, пропустив при этом хвостик.

Важно! Лучше всего шарик оформить 2-3 слоями. Последний слой должен состоять из листов обычной бумаги белого цвета.

• Оставляем изделие, чтобы оно смогло высохнуть.
• После полного высыхания иголкой аккуратно прокалываем воздушный шар и достаем его части.
• Прикрепляем нитку.

Шар из папье-маше готов! По желанию изделие можно разрисовать и украсить дополнительными элементами.

к содержанию ↑

Видеоматериал

Даже такую простую поделку, как круг из бумаги, можно сделать сотнями способов. В этой статье мы предложили вам лишь несколько наиболее простых и удачных на наш взгляд. Опробовав такие техники, вы можете продолжать совершенствовать свои навыки, привнося в декоративное оформление комнат на праздники новые нотки вашей фантазии.

Как сделать многогранник из бумаги) « Math Craft :: WonderHowTo

• org/Person»> Автор Кори Пул
• 9.10.11 17:25
• 04.11.11 8:34

Добро пожаловать в мир математики! Это сообщество посвящено изучению искусства и архитектуры, вдохновленных математикой, с помощью проектов, материалов сообщества и вдохновляющих сообщений, связанных с рассматриваемой темой. Каждую неделю будет примерно четыре поста по следующему расписанию:

• Понедельник : Основные моменты, представленные участниками на пробковой доске сообщества.
• Вторник : Знакомство с новым проектом недели.
• Четверг : Расширения, вдохновение и другие математические детали для текущего проекта недели.
• Пятница : Вдохновляющие посты о художниках и произведениях искусства в этой области, включая исторические проекты и работы.

Моя цель — организовать общественный форум, на котором люди могут учиться, участвовать и вносить свой вклад. С учетом сказанного, пожалуйста, опубликуйте что-нибудь актуальное в разделе комментариев к сообщениям, на пробковой доске сообщества или создайте тему на форуме. Я надеюсь, что сообщество узнает друг от друга еще больше, чем из моих постов.

Так как это первый пост, а будущие понедельники будут посвящены представлению материалов сообщества, я собираюсь отойти от графика и поделиться простым проектом «Сделай сам» для изучения основ геометрического искусства.

Бумажные многогранники

Многогранники — это трехмерные расширения двумерных многоугольников. Они полностью состоят из плоских граней и прямых краев. Поскольку они полностью состоят из плоских граней с прямыми краями, их часто можно развернуть в двухмерную форму, как картонную коробку. Эта развертка многогранника называется сеткой. Один из самых простых способов сделать трехмерную фигуру — сделать сетку из бумаги и сложить ее.

Чтобы показать, какие удивительные формы можно делать из бумаги, используя методы, похожие на складывание сетей, я представляю несколько изображений работы отца Магнуса Веннингера.

Это поистине удивительные геометрические фигуры. Объекты последней группы на самом деле являются трехмерными проекциями или тенями объектов, которые могут существовать только в четырех измерениях! Когда-нибудь, возможно, мы подробно рассмотрим эти полихороны.

А пока давайте посмотрим на сетки для складывания простых бумажных геометрических объектов. У Gijs Korthals Altes есть отличный сайт для поиска этих сетей. Все, что вам нужно сделать, это загрузить объект, а затем использовать принтер, чтобы распечатать его на обычной бумаге или картоне. Затем вырежьте фигуру объекта и сложите его, как указано, а затем приклейте или заклейте объект скотчем.

Я предлагаю начать с Платоновых тел – простейших многогранников. Они полностью состоят из правильных многоугольников одинакового размера и формы и выпуклы, так что все углы изгибаются к центру формы. Шаблоны (сети) можно найти здесь. После того, как вы исчерпали платоновые тела, я предлагаю использовать архимедовы тела, которые могут иметь более одного типа многоугольника. Эти сети можно найти здесь.

Наконец, чтобы сделать по-настоящему крутые рождественские украшения, попробуйте несколько выпуклых многогранников, таких как многогранники Кеплера-Пуансо (скачать здесь). Обратите внимание, что это значительно сложнее и требует больше времени. Некоторые включают сотни складок. Большой икосаэдр, хотя и красивый, занял у меня почти 3 часа, чтобы вырезать и сложить из 1 листа бумаги.

Давайте рассмотрим процесс создания одного из них более подробно. Начнем с додекаэдра.

Материалы

• Что-то, чем можно резать (ножницы или нож Exacto).
• Коврик или доска для резки при использовании ножа Exacto.
• Бумага или картон. Я использую самые толстые листы, которые может выдержать мой принтер, поэтому я могу делать более прочные объекты, но это затрудняет их складывание. Карточки весом 110 фунтов можно купить в любом магазине канцелярских товаров. Обычно крупные розничные магазины, такие как Walmart или Target, продают более тонкий картон, что может быть предпочтительнее для некоторых из вас.
• Инструмент для надрезов, такой как пустая ручка или задняя часть столового ножа. Вам это действительно нужно, только если вы используете картон. На самом деле я просто слегка использую лезвие ножа Exacto, но это требует точности, поэтому будьте осторожны, если вы используете эту технику.
• Клей для рукоделия, гель-суперклей или лента.

Шаг 1 Загрузите, распечатайте и вырежьте

Перейдите на сайт загрузки и найдите многогранник, который хотите построить. Чтобы следовать за мной, перейдите в раздел о платоновых телах и скачайте шаблон додекаэдра. Я рекомендую файлы .pdf и обычно печатаю цветную страницу, а не раскрашиваю ее самостоятельно. Распечатайте сеть. Вырежьте его с помощью ножниц или ножа.

Убедитесь, что вы вырезали пространство между вкладками и другим многоугольником, которого он начинает касаться. Оставьте только вкладку, подключенную к основному полигону.

Шаг 2 Надрез

Если вы использовали картон, надавите биговкой на края и язычки, которые нужно согнуть. Это делает бумагу более слабой в этих местах, позволяя сгибам быть почти идеальными. Если вы использовали бумагу, бумага будет довольно легко складываться без этого шага. Это может помочь, но также может испортить бумагу, если вы не будете осторожны.

Шаг 3. Сложите и склейте

Сложите и склейте или приклейте скотчем объект. Обычно я частично сгибаю все края и выступы, чтобы видеть, как будет формироваться объект.

Нанесите клей на выступ, который вы хотите приклеить.

Прижмите язычок к многоугольнику, к которому он должен прикрепляться. Для суперклея нужно подержать всего пару секунд. Для других клеев вам, возможно, придется держать около минуты.

Повторяйте нанесение клея на выступы и прижимайте детали друг к другу, пока не закончите. Конечный объект должен выглядеть так:

Шаг 4 Готово!

А теперь иди и поиграй со своей растущей коллекцией многогранников. Придумайте способы их использования в других проектах. Возможно, вы могли бы использовать их в качестве рождественских украшений. Получайте удовольствие и размещайте результаты на пробковой доске!

Вот мой: В эти выходные я решил использовать многогранники, чтобы сделать мобиль для моего новорожденного сына. Вот краткое изображение того, что я сделал, используя бумажные многогранники, несколько медных трубок диаметром 1/4 дюйма и немного медной акустической проволоки.

Наконец, вот мой самый полезный совет: не слишком расстраивайтесь. Некоторые из вас смогут сделать это легко сразу. Другим может потребоваться довольно много времени, чтобы создать что-то похожее на то, что сделал ребенок начальной школы. Ваши руки могут быть покрыты клеем. Это нормально. Как и все остальное, это может потребовать некоторой практики. Это было для меня. Веселиться. И знайте, что это вызывает привыкание. Вы можете получить дом, квартиру или комнату в общежитии, полностью заполненную ими.

Во вторник научимся делать многогранники из обычных игральных карт вот так:

Хотите освоить Microsoft Excel и поднять перспективы работы на дому на новый уровень? Начните свою карьеру с нашего учебного комплекта Microsoft Excel Premium от А до Я в новом магазине Gadget Hacks Shop и получите пожизненный доступ к более чем 40 часам базовых и продвинутых инструкций по функциям, формулам, инструментам и многому другому.

Купить сейчас (9Скидка 7 %) >

Другие интересные предложения:

• Скидка 97 % The Ultimate 2021 White Hat Hacker Certification Bundle
• Скидка 98 % The 2021 Accounting Mastery Bootcamp Bundle
• Скидка 99 % Allin-2021 -One Data Scientist Mega Bundle
• Скидка 59 % на XSplit VCam: пожизненная подписка (Windows)
• Скидка 98 % на сертификационный комплект Premium Learn To Code 2021
• Скидка 62 % Программное обеспечение MindMaster Mind Mapping: бессрочная лицензия
• Скидка 41 % на анализатор NetSpot Home Wi-Fi: бессрочные обновления

31 комментарий

• Горячий
• Последние

• Модульное оригами: Как сделать куб, октаэдр и икосаэдр из модулей Sonobe

• Как: Делаем 6-сторонние снежинки киригами

• Модульное оригами: Икосаэдр, октаэдр и куб

• Как: Создайте параболические кривые Используя прямые линии

• Как: Сделать гиперболический параболоид с помощью шпажек

• Как: Создавайте концентрические окружности, эллипсы, кардиоиды и многое другое с помощью прямых линий и окружностей

• Как: Превратите Платоновы Тела в игральные карты

• Модульное оригами: Как сделать усеченный икосаэдр, додекаэдр пентаки и многое другое

• Математическое ремесло понедельник: Материалы сообщества (плюс как сделать гиперболический параболоид в форме среза)

• Как: Сделать икосаэдрические украшения планет

• Праздничный проект: Новогодние елки оригами

• Новости: Лучший математический проект на свете

• Как: Сделать коробки для подушек Инь-Ян

• Новости: Фрактальная причудливость Сайриака Харриса

• Математическое ремесло понедельник: Материалы сообщества (плюс как сделать упорядоченный клубок треугольников)

• Новости: Рождественская елка Серпинского

• Математическое ремесло понедельник: Материалы сообщества (а также как сделать модульную скульптуру оригами из пересекающихся треугольников)

• Новости: 7 шаблонов для складывания геометрических конструкций из бумаги

• Математическое ремесло понедельник: Материалы сообщества (плюс как сделать ленты Мебиуса)

• Все функции

• Модульное оригами: Как сделать куб, октаэдр и икосаэдр из модулей Sonobe

• Как: Делаем 6-сторонние снежинки киригами

• Модульное оригами: Икосаэдр, октаэдр и куб

• Как: Создайте параболические кривые Используя прямые линии

• Как: Сделать гиперболический параболоид с помощью шпажек

• Как: Создавайте концентрические окружности, эллипсы, кардиоиды и многое другое с помощью прямых линий и окружностей

• Как: Превратите Платоновы Тела в игральные карты

• Модульное оригами: Как сделать усеченный икосаэдр, додекаэдр пентаки и многое другое

• Математическое ремесло понедельник: Материалы сообщества (плюс как сделать гиперболический параболоид в форме среза)

• Как: Сделать икосаэдрические украшения планет

• Праздничный проект: Новогодние елки оригами

• Как: Сделать коробки для подушек Инь-Ян

• Новости: Лучший математический проект на свете

• Новости: Фрактальная причудливость Сайриака Харриса

• Математическое ремесло понедельник: Материалы сообщества (плюс как сделать упорядоченный клубок треугольников)

• Новости: Рождественская елка Серпинского

• Математическое ремесло понедельник: Материалы сообщества (а также как сделать модульную скульптуру оригами из пересекающихся треугольников)

• Математическое ремесло понедельник: Материалы сообщества (плюс как сделать ленты Мебиуса)

• Новости: 7 шаблонов для складывания геометрических конструкций из бумаги

• Все горячие сообщения

Измерение выпуклости с помощью выпуклых многоугольников

Abstract

В этой статье описывается общий подход к вычислению семейства мер выпуклости. Вдохновленные использованием геометрических примитивов (таких как круги), которые часто подгоняются к формам для их аппроксимации, мы используем для этой задачи выпуклые многоугольники. Выпуклые многоугольники можно создавать разными способами, и здесь показаны некоторые из них. Эти многоугольники масштабируются и перемещаются, чтобы убедиться, что они соответствуют входной форме и дают значимую меру выпуклости. Впоследствии мера выпуклости может быть вычислена на основе степени перекрытия между двумя фигурами.

Ключевые слова

• Размер формы
• Выпуклость
• Классификация

Скачать документ конференции в формате PDF

1 Введение

Форма — это характеристика объектов, полезная как для биологического восприятия, так и для компьютерного зрения. линейность, округлость, выпуклость, эллиптичность, удлинение, компактность, линейность, сигмоидальность, извилистость и т. д. Хотя также существует множество подходов к измерению этих различных характеристик, несколько подходов обычно используются для различных характеристик формы. Например, формы, которые могут быть описаны параметрическими моделями, могут быть приспособлены к объекту, а ошибка подбора используется для количественной оценки принадлежности объекта к этому классу форм. Пример показан на рис. 1b, на котором окружность была установлена ​​для минимизации квадратов евклидовых ошибок точек данных. Такой подход привлекателен, поскольку подобранная модель представляет собой идеальный экземпляр модели, наиболее похожий на данные, и, следовательно, ошибки справедливо отражают отклонения от характеристики формы [1]. Другой популярный подход для простых геометрических моделей заключается в количественной оценке ошибки по отношению к описанной или вписанной модели, см. рис. 1c и d.

Рис. 1.

Различные подходы к подгонке окружностей к данным. (a) входная форма (b) приближение окружности к точкам данных методом наименьших квадратов (c) описанная окружность (d) вписанная окружность.

Изображение в натуральную величину

Выпуклость — это часто используемая характеристика формы, и было разработано множество показателей выпуклости (например, [2–10]). 7)\), см. [11]), в отличие от выпуклой оболочки, для которой существуют эффективные алгоритмы. Однако недостатком является то, что для форм, не близких к экземпляру идеальной модели, описанная/вписанная модель выпуклой оболочки не дает репрезентативного экземпляра модели, и поэтому ошибки в отношении этой модели не будут точно отражать характеристика формы.

Рис. 2.

Два подхода к подгонке выпуклых многоугольников к данным. (а) и (в) выпуклый корпус (б) и (г) выпуклый череп.

Изображение в натуральную величину

В качестве альтернативы выпуклой оболочке Розин и Мамфорд [8] описали две симметричные меры выпуклости, основанные на «робастифицированной» версии выпуклой оболочки, которая была определена как выпуклый многоугольник, максимизирующий свою перекрываются с входным полигоном. На рис. 3а видно, что этот многоугольник не описывает и не вписывает входную форму, а для примера с кругом он очень похож на подогнанный круг на рис. 1б. В этой статье мы представляем несколько альтернативных подходов, которые также создают выпуклые многоугольники, частично перекрывающие входной многоугольник (см. рис. 3b–f). Опять же, для примера с кругом они аналогичны подогнанному кругу на рис. 1b.

2 Новые меры выпуклости

Основной подход, использованный в этой статье для вычисления меры выпуклости:

1. 1.

   создать выпуклый многоугольник на основе входной формы; в данной работе представлено несколько вариантов;

2. 2.

   преобразовать выпуклый многоугольник так, чтобы он максимально соответствовал входной форме; в этой статье мы применили масштабирование таким образом, чтобы площади исходного и выпуклого многоугольников были одинаковыми, а также переместили многоугольники, чтобы максимизировать площадь их перекрытия;

3. 3.

   вычислить меру выпуклости; в этой статье мы использовали отношение площади перекрытия к площади входного полигона.

Рис. 3.

Некоторые альтернативные подходы к подгонке выпуклых многоугольников к данным. (a) Розин и Мамфорд (b) масштабированная выпуклая оболочка (c) сглаженный входной многоугольник (d) полигональное упрощение входного многоугольника (e) выпуклость (f) выпуклость с использованием расширенных поворотов. 9С\) : Естественный и эффективный способ вычисления выпуклого многоугольника — использовать выпуклую оболочку, см. рис. 2a и c.

Сглаживание — \(C_B\) : Известно, что если кривая сглаживается с помощью геометрического уравнения теплового потока, она становится все более и более круглой, в конечном итоге сжимаясь до круглой точки за конечное время [12]. Мы итеративно применяем сглаживание к входной форме, пока результат не станет выпуклым, см. рис. 3c. Поскольку данные были сильно сглажены, достаточно проверить выпуклость простым способом, проверив для кривой, упорядоченной против часовой стрелки, что в каждой вершине знак ее стягиваемого угла положительный. В качестве альтернативы можно использовать более сложные методы (например, оценку кривизны путем подгонки сплайнов [13]).

Полигональное упрощение — \(C_Y\) : Доступно множество алгоритмов. Мы используем подход оптимального динамического программирования [14], применяемый к версии контура с субдискретизацией, который достаточно эффективен и надежен. Это дает ломаную линию, содержащую n сегментов линии, и применяется двоичный поиск для нахождения выпуклого многоугольника с максимальным значением n , см. рис. 3d.

Выпуклость – \(C_F\) : Процесс многоугольной выпуклости был описан Паулем Эрдёшем [15, 16] и включает отражение вогнутостей многоугольника относительно соответствующих ребер в выпуклой оболочке. Повторение этого процесса приводит к выпуклому многоугольнику, который ранее использовался для измерения выпуклости [17]. Два таких выпуклых многоугольника показаны на рис. 3e.

Выпуклость с Flipturn– \(C_{FT}\) : Также рассматривалась модификация приведенной выше схемы, в которой вогнутости отражаются о полное ребро выпуклой оболочки, на которой расположена вогнутость, а также имеют обратный порядок их вершин («расширенный флип-поворот»). см. рис. 3f.

Для тех методов, которые создают выпуклый многоугольник путем увеличения входной формы (например, выпуклой оболочки или выпуклости), изменение масштаба, примененное на шаге 2, обеспечивает баланс между выступающими и выступающими неровностями. В противном случае этого нет в наиболее распространенных измерениях выпуклости площадь (S) / площадь (CH (S)) и периметр (CH (S)) / периметр (S), которые поэтому гораздо более чувствительны к выступам, чем к проникновениям.

Для сильно вогнутых форм может быть большая разница в площади между исходной формой и ее выпуклой оболочкой. Следовательно, когда выпуклая оболочка сжимается, чтобы соответствовать площади исходной формы, существует вероятность того, что она не будет пересекаться с исходной формой, что приведет к нулевому измеренному значению выпуклости. Поскольку нежелательно, чтобы мера выпуклости давала ноль (поскольку предполагается, что формы имеют ненулевую площадь), сжатая выпуклая оболочка перемещается, чтобы обеспечить перекрытие с исходной формой. Хотя можно было бы использовать более общие преобразования (например, вращение, аффинное с сохранением площади и т. д.), если рассматривать пример с выпуклой оболочкой, то перенос является минимальным преобразованием, которое дает разумную меру выпуклости. То есть никакая ненулевая форма площади не должна давать измеренную выпуклость, равную 0. Обычно наиболее целесообразно использовать самое простое и эффективное решение.

Параметры трансляции определяются по методу Пауэлла [18]. Чтобы гарантировать, что процесс оценки сходится даже в ситуациях, когда нет пересечения между сжатой выпуклой оболочкой и исходной формой, выпуклая оболочка сжимается постепенно (для всех наших данных было обнаружено, что 10 шагов достаточно). Затем оптимизация параметров перевода чередуется с итерациями сжатия. Эффективность оптимизации продемонстрирована на рис. 4.

рис. 4.

Мера выпуклости на основе выпуклой оболочки. Показаны четыре формы с увеличенным изгибом, а также их выпуклые оболочки или выпуклые оболочки с измененным масштабом. Под каждой фигурой показано ее измеренное значение выпуклости.

Изображение полного размера

3 Экспериментальные результаты

В этом разделе мы приводим несколько экспериментов, чтобы проиллюстрировать поведение и эффективность новых мер выпуклости, предложенных в этой статье.

3.1 Поражения

Первый эксперимент должен классифицировать 40 поражений как доброкачественные или злокачественные меланомы. Повреждения были оценены 14 дерматологами по четырехбалльной шкале в зависимости от вероятности того, что они являются меланомой. Ли и др.  [19] представили эти данные и ввели «общий индекс нерегулярности», который, как они показали, обеспечивает ранговую корреляцию Спирмена 0,88 по сравнению со средней экспертной оценкой. Ранее мы обнаружили, что меры выпуклости также хорошо справляются с этой задачей. Стандартная мера выпуклости выпуклой оболочки на основе площади \(C_A\) имела аналогичное значение корреляции 0,888, в то время как меры выпуклой оболочки Розина и Мамфорда [8] на основе выпуклой оболочки \(C_P\) и \(C_Q\) достигли высокого значения корреляции 0,958.

S\), \(C_F\) и \(C_{FT}\) накладываются друг на друга.

Изображение в натуральную величину

Таблица 1. Ранговая корреляция Спирмена предложенных показателей выпуклости по сравнению со средней экспертной оценкой вероятности того, что поражение является меланомой.

Полноразмерная таблица

На рис. 5 показаны два поражения, на которые наложены выпуклые многоугольники. Как показано в таблице 1, большинство новых мер выпуклости, предложенных в этой статье, также превосходят общий индекс неравномерности и приближаются к высокому значению корреляции, достигнутому мерами \(C_P\) и \(C_Q\) Розина и Мамфорда.

3.2 Гриблы

Далее мы повторяем эксперимент Розина и Мамфорда [8], в котором они вычислили выпуклость для набора из 1137 многоугольников, содержащих различные формы, а также 53 «гриблов». Последние представляют собой синтетические тестовые объекты, используемые в качестве стимулов в психологических тестах, и представляют собой формы, которые имеют качественно похожий внешний вид с некоторыми незначительными вариациями четырех выступов; два примера показаны на рис. 6. Меры выпуклости сравниваются путем упорядочения полного набора из 1137 многоугольников в соответствии с каждой мерой выпуклости. Вычисляется стандартное отклонение рангов Гребла, и низкие значения указывают на эффективность меры, поскольку это означает, что мера стабильна и непротиворечива при незначительных изменениях формы. Результаты показаны в таблице 2, и видно, что некоторые из новых мер выпуклости (в частности, \(C_B\)) по существу так же эффективны, как меры выпуклости, основанные на надежной выпуклой оболочке и выпуклом черепе (т. е. \( C_P\) и \(C_Q\)) [8]. 9S\), \(C_F\) и \(C_{FT}\) накладываются друг на друга.

Изображение в натуральную величину

Таблица 2. Показатели выпуклости, примененные к 1137 полигонам и ранжированные слева направо по стандартному отклонению грибловских рангов.

Полноразмерная таблица

3.3 Диатомовые водоросли

В этом эксперименте используются данные проекта ADIAC. 808 контуров были взяты из изображений диатомей (одноклеточных водорослей), происходящих из 38 таксонов (классов), которые были определены экспертом вручную. Доступны не только граничные контуры, но и орнаментация каждой диатомовой водоросли, которая состоит из нуля или более (в основном незамкнутых) участков кривой внутри — см. рис. 7. Ранее мы классифицировали эти данные, используя несколько мер выпуклости как по отдельности, так и в совокупности. сочетание со следующим набором дескрипторов [10]: округлость, эллиптичность, прямоугольность, треугольность [20] пропорции, компактность, выпуклость, эксцентриситет, первые четыре инварианта вращения, переноса и масштабного момента, четыре поворота, переноса и масштабного момента инварианты [21], первые три инварианта аффинных моментов [22]. Этот эксперимент был повторно проведен с использованием классификатора ближайшего соседа с расстояниями Махаланобиса и перекрестной проверкой с исключением одного, а не наклонными деревьями решений (как в [10]), и новая (улучшенная) точность классификации показана в верхней половине таблицы. 3. В нижней половине таблицы 3 показаны результаты классификации с использованием мер выпуклости, предложенных в этой статье. Можно видеть, что эффективность двух наборов мер выпуклости аналогична: хотя любая отдельная мера выпуклости имеет низкую скорость классификации, она значительно повышается в сочетании с (одной) внутренней мерой выпуклости и еще более существенно увеличивается, когда добавлены 14 общих дескрипторов формы. Дальнейшее улучшение достигается путем объединения общих дескрипторов формы с внутренней мерой выпуклости \(C_J(I)\) и новой мерой выпуклости на основе границы \(C_{FT}\) для получения 91,58 %.

Рис. 7.

Внешняя граница и внутренние контуры образцов диатомей разных таксонов.

Изображение в натуральную величину

Таблица 3. Процентная точность классификации 808 диатомовых водорослей с 38 классами с использованием выпуклости плюс дополнительные общие меры формы.

Полноразмерная таблица

Интересно отметить, что хотя различные меры выпуклости номинально измеряют одну и ту же характеристику формы, на самом деле они охватывают разные аспекты выпуклости. Таким образом, при совместном использовании различные меры выпуклости предоставляют независимую информацию, которая позволяет их комбинации превзойти любую индивидуальную меру выпуклости. Меры выпуклости, ранее проверенные Жуничем и Розином [10], а именно \(C_A\), \(C_L\), \(C_J(B)\) и \(C_J(I)\), в совокупности обеспечивают точность 62,13 %. , трехкратное увеличение отдельных мер выпуклости. Если объединить старые и новые меры выпуклости, 9S\), \(C_F\) и \(C_{FT}\), то скорость классификации увеличивается до 77,48 %.

4 Заключение

В этой статье мы описали новый подход к вычислению семейства мер выпуклости. Процедура включает (1) создание выпуклого многоугольника, (2) подгонку выпуклого многоугольника к входной форме путем применения масштабирования и переноса и (3) вычисление меры выпуклости на основе входной формы и выпуклого многоугольника.

Было продемонстрировано несколько конкретных примеров этого подхода с использованием выпуклой оболочки, сглаживания, выпуклости и т. д. для создания выпуклого многоугольника, в то время как для меры выпуклости мы использовали отношение площади перекрытия двух фигур к площади входной полигон. Более того, для каждого из этих двух шагов существует множество дополнительных возможностей, что еще больше увеличивает количество мер выпуклости, которые можно сгенерировать.

Результирующие меры выпуклости обладают желаемыми свойствами, заключающимися в том, что только выпуклые формы имеют измеренную выпуклость, равную 1, и что никакая форма с ненулевой площадью не должна давать измеренную выпуклость, равную 0.

Эксперименты показали, что предложенные меры выпуклости эффективны для классификации, и что несколько мер выпуклости можно комбинировать друг с другом и с мерами невыпуклости для улучшения показателей классификации.

Примечания

1. 1.

   Включение \(C_A\) со всеми другими мерами выпуклости привело к небольшому падению точности до 76,61 %.

Ссылки

1. Нил, Ф., Расс, Дж.: Измерение формы. Тейлор и Фрэнсис, Бока-Ратон (2012)

   CrossRef МАТЕМАТИКА Google ученый

2. Боксер, Л.: Вычисление отклонений от выпуклости в многоугольниках. Распознавание образов лат. 14 , 163–167 (1993)

   CrossRef МАТЕМАТИКА Google ученый

3. Corcoran, P., Mooney, P., Winstanley, A.C.: Мера выпуклости для открытых и замкнутых контуров. В: Труды Британской конференции по машинному зрению, стр. 1–11 (2011 г.)

   Google ученый

4. Какарала, Р.: Проверка выпуклости с помощью дескрипторов Фурье. Электрон. лат. 34 , 1392–1393 (1998)

   CrossRef Google ученый

5. Мартин Р., Розин П.: Превращение проблем принятия решений в измерения. Междунар. J. Модель формы. 10 , 83–113 (2004)

   CrossRef МАТЕМАТИКА Google ученый

6. Пао, Х., Гейгер, Д., Рубин, Н.: Измерение выпуклости для разделения фигуры и фона. В: Международная конференция по компьютерному зрению, стр. 948–955 (1999)

   . Google ученый

7. Рахту, Э., Сало, М., Хейккиля, Дж.: Новая мера выпуклости, основанная на вероятностной интерпретации изображений. IEEE транс. Анальный узор. Мах. Интел. 28 , 1501–1512 (2006)

   CrossRef Google ученый

8. Розин, П., Мамфорд, К.: Симметричная мера выпуклости. вычисл. Вис. Изображение Понимание. 103 , 101–111 (2006)

   CrossRef Google ученый

9. Стерн Х.: Полигональная энтропия: мера выпуклости. Распознавание образов лат. 10 , 229–235 (1989)

   CrossRef МАТЕМАТИКА Google ученый

10. Жунич, Дж., Розин, П.: Новое измерение выпуклости многоугольников. IEEE транс. Анальный узор. Мах. Интел. 26 , 923–934 (2004)

    CrossRef Google ученый

11. Чанг Дж., Яп К.: Полиномиальное решение задачи очистки картофеля. Дискретный вычисл. геом. 1 , 155–182 (1986)

    CrossRef MathSciNet МАТЕМАТИКА Google ученый

12. Грейсон, М.: Уравнение теплопроводности сжимает вложенные плоские кривые в круглые точки. Дж. Дифференц. геом. 26 , 285–314 (1987)

    CrossRef MathSciNet МАТЕМАТИКА Google ученый

13. Козера, Р., Ноукс, Л.: Гладкая интерполяция с кумулятивными кубическими хордами. вычисл. Вис. График 32 , 87–94 (2006)

    CrossRef МАТЕМАТИКА Google ученый

14. Перес, Дж., Видаль, Э.: Оптимальная полигональная аппроксимация оцифрованных кривых. Распознавание образов лат. 15 , 743–750 (1994)

    CrossRef МАТЕМАТИКА Google ученый

15. Айххольцер О., Кортес К., Демен Э., Дуймович В., Эриксон Дж., Мейер Х., Овермарс М., Палоп Б., Рамасвами С., Туссен , Г.: Переворачивание многоугольников. Дискретная вычислительная геометрия. 28 , 231–253 (2002)

    CrossRef MathSciNet МАТЕМАТИКА Google ученый

16. «>

    Erdös, P.: Задача № 3763. Амер. Мат. Ежемесячно 42 , 627 (1935)

    Перекрестная ссылка MathSciNet Google ученый

17. Розин, П.: Классификация патологических форм с использованием показателей выпуклости. Распознавание образов лат. 30 , 570–578 (2009)

    CrossRef Google ученый

18. Press, W., Flannery, B., Teukolsky, S., Vettering, W.: Numerical Recipes in C. Cambridge University Press, Cambridge (1990)

    Google ученый

19. Lee, T., McLean, D., Atkins, M.: Индекс неровности: новый показатель неровности границ для кожных поражений. Мед. Анальный образ. 7 , 47–64 (2003)

    CrossRef Google ученый

20. Розин, П.: Измерение формы: эллиптичность, прямоугольность и треугольность. Мах. Вис. заявл. 14 , 172–184 (2003)

    CrossRef Google ученый

21. Сонка М., Главац В., Бойл Р.: обработка изображений, анализ и машинное зрение. Томсон-Инжиниринг, Торонто (2007 г.)

    Google ученый

22. Флюссер Дж., Сук Т.: Распознавание образов с помощью инвариантов аффинных моментов. Распознавание образов 26 , 167–174 (1993)

    CrossRef MathSciNet Google ученый

Скачать ссылки

Благодарность

Эта работа частично поддерживается Министерством науки Республики Сербии, проекты OI174008/III044006.

Информация об авторе

Авторы и организации

1. Школа компьютерных наук и информатики Кардиффского университета, Кардифф, Великобритания

   Йовиша Жунич

Авторы

1. Paul L.