Многоугольник с 5 сторонами фото: Как выглядит пятиугольник фото
Как выглядит пятиугольник фото
Содержание
- Содержание
- Свойства [ править | править код ]
- Построение [ править | править код ]
- Получение с помощью полоски бумаги [ править | править код ]
- В природе [ править | править код ]
- Параметры правильного пятиугольника
- Построение пентагона
- Интересные факты
- Видео
- Как выглядит пятиугольник и звезда
| Пятиугольник | |
|---|---|
Правильный пятиугольник | |
| Тип | Правильный многоугольник |
| Рёбра | 5 |
| Символ Шлефли | |
| Диаграмма Коксетера — Дынкина | |
| Вид симметрии | Диэдрическая группа (D5) |
| Площадь | t 2 25 + 10 5 4 = <displaystyle <frac <sqrt <25+10<sqrt <5>>>>><4>>=> 5 R 2 4 5 + 5 2 ; <displaystyle <frac <5R^<2>><4>><sqrt <frac <5+<sqrt <5>>><2>>>;> 2> |
| Внутренний угол | 108° |
| Свойства | |
| выпуклый, вписанный, Равносторонний, равноугольный [en] , изотоксальный | |
| Медиафайлы на Викискладе | |
Правильный пятиугольник (или пентагон от греч. <circ >><2>>t=<frac <sqrt <5+2<sqrt <5>>>><2>>tapprox 1<,>539t>
<circ >><2>>t=<frac <sqrt <5+2<sqrt <5>>>><2>>tapprox 1<,>539t>
- Диагонали правильного пятиугольника являются трисектрисами его внутренних углов.
- Отношение диагонали правильного пятиугольника к стороне равно золотому сечению, то есть числу 1 + 5 2 <displaystyle <frac <1+<sqrt <5>>><2>>>.
Поэтому радиус вписанной окружности, радиус описанной окружности, высоту и площадь правильного пятиугольника можно вычислить и без использования тригонометрических функций:
R>
- Радиус вписанной окружности:
r = 5 5 + 2 5 10 t ≈ 0,688 191 t <displaystyle r=<frac <<sqrt <5>><sqrt <5+2<sqrt <5>>>>><10>>tapprox 0<,>688191
t>
- Радиус описанной окружности:
R = 1 0 5 + 5 10 t = ( 5 − 1 ) r ≈ 0,850 651 t ≈ 1,236 07 r <displaystyle R=<frac <<sqrt <1>>0<sqrt <5+<sqrt <5>>>>><10>>t=(<sqrt <5>>-1)
r>
- Диагональ:
d = Φ 5 R = 5 + 1 2 t ≈ 1,902 R ≈ 1,618 t <displaystyle d=<sqrt <Phi <sqrt <5>>>>R=<frac <<sqrt <5>>+1><2>>tapprox 1<,>902
t>
- Площадь:
S = 5 5 + 2 5 4 t 2 ≈ 1,720 48 t 2 <displaystyle S=<frac <<sqrt <5>><sqrt <5+2<sqrt <5>>>>><4>>t^<2>approx 1<,>72048
t^<2>>
- Правильным пятиугольником невозможно заполнить плоскость без промежутков (см.
 <4>=3Phi +2=<frac <3<sqrt <5>>+7><2>>approx 6<,>8541>где Φ <displaystyle Phi >— отношение золотого сечения.
<4>=3Phi +2=<frac <3<sqrt <5>>+7><2>>approx 6<,>8541>где Φ <displaystyle Phi >— отношение золотого сечения.Построение [ править | править код ]
Правильный пятиугольник может быть построен с помощью циркуля и линейки или вписыванием его в заданную окружность, или построением на основе заданной стороны. Этот процесс описан Евклидом в его «Началах» около 300 года до н. э.
Вот один из методов построения правильного пятиугольника в заданной окружности:
- Постройте окружность, в которую будет вписан пятиугольник, и обозначьте её центр как O. (Это зелёная окружность на схеме справа).
- Выберите на окружности точку A, которая будет одной из вершин пятиугольника. Постройте прямую через O и A.
- Постройте прямую перпендикулярно прямой OA, проходящую через точку O. Обозначьте одно её пересечение с окружностью как точку B.
- Постройте точку C посередине между O и B.

- Проведите окружность с центром в точке C через точку A. Обозначьте её пересечение с прямой OB (внутри первоначальной окружности) как точку D.
- Проведите окружность с центром в A через точку D, пересечение данной окружности с оригинальной (зелёной окружностью) обозначьте как точки E и F.
- Проведите окружность с центром в E через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку G.
- Проведите окружность с центром в F через точку A. Обозначьте её другое пересечение с первоначальной окружностью как точку H.
- Постройте правильный пятиугольник AEGHF.
Получение с помощью полоски бумаги [ править | править код ]
Правильный пятиугольник можно получить, завязав узлом полоску бумаги.
В природе [ править | править код ]
Исследования формирования водяного льда на ровной поверхности меди при температурах 100—140 K показали, что сначала на поверхности возникают цепочки молекул шириной около 1 нм не гексагональной, а пентагональной структуры.
 [1] Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как эта мушмула германская.
[1] Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как эта мушмула германская.Иглокожие, например морские звёзды, обладают пентасимметрией.
Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как мушмула германская.
Правильный пятиугольник представляет собой геометрическую фигуру, которая образовывается пересечением пяти прямых, создающих пять одинаковых углов. Такая фигура носит название — пентагон. С пятиугольником тесно связана работа художников — их рисунки строятся на основе правильных геометрических фигур. Для этого необходимо знать то, как быстро построить пентагон.
Чем интересна эта фигура? Форму пентагона имеет здание Министерства обороны Соединенных Штатов Америки. Это можно увидеть на фото, сделанных с высоты полета. В природе не существует кристаллов и камней, форма которых напоминала бы пентагон. Только в этой фигуре количество граней совпадает с числом диагоналей.

Параметры правильного пятиугольника
Прямоугольный пятиугольник, как и каждая фигура в геометрии, имеет свои параметры. Зная необходимые формулы, можно рассчитать эти параметры, что облегчит процесс построения пентагона. Способы и формулы расчетов:
- сумма всех углов в многоугольниках равна 360 градусам. В правильном пятиугольнике все углы равны, соответственно, центральный угол находится таким способом: 360/5 = 72 градуса;
- внутренний угол находится таким образом: 180*(n -2)/ n = 180*(5−2)/5 = 108 градусов. Сумма всех внутренних углов: 108*5 = 540 градусов.
Сторона пентагона находится с помощью параметров, которые уже даны в условии задачи:
- если вокруг пятиугольника описана окружность и известен ее радиус, сторона находится по такой формуле: a = 2*R*sin (α/2) = 2*R*sin (72/2) = 1,1756*R.
- Если известен радиус вписанной в пентагон окружности, то формула расчета стороны многоугольника: 2*r*tg (α/2) = 2*r*tg (α/2) = 1,453*r.

- При известной величине диагонали пентагона его сторона рассчитывается таким образом: а = D/1,618.
Площадь пентагона так же, как и его сторона, зависит от уже найденных параметров:
- с помощью известного радиуса вписанной окружности площадь находится так: S = (n*a*r)/2 = 2,5*a*r.
- описанная вокруг пятиугольника окружность позволяет найти площадь по такой формуле: S = (n*R2*sin α)/2 = 2,3776*R2.
- в зависимости от стороны пентагона: S = (5*a2*tg 54°)/4 = 1,7205* a2.
Построение пентагона
Построить правильный пятиугольник можно с помощью линейки и циркуля, на основе вписанной в него окружности или одной из сторон.
Как начертить пятиугольник на основе вписанной окружности? Для этого необходимо запастись циркулем и линейкой и сделать такие шаги:
- Сначала необходимо начертить окружность с центром О, после чего на ней выбрать точку, А — вершину пентагона. От центра к вершине проводится отрезок.

- Затем строится перпендикулярная прямой ОА отрезок, который также проходит через О — центр окружности. Его пересечение с окружностью обозначается точкой В. Отрезок О. В. делится пополам точкой С.
- Точка С станет центром новой окружности, проходящей через А. Точка D — это ее пересечение с прямой ОВ в границах первой фигуры.
- После этого проводится третья окружность через D, центром которой является точка А. Она пересекается с первой фигурой в двух точках, их необходимо обозначить буквами Е и F.
- Следующая окружность имеет центр в точке Е и проходит через А, а ее пересечение с первоначальной находится в новой точке G.
- Последняя окружность в этом рисунке проводится через точку, А с центром F. На ее пересечении с начальной ставится точка Н.
- На первой окружности после всех проделанных шагов появились пять точек, которые необходимо соединить отрезками. Таким образом получился правильный пятиугольник АЕ G Н F.
Как построить правильный пятиугольник иным способом? С помощью линейки и циркуля пентагон можно построить немного быстрее.

- Cначала необходимо с помощью циркуля нарисовать окружность, центр которой — точка О.
- Чертится радиус ОА — отрезок, который откладывается на окружность. Его делят пополам точкой В.
- Перпендикулярно радиусу ОА начерчивается отрезок ОС, точки В и С соединяются прямой.
- Следующим шагом является отложение длины отрезка ВС с помощью циркуля на диаметральной линии. Перпендикулярно отрезку ОА появляется точка D. Точки В и D соединяются, образуя новый отрезок.
- Для того, чтобы получить величину стороны пентагона, необходимо соединить точки С и D.
- D с помощью циркуля переносится на окружность и обозначается точкой Е. Соединив Е и С, можно получить первую сторону правильного пятиугольника. Следуя этой инструкции можно узнать о том, как быстро построить пятиугольник с равными сторонами, продолжая построение остальных его сторон подобно первой.
Интересные факты
В пятиугольнике с одинаковыми сторонами диагонали равны и образуют пятиконечную звезду, которая называется пентаграммой.
Золотое сечение — это отношение величины диагонали к стороне пентагона.
Пентагон непригоден для полного заполнения плоскости. Использование любого материала в этой форме оставляет промежутки или образует наложения. Хотя природных кристаллов этой формы не существует в природе, но при образовании льда на поверхности гладких медных изделий возникают молекулы в виде пентагона, которые соединены в цепочки.
Наиболее простой способ получить правильный пятиугольник из полоски бумаги — завязать ее узлом и немного придавить. Этот способ полезен для родителей детей-дошкольников, которые хотят научить своих малышей распознавать геометрические фигуры.
Видео
Посмотрите, как можно быстро начертить пятиугольник.
Здравствуйте коллеги.
Сегодня построим правильный пятиугольник в окружности, попробуем начертить циркулем и линейкой фигуру.Рисунки художников очень тесно связаны с черчением и геометрией. Если мы задумали какую-то композицию, а в ней есть геометрические фигуры, то нам необходимо знать, как изобразить предмет, что бы он не выглядел смешно, и что бы вы не выглядели дилетантом и смогли нарисовать пятиконечную звезду циркулем или в фотошопе.
 От этого зависит ваш авторитет художника, а значит и заказы.
От этого зависит ваш авторитет художника, а значит и заказы.Построение правильного пятиугольника не так часто встречается в рисунке, но все же есть моменты, когда нам это необходимо.
Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Это посмотрите в другом уроке.
Мы попробуем нарисовать звезду в фотошопе фронтально. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Всего лишь с помощью таких инструментов:
Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь. Количество углов не четное, поэтому просто разделить окружность на равные части циркулем или линейкой не получится.
Что бы вписанный пятиугольник в окружность был пропорциональный, нам необходимо точно вычислить одну из сторон, а затем отложить этот отрезок пять раз на теле овала.
Как выглядит пятиугольник и звезда
Внизу на фото разберем, как нарисовать звезду поэтапно.

Для начала рисуем окружность с центром О.Дальше отложим отрезок OA равный радиусу и разделим его пополам точкой B, как показано на фото внизу.
Теперь от точки В до точки С проведем прямую.Отложим расстояние отрезка ВС на диаметральной линии окружности. Для этого можно воспользоваться циркулем. Таким образом у нас появилась точка D.
И отрезок DB. Картинка внизу.Дальше, проведя линию от точки D к точке С, Мы получи длину равную стороне пятиугольника.
Дальше этот отрезок можно отложить на окружности. У нас появилась точка Е. Смотрим фото ниже.
Итак, одна из сторон пятиугольника у нас есть, это линия ЕС.Такие же отрезки наносим на всей части круга. Смотрим картинку.
На этом построение правильного пятиугольника можно закончить. Что бы нарисовать звезду нужно просто соединить углы через один.Нарисовать пятиконечную звезду циркулем можно так же, как и на нашем уроке в программе Photoshop, весь процесс такой же, только вместо программы графического редактора используем инструменты для черчения.

Так же можно посмотреть уроки построения шестиугольника, разделение на восемь частей, деление круга на семь частей, десять равных частей.
Многоугольники, виды многоугольников — ISaloni — студия интерьера, салон обоев
Содержание
стороны, вершины, диагонали. Периметр многоугольника
Многоугольник — это геометрическая фигура, ограниченная замкнутой ломаной линией, не имеющей самопересечений.
Звенья ломаной называются сторонами многоугольника, а её вершины — вершинами многоугольника.
Углами многоугольника называются внутренние углы, образованные соседними сторонами. Число углов многоугольника равно числу его вершин и сторон.
Многоугольникам даются названия по количеству сторон. Многоугольник с наименьшим количеством сторон называется треугольником, он имеет всего три стороны. Многоугольник с четырьмя сторонами называется четырёхугольником, с пятью — пятиугольником и т. д.

Обозначение многоугольника составляют из букв, стоящих при его вершинах, называя их по порядку (по часовой или против часовой стрелки). Например, говорят или пишут:
пятиугольник ABCDE
:В пятиугольнике
ABCDE точки A, B, C, D и E — это вершины пятиугольника, а отрезки AB, BC, CD, DE и EA — стороны пятиугольника.
Выпуклые и вогнутые
Многоугольник называется выпуклым, если ни одна из его сторон, продолженная до прямой линии, его не пересекает. В обратном случае многоугольник называется вогнутым:
Периметр
Сумма длин всех сторон многоугольника называется его периметром.
Периметр многоугольника ABCDE равен:
AB + BC + CD + DE + EA.
Если у многоугольника равны все стороны и все углы, то его называют правильным.
 Правильными многоугольниками могут быть только выпуклые многоугольники.
Правильными многоугольниками могут быть только выпуклые многоугольники.Диагональ
Диагональ многоугольника — это отрезок, соединяющий вершины двух углов, не имеющих общей стороны. Например, отрезок AD является диагональю:
Единственным многоугольником, который не имеет ни одной диагонали, является треугольник, так как в нём нет углов, не имеющих общих сторон.
Если из какой-нибудь вершины многоугольника провести все возможные диагонали, то они разделят многоугольник на треугольники:
Треугольников будет ровно на два меньше, чем сторон:
t = n — 2,
где t — это количество треугольников, а n — количество сторон.
Разделение многоугольника на треугольники с помощью диагоналей используется для нахождения площади многоугольника, так как чтобы найти площадь какого-нибудь многоугольника, нужно разбить его на треугольники, найти площадь этих треугольников и полученные результаты сложить
.

Polygon: от подвижных геометрических фигур до картин
Новости с курса Подвижная математика с Desmos: первые шаги.
В этом модуле мы учились воссоздавать с помощью несложного набора записей геометрические объекты, необходимые нам для визуализации задач по геометрии.
Но это совсем другие задачи — подвижной геометрии.
Причем, нам не нужна даже специальная среда desmos.geometry, знакомство с которой мы отложим до следующего нашего курса.
Здесь мы обойдемся одними аналитическими записями. Можно считать, что да, это аналитическая геометрия.
Несколько примеров того, как мы это делали:
Подвижные отрезки и ломаные
Подвижная ломаная https://www.desmos.com/calculator/18848b1dac
Подвижные многоугольники
1. Подвижный многоугольник с помощью таблицы
2. Подвижный закрашенный многоугольник с помощью таблицы и polygon(A,B,C,D,E)
Используя подвижные точки, отрезки, ломаные, многоугольники, можно создать интерактивные задания на множество математических тем:
от задач из «Математической шкатулки» до задач из школьного курса геометрии.

Вот здесь вы можете увидеть примеры таких задач, а ниже — ссылки на апплеты
Desmos-апплеты, использованные в активности
Модель картины с помощью команды polygon
С помощью подвижных многоугольников можно также моделировать картины, в которых много геометрических фигур.
Шаблон Картина Мондриана
Здесь, воспользовавшись образцом — картиной Мондриана, нужно сделать модель картины с помощью подвижных прямоугольников. Для этого ученику необходимо мысленно разметить имеющееся в распоряжении клетчатое пространство (справа). Линейные размеры не так важны, важнее пропорции и относительное расположении фигур. Отличительная черта этой учебной задачи в том, что нет никаких особенных инструкций по использованию инструментов: ученик должен сам для себя открыть возможность перемещать точки и менять положение и размеры объектов на клетчатой плоскости. В то же время, он имеет возможность самостоятельно проверять правильность своей модели, визуально сравнивая ее с образцом (слева).
 У ученика здесь есть та самая, упомянутая выше, возможность “возиться” с объектами.
У ученика здесь есть та самая, упомянутая выше, возможность “возиться” с объектами.Шаблон Sandor Bortnyik, Composition, 1922
Из картин подобных авторов «собирать» в desmos можно и более сложные в геометрическом плане картины. Например, эту. Заготовка
Предоставляю участникам возможность самим поискать подобные картины и создать шаблоны для их моделирования на основе предложенных прототипов.
Задачи от участников МК
Задачу на построение в интерактивной среде предложила Авраменко Владислава
https://www.desmos.com/calculator/u5ghtuswy3
Задачу на вычисление площади многоугольника с помощью вспомогательных линий предложила Юткина Наталья https://www.desmos.com/calculator/s7tiekyzqh
Ирина Кузнецова предложила задачу Участки https://www.desmos.com/calculator/0skab6jmfs
Вот одно из решений https://www.desmos.com/calculator/al5lrl3uta
Лехова Ирина придумала как визуализировать задачу Козы и капуста
https://www.
 desmos.com/calculator/ddakrfrdtl
desmos.com/calculator/ddakrfrdtlТатьяна Кротова предложила визуализацию знаменитой задачи Кобона
https://www.desmos.com/calculator/27qi8xh6pw
Игру Гонки https://www.
desmos.com/calculator/ufw2xikyhj создала Медведева Милана
Ждем новых идей и задач от участников!
Наш курс продолжается…
Публикации по теме
Многоугольные рамки для фото и картин
Многоугольные — в этой статье рассмотрим вопрос изготовления рамок, которые в некотором роде связаны с многоугольными формами. Лучше всего начать с того, что нужно вспомнить из далекой начальной школы, что такое многоугольник.
Многоугольные и математика для них
- Плоские замкнутые ломаные линии — общий случай;
- Плоские замкнутые ломаные линии без самопересечений — простые многоугольные;
- Часть плоскости, ограниченная замкнутыми ломаными линиями без самопересечений.
На рисунке ниже: (а) пятиугольник; (b) шестиугольник; (c) не является многоугольником, потому что он не замкнут; (d) не является многоугольником, потому что есть линии самопересечений; и (e) не является многоугольные, так как не все его линии являются прямыми.

Виды многоугольников, с разным числом ребер и их имена показаны на рисунке ниже.
Многоугольные формы
Обычные многоугольники имеют свойство, они находятся в кругу, который называется окружностью и соприкасается со всеми вершинами многоугольника. Центром правильного многоугольника всегда является центр его круга.
Допустим, что наш многоугольник имеет количество углов = N, круг имеет всегда 3600 и градус угла определяем из формулы 3600/N.
Например, шестиугольник имеет N=6 углов и образует угол в центре круга равный 3600/6 = 600.
Внутренние углы нашего многоугольника одинаковы и равны 1800( N-2 )/N градусов.
Например, внутренние углы квадрата равны 1800( 4-2 )/4 = 900; у восьмиугольника 1800( 8-2 )/8 = 1350.
По мере увеличения числа ребер в многоугольнике, длина ребра будет уменьшаться и в конечном итоге они сойдутся в одну окружность.

Некоторые изделия, имеющие многоугольную форму, без изменения размеров сторон показаны на рисунке ниже. Шкатулка имеет форму восьмиугольника, рамки для зеркала, которые имеют прямоугольную и шестиугольную формы. Разделочная доска, не правильный многоугольник, он состоит из двух форм, квадрата и восьмиугольника. Некоторые изделия, имеющие многоугольную форму, с изменением размеров сторон показаны на рисунке ниже. Ваза имеет семь сторон с наклоном в наружу, то есть снизу вверх, настольная лампа, наоборот, имеет наклон во внутрь с шестью сторонами.
Дальше рассмотрим ряд некоторых математических аспектов для многоугольников, которые нужны при расчете многоугольных изделий.Равносторонний многоугольник.
Главными переменными на многоугольные формы есть внутренние углы, длина ребер, и площадь изделия. Как видно из рисунка сегмент N-углов вписан в две окружности, обозначим их, как внутренний и внешний круг. Обозначим три стороны треугольника (стороны R, r, и l) его стороны образованы радиусами и ребром, обозначим три угла, которые расположены в треугольнике (А 1, А2 и А3).
 Между концами этих радиусов внутри двух кругов проведем линию с одной конечной точкой в месте касания к внутреннему кругу и другой точкой в месте касания к внешнему кругу. Радиус — отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка R. Радиус составляет половину диаметра 2R.
Между концами этих радиусов внутри двух кругов проведем линию с одной конечной точкой в месте касания к внутреннему кругу и другой точкой в месте касания к внешнему кругу. Радиус — отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка R. Радиус составляет половину диаметра 2R.Угол A1 составляет половину центрального угла и равен 1800/N для N-углов. Угол А2 = 900, потому что радиус круга (r) касается к сегменту (l) под прямым углом.
Это означает, что угол А3 и радиус (R) есть составляющие угла А1 и поэтому А3
=900-А1=900(N-2)/N. который является половиной внутреннего угла.
Две стороны определяют третью сторону треугольника, потому что R2=r2+l2. Определим стороны r и l по отношению к углу А1: r=Rcos А1 и l=Rsin А1.

Определим длину ребра L: L=2l=2Rsin А1, это формулы определения градусов в N-углах. [su_note note_color=»#c3f8a3″ radius=»6″].
Пример: Рассмотрим пятиугольник имеющий длину стороны L=1 дюйм. Угол А1=1800/5=360, угол А2=900-360=540.
Пятиугольник лежит внутри окружность радиуса R=L/(2sin А1)=1/(2sin 360)=0,85 дюйма.
Пример: Рассмотрим шестиугольник, внутренний круг, имеет диаметр 1,7 дюйма. Определяем радиус окружности R=1,7/2=0,85 дюйма. Угол А1=1800/6=300 и угол А3=600. Длина ребра равна L=2Rsin=1.7sin300=0,85 дюйма.[/su_note]
Углы А1 и А3 важны в создании формы правильного многоугольника и они отмечены в таблице для:
квадрата, пятиугольника, шестиугольника, восьмиугольника.
N углов центральный угол внутренний угол A1 A3 4 90 90 45 45 5 72 108 36 54 6 60 120 30 60 8 45 135 22,5 67,5 Разносторонние многоугольные.

Разносторонние многоугольники — те, которые имеют стороны не равной длины. Примеры угловых шкафов на рисунке ниже. Здесь углы и ребра разной длины и зависят от конкретных условий.
Те, кому интересна тригонометрия, формулы и примеры:
http://dls-website.com/documents/WoodworkingNotes/Compound%20Miters.pdf http://www.woodcentral.com/bparticles/miter_formula.shtml http://www.woodworkersguildofga.org/ShopHelpers/CompoundMiterTable.pdf Также существует программа написанная на языке Frink, которая позволяет делать расчеты для углов многоугольников на настольных компьютерах и смартфонах, Android-ах и iPhon-ах, она работает с компьютерами на платформе Андроид. Frink — компьютерный язык-программирования, на котором написана программа. Сама программа расположена по адресу: http://dls-website.com/documents/WoodworkingNotes/Compound%20Miters.pdf, там же описание программы и ее настройки. Инструкции по использованию языка-программирования можно получить бесплатно с сайтов: https://play.
 google.com/store/search?q=Frink+programming+language&c=apps и http://futureboy.us/frinkdocs/frinkframe.html . Один из способов реализовать использование языка-программирования Фринк, это загрузить его в настольный компьютер, который будет использоваться. После того как приложение заработает в среде рабочего стола, его можно будет отправить в сотовый телефон по проводному или беспроводному соединению. После загрузки в телефон, «приложение» может быть использовано там, как калькулятор. Онлайн калькуляторов расчета углов, для многоугольников,в интернете тоже предостаточно:
google.com/store/search?q=Frink+programming+language&c=apps и http://futureboy.us/frinkdocs/frinkframe.html . Один из способов реализовать использование языка-программирования Фринк, это загрузить его в настольный компьютер, который будет использоваться. После того как приложение заработает в среде рабочего стола, его можно будет отправить в сотовый телефон по проводному или беспроводному соединению. После загрузки в телефон, «приложение» может быть использовано там, как калькулятор. Онлайн калькуляторов расчета углов, для многоугольников,в интернете тоже предостаточно:
http://www.woodworkersguildofga.org/ShopHelpers/MiterCalculator.htm
http://jansson.us/jcompound.html
http://www.pdxtex.com/canoe/compound.htmТорцовочное приспособление на многоугольные. Торцовочное приспособление необходимо в различных проектах многоугольников, имеющих наклонные стороны. Ниже на рисунке показаны два необходимых реза под углом на циркулярном станке. Один из них создает углы торцов изделия, которые соединяют стороны многоугольника между собой, а другой рез создает углы наклона во внутрь или в наружу для каждой стороны, смотрите рисунок ниже.

Многогранники
Многоугольники являются двухмерными изделиями. Закрытые трехмерные изделия могут быть изготовлены из них путем присоединения многоугольников вдоль их краев. Объекты, полученные таким образом, называются многогранники. Куб полученный соединением шести квадратов является примером многогранника. Другим примером является додекаэдр, он показаны на рисунке слева и на рисунке ниже: (а) античная многогранная шкатулка; (б) додекаэдрическая система динамиков; (с) додекаэдрические солнечные часы, они построены из двенадцати одинаковых пятиугольников. Каждая пятиугольная грань составляет 0,5 дюйма толщиной красного дерева с использованием шаблона метод резки на рисунке ниже.
Важное значение в построении многогранников имеют скошенные уголки его многоугольных граней, детальнее: http://dls-website.com/documents/PolyhedralSundials.pdf
Любовные «многоугольники» Фрэнка Синатры — РИА Новости, 10.12.2010
И если бы не Ава Гарднер, то, возможно, на свет появился бы и еще один список фавориток.
 С Авой Фрэнк познакомился на съемках фильма «Джентльмены предпочитают блондинок». Молодая актриса не просто попала в список Синатры, она оказалась там единственной. Фрэнк настолько сильно увлекся Гарднер, что буквально вымаливал у своей супруги развод. После долгих уговоров Нэнси согласилась: Синатра и Гарднер обвенчались. Но…
С Авой Фрэнк познакомился на съемках фильма «Джентльмены предпочитают блондинок». Молодая актриса не просто попала в список Синатры, она оказалась там единственной. Фрэнк настолько сильно увлекся Гарднер, что буквально вымаливал у своей супруги развод. После долгих уговоров Нэнси согласилась: Синатра и Гарднер обвенчались. Но…И эта история завершилась размолвкой. В какой-то момент Ава стала успешнее своего возлюбленного. Разлад в отношениях стал наиболее явным, когда Фрэнк подарил Гарднер кольцо с бриллиантом, не сказав при этом, что купил его на деньги, снятые с ее кредитной карточки. «Я была замужем два раза, но никогда так долго», — иронизировала актриса на устроенной в эту честь вечеринке. Очередной удар по самолюбию Фрэнка, он уезжает на съемки фильма Ф. Циннемана «Отныне и во веки веков», где блестяще сыграл итальянца, солдата американской армии, забитого насмерть в тюрьме.
И вновь громкий успех, толпы поклонниц, мечтающих об одном — хотя бы на секунду оказаться в объятьях знаменитого сердцееда.
 Все это, безусловно, тешило самолюбие молодого артиста, он был невероятно заносчив, постоянно грубил, что жутко расстраивало Аву. В 1953 году их отношениям пришел конец. И для Синатры это обернулось настоящей трагедией.
Все это, безусловно, тешило самолюбие молодого артиста, он был невероятно заносчив, постоянно грубил, что жутко расстраивало Аву. В 1953 году их отношениям пришел конец. И для Синатры это обернулось настоящей трагедией.«Гангстер» 30-х
Синатру неоднократно обвиняли в связях с крупнейшими мафиози. Его приглашали участвовать в слетах и съездах международной мафии, он был тесно знаком с Джо Фишетти, племянником самого Аль Капоне.
«Тайм» писал о Синатре: «Мужчина, безусловно, внешне похож на общепринятый стандарт гангстера образца 1929 года. У него яркие, неистовые глаза, в его движениях угадываешь пружинящую сталь; он говорит сквозь зубы. Он одевается с супермодным блеском Джорджа Рафта — носит богатые темные рубашки и галстуки с белым рисунком… согласно последним данным, у него были запонки, примерно стоившие 30 000 долларов… Он терпеть не может фотографироваться или появляться на людях без шляпы или иного головного убора, скрывающего отступающую линию волос».

Тридцать девять лет — расцвет карьеры Фрэнка: награда академии за роль в картине «Отныне и вовеки веков», звание «первого великого певца спален наших дней». О себе в известном справочнике «Кто есть кто» он написал коротко и ясно — «баритон». Новая пассия — Лорен Бейколл, на которой он хотел жениться, но впоследствии передумал, ведь его ждала Мэрилин — Мэрилин Монро.
«Невинная» Монро
Виды многоугольников
Виды многоугольников:
Четырехугольники
Четырехугольники, соответственно, состоят из 4-х сторон и углов.
Стороны и углы, расположенные напротив друг друга, называются противоположными.
Диагонали делят выпуклые четырехугольники на треугольники (см. на рисунке).
Сумма углов выпуклого четырехугольника равна 360° (по формуле: (4-2)*180°).
Параллелограммы
Параллелограмм — это выпуклый четырехугольник с противоположными параллельными сторонами (на рис.
 под номером 1).
под номером 1).Противоположные стороны и углы в параллелограмме всегда равны.
А диагонали в точке пересечения делятся пополам.
Трапеции
Трапеция — это тоже четырехугольник, и в трапеции параллельны только две стороны, которые называются основаниями. Другие стороны — это боковые стороны.
Трапеция на рисунке под номером 2 и 7.
Как и в треугольнике:
— если боковые стороны равны, то трапеция — равнобедренная;
— если один из углов прямой, то трапеция — прямоугольная.
Средняя линия трапеции равна полусумме оснований и параллельна им.
Ромб
Ромб — это параллелограмм, у которого все стороны равны.
Помимо свойств параллелограмма, ромбы имеют своё особое свойство — диагонали ромба перпендикулярны друг другу и делят углы ромба пополам.
На рисунке ромб под номером 5.

Прямоугольники
Прямоугольник — это параллелограмм, у которого каждый угол прямой (см. на рис. под номером 8).
Помимо свойств параллелограмма, прямоугольники имеют своё особое свойство — диагонали прямоугольника равны.
Квадраты
Квадрат — это прямоугольник, у которого все стороны равны (№4).
Обладает свойствами прямоугольника и ромба (так как все стороны равны).
Редактировать этот урок и/или добавить задание Добавить свой урок и/или задание
Добавить интересную новость
Эффект боке в фотографии — Уроки фотографии
Наверняка вы слышали восхищенные возгласы типа «Ах, какое у него боке!» или «Мне так нравятся фотографии с боке!».
 Что означает это странное слово? И почему это боке в фотографии так всем нравится? Давайте разберемся вместе!
Что означает это странное слово? И почему это боке в фотографии так всем нравится? Давайте разберемся вместе!Слово «боке» (правильно произносить «бокЭ» с ударением на последний слог) пришло в русский язык от японского «??» (бокэ) «размытие, нечеткость». Боке в фотографии называют элемент изображения, которое оказалось вне зоны резкости. Именно характер размытия на фотографии зависит от формы и качества боке. Зачастую под боке понимают цветные пятна, которые получаются при размытии небольших световых пятен в зоне нерезкости (фонари, лучи света сквозь листву, вечерние окна домов и т.д.). И это не ошибка, потому что именно в этом случае можно детально разглядеть форму и характер боке.
На самом деле такими размытыми пятнами становятся все детали в зоне размытия на фотографии, и из таких маленьких «бокешек» складывается изображение в зоне нерезкости. Одно боке накладывается на другое, и мы получаем размытое изображение. Только вот разные объективы по-разному размывают фон.
 Это зависит от конструктивных особенностей конкретного объектива, которые влияют на форму боке. Посмотрим, какие виды боке встречаются и отчего это зависит.
Это зависит от конструктивных особенностей конкретного объектива, которые влияют на форму боке. Посмотрим, какие виды боке встречаются и отчего это зависит.Боке в видеIMG_7810-web[1] пятиугольников. Объектив Canon 50 mm 1.8, диафрагма 3.5, 5 лепестков диафрагмы
Форма боке в фотографии. Вы наверняка замечали, что на некоторых снимках световые пятна на заднем плане превращаются в размытые кружочки, а на других – в пяти-, шести- или восьмигранники. Дело в том, что форма боке зависит от строения диафрагмы объектива, а именно от количества лепестков. Чем больше лепестков, тем более округлым получается боке на фотографии. При меньшем количестве лепестков получаются многоугольники.
Практически идеально круглое боке. Объектив Canon 70-200 mm 4L, диафрагма 4, 8 лепестков диафрагмы
Более качественные и дорогие объективы обладают диафрагмой со множеством лепестков (8-10), что позволяет рисовать округлое боке.
 Традиционно считается, что идеальное боке с точки зрения художественности – это круглое пятно, которое дает объектив идеальной конструкции с максимально открытой диафрагмой. Однако интересного эффекта можно добиться и с объективами, которые рисуют боке в фотографии в виде многоугольника.
Традиционно считается, что идеальное боке с точки зрения художественности – это круглое пятно, которое дает объектив идеальной конструкции с максимально открытой диафрагмой. Однако интересного эффекта можно добиться и с объективами, которые рисуют боке в фотографии в виде многоугольника.На форму боке также влияет степень открытия диафрагмы. При полностью открытой диафрагме (f=1.2, 1.4, 1.8) лепестки разъезжаются до максимального значения, образуя максимально округлое отверстие. При закрытии диафрагмы лепестки сужаются, образуя тупые углы между каждым из элементов конструкции, и отверстие приобретает форму многоугольника с количеством углов, равным количеству лепестков. Также не забывайте, что чем сильнее закрыта диафрагма, тем меньше размытия на фотографии. Поэтому чтобы получить красивое боке в фотографии, сильнее открывайте диафрагму объектива.
Степень яркости боке в фотографии. Еще одна характеристика качества боке – это распределение яркости. В зависимости от этого выделяют три типа боке:
- Боке с высокой яркостью в центре и неяркими краями.
 Это мягкое боке, которое дает плавное и мягкое размытие. Множество размытых таким образом пятен накладываются друг на друга неяркими (размытыми) краями, и получается плавное размытие фона.
Это мягкое боке, которое дает плавное и мягкое размытие. Множество размытых таким образом пятен накладываются друг на друга неяркими (размытыми) краями, и получается плавное размытие фона. - Боке с низкой яркостью в центре и яркими краями (такие колечки или бублики). Это жесткое боке, которое приводит к не совсем красивому размытию. Порой такой тип боке дает задвоение контуров объектов в зоне нерезкости, что отвлекает внимание от главного объекта в кадре.
- Боке в равномерно распределенной яркостью. Это боке называют нейтральным, и оно может встретиться только у идеального объектива (с диафрагмой 1, то есть практически без диафрагмы в конструктивном смысле).
Как получить эффект боке на фотографии? Здесь под боке будем понимать именно размытые световые пятна, которые так нравятся многим ценителям фотографии. Такие пятна придают снимку атмосферность. Добиться эффекта боке достаточно просто: выберите объект съемки (человека или предмет), расположите его на фоне с множеством небольших источников света, которые могут превратиться в красивые цветные пятна.
 Теперь максимально открывайте диафрагму, фокусируйтесь на главном объекте и нажимайте кнопку спуска. Вуаля! Фотография с красивым боке у вас в портфолио!
Теперь максимально открывайте диафрагму, фокусируйтесь на главном объекте и нажимайте кнопку спуска. Вуаля! Фотография с красивым боке у вас в портфолио!Если не получается с первого раза подобрать правильную выдержку для нормальной экспозиции, прочитайте мою статью про экспозицию в фотографии тут.
Хороших вам снимков!
Как создать многоугольник в CorelDRAW
Инструмент Многоугольник на первый взгляд не создает впечатление креативного инструмента с широкими возможностями, ведь он предназначен для создания многосторонних многоугольников. Но этот урок убедит вас в обратном.
Как создать многоугольник в CorelDRAW
Для начала нам нужно начертить простой многоугольник. Для этого щелкните инструмент «Многоугольник» и протащите курсор в окне рисования, пока многоугольник не достигнет желаемых размеров.
Совет: для создания симметричного многоугольника (многоугольника с равными сторонами) удерживайте клавишу Ctrl, а для создания многоугольника от центра наружу — клавишу Shift.

После того, как многоугольник создан, выделите его с помощью инструмента Указатель. Количество сторон многоугольника может быть изменено в любой момент. Для этого в поле Точки или стороны на панели свойств нужно ввести число сторон. Помните, что для внесения изменений в объект его нужно выделить с помощью инструмента Указатель.
У нашего многоугольника 8 восемь сторон (восьмиугольник).
После того, как многоугольник создан, щелкните инструмент Форма и нарисуйте окно вокруг многоугольника.
Будут выделены два узла, а на панели свойств отобразятся параметры редактирования узлов. Нажмите значок Преобразовать в кривые.
На первый взгляд изменения не будут заметны. Однако, щелкнув один из узлов или путь многоугольника с помощью инструмента Форма и протащив курсор внутрь или наружу, вы заметите, что стороны многоугольника искривляются. Это позволяет создавать разнообразные формы.
 Посмотрите:
Посмотрите:
Вы можете продолжать изменять форму многоугольника. Для этого нужно щелкнуть и перетащить узлы и опорные маркеры.
Кроме того, к многоугольнику можно применить заливку цветом. Как видите, здесь я залила многоугольник черным цветом, щелкнув нужный образец цвета на цветовой палитре.
Замечательная особенность состоит в том, что в течение всего процесса исходный многоугольник можно модифицировать — изменять количество сторон многоугольника можно столько раз, сколько нужно.
Каждый раз при изменении количества сторон многоугольника будет создаваться новая фигура.
Попробуйте: выделите многоугольник и измените количество сторон. Для этого в поле Точки или стороны на панели свойств введите нужное число. Как и в этом примере, ваш многоугольник будет автоматически преобразован в новую форму.
Вы сможете взаимодействовать с каждым многоугольником в этом файле и убедиться в универсальности и огромных возможностях инструмента CorelDRAW Многоугольник.

Ссылка на источник
12 лучших низкополигональных генераторов для ярких фонов и изображений
Раскрытие информации: Ваша поддержка помогает поддерживать работу сайта! Мы зарабатываем реферальный сбор за некоторые услуги, которые мы рекомендуем на этой странице. Узнать больше
Поделиться — это забота!
Последнее обновление
Низкополигональные генераторы могут добавить интерес к вашим изображениям. А когда они используются в качестве фона, они помогают придать вашему сайту элегантный, но в то же время ретро-вид.
Этот стиль вошел в моду еще тогда, когда дизайнеры осознали, что могут использовать смелую и яркую геометрию для создания узоров или изображений, которые могут вызывать трехмерный вид.Но благодаря тому, насколько просты низкополигональные конструкции, они не требуют много места для хранения и пропускной способности.
Эта статья представляет собой введение в низкополигональные изображения, а также ссылки на лучшие бесплатные генераторы для создания с их помощью отличных фонов и других изображений.

Просто хотите приобрести один из низкополигональных генераторов? Переходите прямо к фоновым или специализированным генераторам!
История низкополигональных изображений
Низкополигональные изображения восходят к тому времени, когда началась компьютерная анимация.Многие из техник, используемых в этой форме анимации, восходят к началу 1940-х годов, когда в компьютерах даже не было экранов.
Спустя десятилетия компьютерная анимация стала мейнстримом и широко распространена.
К 1980-м годам трехмерные фигуры начали строиться с использованием полигональных сеток, что привело к появлению трехмерных видеоигр. В свою очередь, это привело к использованию компьютерной анимации и 3D-персонажей в таких фильмах, как Terminator 2 .
Изображение с сайта Pixabay
Низкополигональная игра использовалась в видеоиграх из-за быстрого рендеринга.Вы можете думать о лоу-поли как о особом виде мозаики, в которой используются многоугольные формы (треугольники, безусловно, являются наиболее распространенными).

Ключевыми примерами этого вида дизайна являются сетка треугольников, составляющих текстуры, типичные компьютерные фоновые изображения и даже целые изображения, в которых изображения имеют геометрические фигуры, соединенные друг с другом.
Низкополигональную мозаику можно рассматривать как особый вид мозаики, в которой используются многоугольные формы, причем треугольники являются наиболее распространенными.
При выполнении 3D-рендеринга дизайнеры достигают желаемого эффекта создания реалистичного персонажа, используя больше полигонов на изображении.
В веб-дизайне, однако, — полная противоположность . Количество используемых многоугольников сведено к абсолютному минимуму, поскольку основная идея здесь заключается в том, чтобы треугольные конструкции были четко видны.
Зачем нужны низкополигональные генераторы и искусство?
Дизайнеру часто приходится визуализировать трехмерное искусство, если он хочет отобразить такие качества, как освещение и анимация.
 Раньше для этого требовалось много вычислительной мощности и дорогих суперкомпьютеров.
Раньше для этого требовалось много вычислительной мощности и дорогих суперкомпьютеров.С годами дизайнеры узнали, что для уменьшения рабочей нагрузки и, следовательно, минимизации потребности в дорогостоящих суперкомпьютерах, достаточно , исключив количество полигонов в сетках.Это то, что мы сейчас называем «low poly».
Изображение через Pxhere
Несмотря на то, что сегодня вы можете купить ноутбук, достаточно мощный для рендеринга продвинутой компьютерной анимации, используя миллионы многоугольников на кадр, low poly по-прежнему процветает , потому что возвращает нас в более простые времена и Дизайнеры help создают более ретро-стиль.
Хотя вы всегда можете использовать фоторедакторы, такие как GIMP или Photoshop, для создания изображений для вашего веб-сайта, если вы хотите заполнить его геометрией, вы обычно будете использовать генераторы low poly или генераторы фона.

С учетом сказанного, вот список некоторых из лучших генераторов low poly на сегодняшний день.
Низкополигональные генераторы фона
Все следующие низкополигональные генераторы бесплатны. Если вам нужна еще большая мощность, у DMesh и HalftonePro есть недорогие премиум-версии.
1. Trianglify
Trianglify — это тот инструмент, который вам нужен, если вы хотите создавать низкополигональные фоны как можно быстрее…
Trianglify — это простое в использовании приложение, которое позволяет создавать низкополигональные фоны очень быстро. Небольшое время.Вы можете скачать их как файлы PNG.
Используемые цвета выбираются случайным образом и меняются со всеми новыми творениями. Вы можете легко контролировать размер и вариацию форм. Trianglify — это инструмент , который вам понадобится , если вы хотите как можно быстрее создавать низкополигональные фоны.
Trianglify предлагает на выбор 27 изысканных цветовых схем, которые надежны.
 Однако, если вам не нравится какой-либо из них, вы можете просто создать свою собственную цветовую схему с помощью 24-битной палитры цветов, предлагаемой в программе.
Однако, если вам не нравится какой-либо из них, вы можете просто создать свою собственную цветовую схему с помощью 24-битной палитры цветов, предлагаемой в программе.Снимок экрана с помощью Trianglify
2. DMesh
Гениальность DMesh заключается в том, что он может легко превращать уже существующие изображения в низкополигональные файлы, просто накладывая желаемую трехмерную треугольную сетку на двухмерное изображение.
DMesh на самом деле разработан для новичков…
Вы можете даже автоматически сгенерировать очки, но если вы хотите более изысканный вид, вам рекомендуется создавать свои собственные точки.
Хотя DMesh может выглядеть как продвинутый генератор фона или программа для редактирования изображений, на самом деле он разработан для новичков.Вот почему вы найдете такие полезные функции, как , автоматическое создание точек , что делает его очень простым в использовании.

Бесплатная версия DMesh не позволяет вам контролировать количество используемых полигонов или плотность распределения. Но с помощью ластика вы можете легко уменьшить количество треугольников, отображаемых в вашем изображении, после того, как это произошло.
С помощью DMesh вы можете экспортировать готовые файлы в форматы растрового изображения, Wavefront OBJ или PDF.
Снимок экрана через DMesh
3.HalftonePro
Это векторный генератор многоугольников с широким набором опций настройки, позволяющих создавать шестиугольные заголовки и кристаллические покрытия. Однако это не самый простой инструмент.
HalftonePro позволяет создавать детализированные градиенты с каждой настройкой, радикально меняющей изображение…
HalftonePro имеет широкий спектр сложных под поверхностью, что придает ему удивительные качества, которыми восхищается почти каждый дизайнер.

С помощью этого инструмента вы можете легко создавать детализированные градиенты с каждым параметром , радикально меняющим изображение и предоставляя вам больше возможностей обработки изображений.
Хотя это прекрасное дополнение, оно означает, что вы должны быть очень осторожны с количеством настроек, которые вы делаете, чтобы получить идеальный фон заголовка.
HalftonePro дает вам практически безграничные комбинации. Но он также предоставляет инструмент изменения размера, что означает, что вам не нужно использовать какие-либо другие редакторы изображений, если вы хотите уменьшить окончательное изображение до нужного размера.
Снимок экрана с помощью HalftonePro
4. Генератор треугольников Делоне
Прежде чем мы поговорим об этом низкополигональном генераторе, лучше всего объяснить «триангуляцию Делоне» в целом.
Генератор треугольников Делоне предоставляет вам до семи виртуальных источников света, которые значительно помогают, отбрасывая окружающий свет на холст…
Триангуляция Делоне — это математическая функция, которая определяет треугольник на основе массива точек.
 В этом дизайне ни одна из точек не находится внутри описанной окружности других треугольников. Это означает, что эта конструкция максимально избегает острых углов и в результате дает очень широкие и большие формы.
В этом дизайне ни одна из точек не находится внутри описанной окружности других треугольников. Это означает, что эта конструкция максимально избегает острых углов и в результате дает очень широкие и большие формы.Генератор треугольников Делоне основан на этих принципах. Инструмент дает вам до семи виртуальных источников света , которые очень помогают, отбрасывая окружающий свет на холст. Вы можете легко настроить цвета, а также их интенсивность.
Самое главное, однако, вы можете изменить количество полигонов, а также их мягкость.
Если вы хотите создать фон с великолепным люминесцентным узором и, как правило, элегантными изображениями, этот инструмент для вас.
Снимок экрана через MSurguy.github.io
5. Polyshaper
Polyshaper — простой в использовании, но мощный низкополигональный генератор…
Polyshaper — это веб-приложение, которое создает низкополигональное изображение на основе обычного изображения.
 Но это дает большой контроль.
Но это дает большой контроль.С Polyshaper вы можете вводить свои собственные баллы (но это не обязательно). А с помощью отдельных инструментов вы можете добавлять и удалять лишние треугольники.
Можно включать и выключать формы границ, а также заливку. Вы также можете изменить прозрачность этих элементов.
Кроме того, в Polyshaper есть инструментов для манипулирования цветом , которые позволяют получить ваше низкополигональное изображение именно таким, каким вы его хотите.
Снимок экрана с помощью Polyshaper
6.Генератор изображений триангуляции
Триангулятор — это очень простой в использовании низкополигональный генератор…
Генератор изображений триангуляции триангуляторов — очень простой в использовании инструмент. У него не так много вариантов, но он отлично подходит, если вам нужно низкополигональное изображение, но вас не слишком заботят его детали.

Как и многие генераторы low poly, Triangulator начинается с базового изображения и создает из него низкополигональное изображение. У него есть изображение по умолчанию, которое вы можете использовать.
Triangulator предлагает 3 алгоритма : Yape06 (с элементами управления Laplacian и Mineigen), Yape (с контролем радиуса) и Fast Corners (с контролем порогового значения). Yape06 обеспечивает максимальный контроль, а Fast Corners создает более типичные низкополигональные изображения.
Вы также можете установить любой размер изображения в соответствии с базовым изображением или 720p, 1080p и 2160p.
Снимок экрана через SnapBuilder
7. Генератор низкополигонального фона
С помощью низкополигонального генератора фона вы можете создать практически любой фон, который хотите…
Генератор низкополигонального фона прост в использовании.
 -используем еще и мощный .
-используем еще и мощный .Вы можете установить следующие значения:
- Размер изображения
- Вариант ячейки
- Размер ячейки
- Глубина ячейки
- Количество цветов
- Цвета
С помощью этих функций вы сможете создать почти любой фон по вашему желанию.
Снимок экрана через Codepen
Специализированные низкополигональные генераторы
Инструменты в этом разделе более специализированы, чем те, что указаны выше.Большинством из них интересно пользоваться. Но более того, они полезны блогерам для различных целей.
1. PolyGen
Это, безусловно, один из лучших низкополигональных генераторов, доступных для мобильных устройств (его можно найти как в App Store, так и в Play Store).
Безусловно, один из лучших низкополигональных генераторов, доступных для мобильных…
PolyGen действительно создан для личного использования, например для создания фоновых изображений и аватаров телефонов.
 Но он может быть полезен дизайнерам, которые в основном работают в дороге и на своих телефонах, чтобы создавать изображения, идеально подходящие для их мобильных проектов.
Но он может быть полезен дизайнерам, которые в основном работают в дороге и на своих телефонах, чтобы создавать изображения, идеально подходящие для их мобильных проектов.PolyGen, несомненно, невелик, но это не значит, что ему не хватает отличного контента. Он имеет список функций , который идет в ногу с любым полнофункциональным низкополигональным генератором для ПК, представленным сегодня на рынке. Кроме того, его можно использовать для создания красивых шаблонов дизайна или просто для упрощения изображений.
Можно было бы ожидать, что инструмента, который долгое время был монополистом на рынке мобильных низкополигональных генераторов, в некоторых областях будет немного не хватать. Будьте уверены, что это не относится к PolyGen.
Этот инструмент нисколько не жертвует качеством. Вот почему это инструмент для создания low-poly для мобильных пользователей и дизайнеров.
Снимок экрана через Google Play Store
2.
 I ♥ Δ
I ♥ ΔI ♥ Δ уникален для запуска в веб-браузере из кода на вашем локальном компьютере…
I ♥ Δ — это простой но забавный инструмент. Он позволяет импортировать растровую графику. Затем на основе этого изображения он создает поверх него слой, содержащий рандомизированные треугольники на основе изображения.
Можно объединить два изображения, изменив непрозрачность низкополигонального изображения. Однако, если вы хотите загрузить это изображение, вам нужно будет сделать снимок экрана. В противном случае вы можете сохранить только низкополигональное изображение в формате SVG или PNG.
I ♥ Δ уникален тем, что вы загружаете код на локальный компьютер, а затем запускаете его в веб-браузере. Это очень просто и быстро.
Снимок экрана через Игоря Борисенко
3. Триангуляция
Триангуляция позволяет легко преобразовать обычное изображение в низкополигональное…
Триангуляция — это веб-приложение, которое позволяет легко создавать низкополигональные изображения.
 поли изображения на основе изображения.Вы просто перетаскиваете изображение в него . Как только он появится, вы сможете контролировать количество точек, ширину обводки, размытие и точность.
поли изображения на основе изображения.Вы просто перетаскиваете изображение в него . Как только он появится, вы сможете контролировать количество точек, ширину обводки, размытие и точность.Триангуляция также имеет кнопку случайного выбора. Он рандомизирует четыре элемента управления, упомянутых выше. Это очень интересно, потому что это вырывает вас из ваших обычных склонностей и часто создает действительно необычные образы.
Помимо перетаскивания, изображения можно загружать или брать с веб-камеры. Вы также можете скачать изображение в формате PNG или SVG.И, наконец, вы можете поделиться им в Facebook, Twitter и Reddit.
Снимок экрана через snorpey.github.io
4. Poly Maker
Polymaker — это мощный инструмент, который не только интересен в использовании…
Poly Maker — удивительно мощный инструмент для тех, кто так много весело работать.

Это необычно во многих отношениях, но особенно с точки зрения того, что он использует для создания низкополигонального изображения: 4 выбранные пользователем точки, которые соответствуют кубической кривой Безье.Итак, вы запускаете любой проект, щелкнув 4 места на экране. Вы быстро узнаете, как эти точки определяют окончательное изображение.
Poly Maker имеет различные способы изменения изображения. Например, можно задать количество используемых шагов , а также двухцветную схему . Также есть много других настроек.
Вы также можете скачать изображения в формате PNG. При желании можно отобразить код SVG. Этот код можно скопировать и вставить в локальный файл.
Снимок экрана с помощью Aerotwist.com
5. Polygonize
Polygonize предоставляет простой способ сделать ваши изображения более интересными…
Polygonize — невероятно простой инструмент, но его можно использовать, чтобы оживить ваш блог .

Вы загружаете изображение (или вводите URL-адрес), а затем выбираете один из 15 фильтров Polygonize. Большинство фильтров представляют собой простые низкополигональные изображения, но некоторые сочетают их с другими графическими элементами.
Онлайн-версия ограничена изображениями размером 700 пикселей и менее.Если вам нужно более высокое разрешение, доступна недорогая версия для Windows.
Снимок экрана с помощью Polygonize
Как выбрать правильный низкополигональный генератор
Выбор правильного низкополигонального генератора действительно зависит от ваших общих дизайнерских навыков и того, чего вы хотите достичь в конечном итоге. Более продвинутые дизайнеры будут довольны очень сложными инструментами, такими как HalftonePro, в то время как те, кто только начинает, могут захотеть использовать DMesh или PolyGen.
Что вы хотите сделать, так это найти инструмент, обладающий следующими качествами:
- Простота использования
- Предоставляет вам больше всего вариантов, когда дело доходит до цветовой схемы
- Имеет большинство настроек, не будучи слишком сложными
- Позволяет вам для экспорта готовой работы в желаемый формат
- Имеет широкую сеть поддержки в Интернете
Любой из вышеупомянутых низкополигональных генераторов соответствует этим требованиям, но не так прост в использовании, и именно здесь проявляются ваш опыт и предпочтения играть.

Хотя всегда легче загружать готовые изображения, лучше использовать любой из этих низкополигональных генераторов для создания или изменения собственных, поскольку добавляет уникальный элемент на ваш веб-сайт .
Используйте любой из этих генераторов low poly, чтобы улучшить свой блог или другие проекты!
Фрэнк работает в Интернете с 1987 года. Когда блоги впервые появились, он отверг их как костыли, которыми пользуются люди, не умеющие программировать. Но в 2008 году он завел личный блог и влюбился.С тех пор он опубликовал около 10 000 сообщений в блогах.
Color by Polygon в App Store
Раскрашивайте по полигонам с помощью PolyColor! Поднимите раскраску на СЛЕДУЮЩИЙ БОЛЬШОЙ уровень! Создайте свои собственные художественные работы в стиле Low-Poly! Воображение запрещено!
Приготовьтесь к опыту Unique Polygon R T! Это НОВАЯ горячая тенденция в окрашивании, от которой невозможно отстать! Создайте свой собственный мозаичный шедевр из крошечных треугольников! Изображения превратились в причудливые геометрические произведения искусства!
Думаете, вы действительно не можете создавать картинки из тех, кто не из этого мира? Подумай еще раз! Никакого специального набора навыков не требуется! Выберите картинку, свяжитесь со своим внутренним художником и раскрасьте его по-своему с помощью потрясающего набора палитр и классных цветовых комбинаций! От яркого, энергичного, веселого до мрачного и драматичного! Придайте ему причудливую, футуристическую или просто настоящую цветовую атмосферу!
Используйте Poly Cam, чтобы сделать снимок, или выберите любое изображение, которое вам нравится, и превратите его в раскраску с геометрическим рисунком!
Если вы ищете расслабляющий и увлекательный способ развить свое творчество, вы его нашли! Простые геометрические фигуры расположены бок о бок! Отпустите свои заботы, расслабьтесь и погрузитесь в творческое настроение с PolyColor! Намного легче, чем вы думали!
ОСОБЕННОСТИ:
• Полигональное искусство! Мега потрясающий способ раскраски нового поколения!
• Сделайте потрясающие низкополигональные изображения!
• Сила идеального соответствия цветов! Стильная палитра для любых и всех картинок!
• Огромная коллекция картинок с угловатым рисунком! Скоро будут регулярные обновления!
• Используйте многоугольную камеру, чтобы сделать потрясающий снимок и превратить его в многоугольник!
• Супер-легкий антистресс! Не подчеркнул? Просто выпустите своего творческого зверя!
• Развлечения для всей семьи! И для взрослых, и для детей!
• Запишите процесс создания с помощью замедленных видеороликов!
• Удивите друзей и поделитесь своими шедеврами!
• Простой, чистый, минималистичный внешний вид!Не стесняйтесь написать нам: support @ exosmart.
 uk.com
uk.comПолучить PolyColor Premium
Подпишитесь на Premium, чтобы получить неограниченный доступ к полной коллекции полигональных изображений. Погрузитесь в мир современного футуристического искусства без ограничений!
-3 варианта подписки: еженедельная (7,99 долларов США, 3-дневная бесплатная пробная версия), ежемесячная (7,99 долларов США), годовая (39,99 долларов США).
-Подписавшись, вы получаете неограниченный доступ ко всем функциям приложения на весь период подписки.
— Оплата будет снята с учетной записи iTunes при подтверждении покупки.
-Подписка автоматически продлевается, если автоматическое продление не отключено по крайней мере за 24 часа до окончания текущего периода.
-Счет будет взиматься плата за продление в течение 24 часов до окончания текущего периода. «Бесплатная пробная версия»> 7,99 долл. США в неделю или продление соответствует выбранной первоначальной подписке и ее текущей цене, если не предлагается специальная цена.
-Вы можете отменить бесплатную пробную версию, управлять своей подпиской и отключить автоматическое продление в любое время через настройки своей учетной записи. Это необходимо сделать за 24 часа до окончания бесплатного пробного периода или периода подписки, чтобы избежать списания средств.
Это необходимо сделать за 24 часа до окончания бесплатного пробного периода или периода подписки, чтобы избежать списания средств.
-Политика конфиденциальности: http://exosmart.uk.com/index.php/privacy-policy/
-Условия использования: http://exosmart.uk.com/index.php/terms-of-use/
-Как только вы приобретете подписку, любая неиспользованная часть или период бесплатного пробного периода будет аннулирован.Создание многоугольника в App Store
PolyGen — приложение для низкополигонального искусства. Он позволяет создавать кристаллические узоры автоматически или вручную вручную.
Иногда в приложениях не так много возможностей для игры, что ограничивает ваше творчество.Из-за этого мы привыкаем выбирать предустановленные обои или использовать те же старые фильтры. Если бы только был инструмент, который позволил бы вам без особых усилий создавать красивые дизайны …
Откройте для себя PolyGen, приложение, которое позволяет каждому быть художником.

С помощью PolyGen вы можете:
— Создавать бесконечное количество полигонов
— Выбирать цвета, размеры, контраст и многое другое
— Создавать красивое абстрактное искусство
— И преобразовывать фотографии в геометрическое искусство
— Переключаться в редактор и размещать точки самостоятельно
— Используйте узор в качестве обоев вашего смартфона
— Или создайте аватары, фоны социальных сетей и многое другоеНекоторые из обзоров:
TUAW: PolyGen — это полезное приложение, которое позволяет вашему дому iOS и экранам блокировки выглядеть так, как вы может постоянно освежаться.
JC7133: Я давно искал подобное приложение. Количество настроек (огромное количество) настолько велико.
Cyberspace: нравится тот факт, что оно поддерживает размеры экрана рабочего стола. Больше не нужно искать в Интернете абстрактные обои!
PolyGen предлагает простые и полезные решения, заключенные в легкий в использовании интерфейс. Вы можете создавать новые полигональные узоры одним простым касанием.
 При желании вы можете контролировать процесс, а также легко «заблокировать» свои любимые атрибуты.Редактировать вершины фигур также просто: нажмите, чтобы создать одну, или нажмите на существующую, чтобы удалить ее.
При желании вы можете контролировать процесс, а также легко «заблокировать» свои любимые атрибуты.Редактировать вершины фигур также просто: нажмите, чтобы создать одну, или нажмите на существующую, чтобы удалить ее.Шаблоны PolyGen готовы к использованию в качестве обоев для мобильных устройств или рабочего стола, аватаров или фонов в социальных сетях. Пользователи поделились ими на арт-порталах и добавили в качестве иллюстраций в сообщения в блогах и социальных сетях. Узоры варьируются от красочных до спокойных, от простых до замысловатых, от абстрактных до фотореалистичных.
Какой узор вы собираетесь создать?
Посетите официальную галерею на Tumblr:
http: // PolyGenApp.tumblr.com/Как PolyGen на Facebook:
http://facebook.com/PolyGenAppПодпишитесь на PolyGen в Twitter:
http://twitter.com/PolyGenAppИнструмент «Многоугольное лассо» — выделение в Photoshop
По умолчанию инструмент «Многоугольное лассо» скрывается за стандартным инструментом «Лассо» на панели «Инструменты».
 Чтобы добраться до него, щелкните инструмент «Лассо», затем удерживайте кнопку мыши нажатой, пока не появится всплывающее меню с дополнительными доступными инструментами.Выберите инструмент Polygonal Lasso Tool из списка:
Чтобы добраться до него, щелкните инструмент «Лассо», затем удерживайте кнопку мыши нажатой, пока не появится всплывающее меню с дополнительными доступными инструментами.Выберите инструмент Polygonal Lasso Tool из списка:Инструмент «Многоугольное лассо» скрывается за стандартным инструментом «Лассо» на панели «Инструменты».
После того, как вы выбрали инструмент «Многоугольное лассо», он появится вместо стандартного инструмента «Лассо» на панели «Инструменты». Чтобы вернуться к инструменту «Лассо» позже, нажмите и удерживайте инструмент «Многоугольное лассо», затем выберите инструмент «Лассо» во всплывающем меню:
Какой из трех инструментов лассо, выбранных вами последним, появится на панели «Инструменты».Выберите остальные из раскрывающегося меню.
Вы можете циклически переключаться между тремя различными инструментами лассо в Photoshop (инструмент «Лассо», «Полигональное лассо» и «Магнитное лассо», которые мы рассмотрим позже), удерживая нажатой клавишу Shift и несколько раз нажимая букву L .

Плагин шорткодов, действий и фильтров: ошибка в шорткоде [ ads-basics-middle-2 ]
Рисование прямых многоугольных выделений
Рисование выделений с помощью инструмента «Многоугольное лассо» во многом похоже на рисование прямолинейных контуров с помощью инструмента «Перо» .Начните с щелчка где-нибудь вдоль края объекта или области, которую нужно выделить, затем отпустите кнопку мыши. Это добавляет к документу точку, обычно называемую точкой привязки или точкой крепления. Когда вы отодвинете инструмент «Многоугольное лассо» от точки, вы увидите тонкую прямую линию, выходящую из курсора мыши, немного похожую на паука, плетущего паутину, с другим концом линии, прикрепленным к точке привязки. Щелкните еще раз, чтобы добавить вторую точку, затем отпустите кнопку мыши. Линия будет «привязана» к новой точке, и теперь обе точки соединятся прямой линией.
Продолжайте перемещаться по объекту или области, щелкая, чтобы добавить новую точку в любом месте, где линия должна изменить направление, прикрепляя конец линии к каждой новой точке по мере продвижения.
 В отличие от стандартного инструмента «Лассо», а также многих других инструментов выделения Photoshop, нет необходимости удерживать кнопку мыши нажатой при перемещении от точки к точке. Просто щелкните, чтобы добавить точку, отпустите кнопку мыши, перейдите к следующему месту, где линия должна изменить направление, затем щелкните, чтобы добавить новую точку:
В отличие от стандартного инструмента «Лассо», а также многих других инструментов выделения Photoshop, нет необходимости удерживать кнопку мыши нажатой при перемещении от точки к точке. Просто щелкните, чтобы добавить точку, отпустите кнопку мыши, перейдите к следующему месту, где линия должна изменить направление, затем щелкните, чтобы добавить новую точку:Щелкните, чтобы добавить точки вокруг объекта или области, где необходимо изменить направление линии.
После того, как вы обошли объект или область, завершите выбор, еще раз щелкнув начальную точку, которую вы добавили. Photoshop преобразует все прямые линии в контур выделения. Когда вы достаточно приблизитесь к начальной точке, чтобы завершить выбор, в правом нижнем углу значка курсора появится маленький кружок. Я увеличил изображение, чтобы круг было легче рассмотреть:
Маленький кружок появляется в правом нижнем углу значка курсора, когда вы достаточно близко к начальной точке, чтобы завершить выбор.
Вы также можете закрыть выделение, просто дважды щелкнув в любом месте с помощью инструмента «Многоугольное лассо».
 Photoshop автоматически закроет выделение прямой линией от точки, на которой вы щелкнули, до начальной точки.
Photoshop автоматически закроет выделение прямой линией от точки, на которой вы щелкнули, до начальной точки.Вот фотография, которую я открыл в Photoshop, показывает большой пустой рекламный щит, висящий на стене здания. Я хочу добавить фотографию на рекламный щит, а это значит, что сначала мне нужно выбрать ее:
Пустой рекламный щит.
На первый взгляд может показаться, что рекламный щит имеет форму прямоугольника, так зачем использовать инструмент «Многоугольное лассо», если инструмент «Прямоугольная область» должен работать нормально? Давайте попробуем.Я нажимаю на клавиатуре букву M , чтобы быстро выбрать инструмент Rectangular Marquee Tool, затем щелкаю в верхнем левом углу рекламного щита, чтобы начать выделение, и перетаскиваю его в нижний правый угол. Чтобы завершить выбор, отпущу кнопку мыши:
Попытка выделить рекламный щит с помощью инструмента Rectangular Marquee Tool.
Как мы видим, даже если рекламный щит, вероятно, показался бы нам прямоугольным, если бы мы стояли прямо перед ним, угловая перспектива фотографии искажает его форму, и инструмент Rectangular Marquee Tool в конечном итоге выполняет довольно паршивую работу.
 выбирая это.
выбирая это.Я нажму Ctrl + D (Win) / Command + D (Mac), чтобы удалить мой неудачный контур выделения. На этот раз попробуем выбрать рекламный щит с помощью инструмента Polygonal Lasso Tool. Я возьму инструмент Polygonal Lasso Tool из панели инструментов, как мы видели ранее, затем, чтобы начать свой выбор, я щелкну в верхнем левом углу рекламного щита и отпущу кнопку мыши. Это устанавливает мою начальную отправную точку для выбора. Я перейду в верхний правый угол и нажму, чтобы добавить вторую точку.Photoshop соединяет две точки вместе тонкой прямой линией. Я нажимаю, чтобы добавить третью точку в правом нижнем углу, затем щелкаю, чтобы добавить четвертую точку в нижнем левом углу, прикрепляя прямую линию к каждой новой точке, когда я обхожу рекламный щит. Опять же, я не удерживаю кнопку мыши при перемещении от точки к точке. Я просто нажимаю, чтобы добавить точки, а затем каждый раз отпускаю кнопку мыши:
Щелкая в каждом из четырех углов с помощью инструмента «Многоугольное лассо», начиная с верхнего левого угла и двигаясь по часовой стрелке.

Если вы ошиблись и щелкнули, чтобы добавить точку не в том месте, нет необходимости начинать заново. Просто нажмите клавишу Backspace (Win) / Delete (Mac) на клавиатуре, чтобы отменить последнюю добавленную точку. Если вам нужно отменить несколько точек, продолжайте нажимать Backspace (Win) / Delete (Mac), чтобы отменить точки в обратном порядке, в котором они были добавлены.
Чтобы завершить свой выбор, я снова щелкну по начальной начальной точке для выбора в верхнем левом углу рекламного щита, затем отпущу кнопку мыши.Photoshop преобразует все прямые линии между точками в мой контур выделения, и, как мы видим, на этот раз мы смогли сделать гораздо лучшую работу по выбору рекламного щита:
Инструмент «Многоугольное лассо» упростил выбор билборда.
Теперь, когда рекламный щит выбран, я открываю изображение, которое хочу добавить к нему:
Фотография будущего билборда.
Я нажму Ctrl + A (Win) / Command + A (Mac), чтобы быстро выделить все изображение, затем Ctrl + C (Win) / Command + C (Mac) , чтобы скопировать его в буфер обмена.
 Чтобы добавить изображение на рекламный щит, я вернусь к своей исходной фотографии, затем перейду в меню Edit вверху экрана и выберу команду Paste Into :
Чтобы добавить изображение на рекламный щит, я вернусь к своей исходной фотографии, затем перейду в меню Edit вверху экрана и выберу команду Paste Into :Команда «Вставить в» в Photoshop позволяет нам вставлять изображение прямо в выделенную область.
Это помещает вторую фотографию прямо в выделенную область, и после небольшого изменения размера с помощью команды Photoshop Free Transform изображение появляется на рекламном щите для всеобщего обозрения:
Кому бы не понравилось быть больше, чем жизнь на рекламном щите?
Для более подробного объяснения того, как вставить одно изображение в другое, обязательно ознакомьтесь с нашим учебным курсом «Размещение изображения внутри другого изображения в Photoshop ».
Далее мы рассмотрим, как инструмент «Многоугольное лассо» справляется с чем-то более сложным, чем четырехсторонний рекламный щит, и что происходит, когда мы сталкиваемся с закругленной или изогнутой частью объекта!
Не все, что вы хотите выделить с помощью инструмента «Многоугольное лассо», будет таким же простым, как четырехсторонний рекламный щит, но шаги всегда одинаковы.
 Просто щелкните, чтобы добавить точки вдоль объекта в те места, где контур выделения должен изменить направление, затем щелкните обратно в начальной начальной точке, чтобы завершить выделение.
Просто щелкните, чтобы добавить точки вдоль объекта в те места, где контур выделения должен изменить направление, затем щелкните обратно в начальной начальной точке, чтобы завершить выделение.Вот фото старого здания. Я хочу заменить небо на фотографии, а это значит, что мне нужно выделить небо, нарисовав часть выделенной области вокруг верхней и боковых сторон здания. Поскольку здание почти полностью состоит из прямых плоских поверхностей, инструмент Polygonal Lasso Tool должен упростить задачу:
Чтобы выделить небо на фотографии, мне нужно выделить стороны и верх здания.
Я начну свой выбор где-нибудь с левой стороны здания, щелкнув мышью, чтобы задать начальную точку, затем я медленно пройду по внешней стороне здания, щелкая, чтобы добавить точки по мере необходимости.Я немного увеличу , чтобы было легче увидеть, что я делаю, нажав несколько раз Ctrl ++ (Win) / Command ++ (Mac). Чтобы прокрутить изображение внутри окна документа, нажмите и удерживайте пробел , который временно переключает вас на Ручной инструмент , затем щелкните и перетащите изображение, чтобы переместить его.
 Отпустите клавишу пробела, чтобы вернуться к инструменту «Многоугольное лассо»:
Отпустите клавишу пробела, чтобы вернуться к инструменту «Многоугольное лассо»: .
Лучше закройте окна. Инструмент «Многоугольное лассо» без труда поднимается по стенам зданий.
Переключение между инструментом «Многоугольное лассо» и стандартным инструментом «лассо»
Пробираясь по верху здания, я наткнулся на проблему. Часть конструкции на крыше на самом деле закруглена, что является плохой новостью для инструмента Polygonal Lasso Tool, поскольку он может рисовать только прямые выделения. К счастью, Photoshop позволяет легко переключаться между инструментом «Многоугольное лассо» и стандартным инструментом «лассо» в таких случаях, как этот. Просто удерживайте нажатой клавишу Alt (Win) / Option (Mac), затем начните перетаскивание с помощью мыши.Это временно переключает вас на стандартный инструмент Lasso Tool, и с его помощью мы можем легко обвести любые закругленные или изогнутые области объекта:
Удерживая Alt (Win) / Option (Mac), начните перетаскивание, чтобы временно переключиться на стандартный инструмент «Лассо».

Обведя край закругленной или изогнутой поверхности, отпустите клавишу Alt / Option, затем отпустите кнопку мыши. Вы снова переключитесь на инструмент Polygonal Lasso Tool, после чего вы можете продолжить движение вокруг объекта и щелкнуть, чтобы добавить больше точек:
Отпустите клавишу Alt (Win) / Option (Mac), затем отпустите кнопку мыши, чтобы вернуться к инструменту Polygonal Lasso Tool.
Как только я закончу рисовать выделение вокруг здания, я уберу все краевые пиксели неба по бокам и вверху фотографии, щелкнув инструментом «Многоугольное лассо» в серой области монтажного стола вокруг Фото. Если вы не видите область монтажного стола, нажмите несколько раз Ctrl + — (Win) / Command + — (Mac), чтобы уменьшить масштаб, пока не появится монтажный стол. Photoshop не выбирает монтажный стол, он выбирает только пиксели изображения:
Щелчок внутри области монтажного стола вокруг изображения — хороший способ убедиться, что вы выбрали все краевые пиксели.

Чтобы завершить выбор, я еще раз щелкну по исходной начальной точке, и теперь небо на фотографии выделено:
Небо готово к замене.
Я собираюсь вернуться к уровню масштабирования 100%, нажав Ctrl + Alt + 0 (Win) / Command + Option + 0 (Mac). Если мы посмотрим на мою панель «Слои», то увидим, что мой документ состоит из двух слоев. Фотография здания находится на верхнем слое, а фотография темного облачного неба находится на фоновом слое под ним:
Облака, которыми я хочу заменить небо, находятся на слое под изображением здания.
Выбрав верхний слой, я собираюсь удерживать клавишу Alt (Win) / Option (Mac) и щелкнуть значок Layer Mask в нижней части панели слоев. Это преобразует мой выбор в маску слоя , и мы видим, что миниатюра маски слоя была добавлена к верхнему слою. Обычно выбранный объект или область остаются видимыми в документе, в то время как все, что не было выделено, скрывается от просмотра, но, удерживая нажатой клавишу Alt / Option, я инвертировал маску слоя, которая скроет небо.
 (выбранная область) и оставить здание (невыделенную область) видимым:
(выбранная область) и оставить здание (невыделенную область) видимым:Черные области в маске слоя скрыты от просмотра в документе.Белые области остаются видимыми.
Когда небо на фотографии здания теперь скрыто, облака на фотографии ниже видны в документе:
Если вам не нравится погода в Photoshop, просто подождите несколько минут. Это изменится.
Удаление выделения
В приведенном выше примере контур выделения исчез, когда мы преобразовали его в маску слоя, но обычно, когда вы закончили с выделением, созданным с помощью инструмента Polygonal Lasso Tool, вы можете удалить его, перейдя в меню Select в верхней части экрана и выбрав Отменить выбор , или вы можете нажать сочетание клавиш Ctrl + D (Win) / Command + D (Mac).Вы также можете просто щелкнуть в любом месте документа с помощью инструмента «Многоугольное лассо» или любого другого инструмента выделения Photoshop.
Как использовать инструмент Photoshop «Многоугольник» для обновления портретов
Загрузите файлы проекта здесь
Дополнительные руководства по редактированию фотографий
Такие многоугольные портреты сейчас очень популярны, но прежде чем мы углубимся в это руководство, сначала предупреждаем: это займет некоторое время.

Нет волшебных фильтров, которые бы справились с этой задачей.Вместо этого каждая треугольная форма, которую вы видите на изображении, была терпеливо вычерчена вручную, поэтому для достижения приличного уровня детализации потребуется не менее часа или двух.
К счастью, после того, как начальные шаги выполнены и все настроено, построение треугольников — это тип повторяющейся работы, которую можно выполнять, слушая радио или даже наполовину смотря телевизор. Все эти усилия служат только для того, чтобы сделать конечный эффект более полезным.
Мы предоставили несколько начальных изображений, но гораздо лучше использовать один из ваших собственных снимков.Подойдет любой портрет, и это не обязательно должен быть человек — животные и домашние животные тоже подойдут.
Подробнее: Лучшие приложения для редактирования фотографий для устройств iOS и Android
Основная техника здесь очень проста. Сначала мы выбираем треугольную часть портрета.
 Затем мы применяем фильтр «Среднее», который показывает среднее значение для всех цветов в выделенной области, как если бы они смешивались в большом горшке. Затем мы просто повторяем этот процесс, пока он не закончится.
Затем мы применяем фильтр «Среднее», который показывает среднее значение для всех цветов в выделенной области, как если бы они смешивались в большом горшке. Затем мы просто повторяем этот процесс, пока он не закончится.К счастью, мы можем сэкономить время, просто записав быстрый экшен Photoshop, который сделает всю действительно тяжелую работу за нас. Мы даже можем назначить это действие сочетанию клавиш, так что единственное, что нам нужно сделать вручную, — это нарисовать каждый из треугольников.
• Получите больше идей фотосессии
Пошаговое руководство: приведите форму в Photoshop
Узнайте, как создать низкополигональный эффект, и узнайте, как действия могут значительно сэкономить время
1.Настройка и действие
Откройте изображение и на панели «Слои» нажмите «Новый слой». Выберите инструмент «Многоугольное лассо» и создайте случайный треугольник. Выберите «Окно»> «Действия», щелкните значок «Новый набор» и назовите его, затем щелкните значок «Новое действие».
 Назовите действие, назначьте функциональную клавишу и нажмите «Запись».
Назовите действие, назначьте функциональную клавишу и нажмите «Запись».2. Размытие до среднего
Точно соблюдайте этот бит. Щелкните слой «Фон», затем нажмите Ctrl + J, чтобы скопировать выделение на новый слой. Перейдите на панель «Слои» и, удерживая нажатой клавишу Ctrl, щелкните миниатюру слоя с треугольником, чтобы загрузить фигуру в качестве выделения.Перейдите в Фильтр> Размытие> Среднее, затем нажмите Ctrl + D, чтобы снять выделение.
3. Сделайте края более четкими
Нажмите кнопку «Fx» на панели «Слои» и выберите «Обводка». Установите Размер: 1, Положение: Внутри, Режим наложения: Разница, Непрозрачность: 100% и установите белый цвет, чтобы края были более четкими. Нажмите «ОК», затем нажмите «Остановить» на панели «Действия». Перетащите два верхних слоя в корзину.
БЫСТРЫЙ СОВЕТ!
Используя инструмент «Многоугольное лассо», дважды щелкните, чтобы отправить выделение обратно в начальную точку.
 Backspace удаляет предыдущую точку.
Backspace удаляет предыдущую точку.4. Включите сетку
Перейдите в «Настройки» и щелкните «Направляющие, сетки и фрагменты». Установите подходящий размер сетки, например 5 пикселей. Перейдите в меню «Просмотр»> «Показать»> «Сетка», затем «Просмотр»> «Привязать к» и установите флажок «Сетка». Сделайте треугольное выделение с помощью Polygonal Lasso — оно должно привязаться к сетке. Нажмите сочетание клавиш «Действие».
5. Заполните портрет
Выберите треугольник, запустите действие и повторяйте, пока не закончите.Попробуйте разделить лицо на разные по тональности и детализации участки. Каждый треугольник должен встречаться в угловых точках соседнего, чтобы стороны совпадали. Используйте треугольники меньшего размера в деталях, например, в глазах.
6. Настройте стили
Дважды щелкните Стиль обводки. Установите режим наложения: Умножение, Непрозрачность: 10%. Нажмите «Наложение градиента», выберите «От черного к белому», режим наложения: мягкий свет, непрозрачность: 20%.
 Щелкните правой кнопкой мыши> Копировать стиль слоя, щелкните верхний и нижний треугольные слои, удерживая клавишу Shift, щелкните правой кнопкой мыши> Вставить стиль слоя.
Щелкните правой кнопкой мыши> Копировать стиль слоя, щелкните верхний и нижний треугольные слои, удерживая клавишу Shift, щелкните правой кнопкой мыши> Вставить стиль слоя.Как правильно
Чтобы низкополигональный эффект выглядел правильно, каждую форму треугольника нужно аккуратно стыковать с соседней, а точки выровнять так, чтобы ни один треугольник не пересекал стороны другого. Мы также должны убедиться, что все аккуратно соединено. Вот почему мы включаем «привязку к сетке», чтобы точки сетки становились немного липкими. По-прежнему требуется много терпения, чтобы точно нанести каждую точку (особенно на таком портрете, который состоит из более тысячи слоев).После завершения изучите изображение, и если вы заметите какие-либо пробелы, удалите слой и повторите выделение.
Подробнее: Как удалить и заменить небо в Photoshop
Эволюция изображения
Что это?
Имитация отжига, подобная алгоритму оптимизации, повторная реализация Отличная идея Роджера Алсинга.
 Цель состоит в том, чтобы получить изображение , представленное как набор перекрывающихся многоугольников различных цветов и прозрачностей .
Цель состоит в том, чтобы получить изображение , представленное как набор перекрывающихся многоугольников различных цветов и прозрачностей .Мы начинаем со случайных 50 невидимых полигонов. На каждом шаге оптимизации мы случайным образом изменяем один параметр (например, компоненты цвета или вершины многоугольника) и проверьте, больше ли такой новый вариант похож на исходное изображение. Если это так, мы сохраняем его и продолжаем видоизменять его.
Фитнес — это сумма попиксельных отличий от исходного изображения. Чем меньше число, тем лучше.
Отображаемая пригодность теперь выражается в процентах от того, насколько близко новое изображение к исходному (1-текущая разница / максимальная разница).Лучшее из возможных — 100%. Эта новая приспособленность нормализована, чтобы было легче сравнивать разные изображения и разные размеры.Эта реализация основана на описании Роджера Алсинга, но не на его коде. Вероятно, есть некоторые тонкие различия в том, как выполняются мутации, как представлены полигоны и как вычисляется приспособленность, когда я пытался выяснить, как пусть он работает достаточно быстро в среде JavaScript +
Как это выглядит через некоторое время?
- 50 полигонов (4 вершины)
- ~ 15 минут
- 644 полезные мутации
- 6120 кандидатов
- 88.
 74% фитнес
74% фитнес
- 50 полигонов (6 вершин)
- ~ 15 минут
- 646 полезных мутаций
- 6024 кандидата
- 89,04% пригодность
- 50 полигонов (10 вершин)
- ~ 15 минут
- 645 полезных мутаций
- 5367 кандидатов
- 87,01% пригодность
- 50 полигонов (6 вершин)
- ~ 45 минут
- 1476 полезных мутаций
- 23694 кандидата
- 93.35% фитнес
- 50 полигонов (6 вершин)
- ~ 60 минут
- 1595 полезных мутаций
- 28 888 кандидатов
- 93,46% фитнес
- 50 полигонов (6 вершин)
- ~ 120 минут
- 1966 полезных мутаций
- 50 500 кандидатов
- 93.89% фитнес
- 50 полигонов (6 вершин)
- ~ 4 часа
- 4134 полезные мутации
- 807 890 кандидатов
- 95,59% фитнес
- Спасибо Сергею.
- 50 полигонов (6 вершин)
- ~ 2 дня
- 7 425 полезных мутаций
- 5 288 801 кандидат
- 96.
 36% фитнес
36% фитнес - Спасибо Джулиану.
- 1000 полигонов (12 вершин)
- ~ 7 дней
- 21135 полезных мутаций
- 8 143 969 кандидатов
- 97,12% пригодность
- Спасибо Богдану.
На всех образах работает?
Это зависит от успеха. Лучше всего выглядят цветные изображения с четко определенными характеристиками.
- 50 полигонов (6 вершин)
- 4358 полезных мутаций
- 227 852 кандидата
- 95,97% фитнес
- Спасибо Quialiss.
- Изображения из разных прогонов.
- 50 полигонов (6 вершин)
- 718+ полезных мутаций
- 22 440+ кандидатов
- 95.24% фитнес
- Изображения из разных прогонов.
- 100 полигонов (6 вершин)
- 9686 полезных мутаций
- 1,220,569 кандидатов
- 96,21% фитнес
- Спасибо Стивену.

- 100 полигонов (5 вершин)
- 10490 полезных мутаций
- 2 161 018 кандидатов
- 95.03% фитнес
- Спасибо Асе, Уиллу, Нику и Юку.
- Изображения из разных прогонов.
- 50 полигонов (6 вершин)
- 6280 полезных мутаций
- 683 806 кандидатов
- Спасибо alexs за финальное изображение.
- Изображения из разных прогонов.
- 100 полигонов (5 вершин)
- 6974 полезные мутации
- 2,056,467 кандидатов
- 95.68% фитнес
- Спасибо Юку.
- 100 полигонов (6 вершин)
- 6,557 полезных мутаций
- 44 212 346 кандидатов
- 99,43% пригодность
- Спасибо Алексу.
- 50 полигонов (5 вершин)
- 8031 полезная мутация
- 1,099,366 кандидатов
- 96.
 14% фитнес
14% фитнес - Спасибо Karol Masztalerz.
- 50 полигонов (6 вершин)
- 4296 полезных мутаций
- 2404942 кандидата
- 97,6% фитнес
- Спасибо Кайлу.
- 50 полигонов (6 вершин)
- 10605 полезных мутаций
- 11 104 153 кандидата
- 93.84% фитнес
- Спасибо KRHAiNOS.
- 50 полигонов (6 вершин)
- 11147 полезных мутаций
- 1,021,165 кандидатов
- 95,04% пригодность
- Спасибо Саймону.
См. Также видео об эволюции логотипа Firefox. Спасибо Brooss.
- Объем распределенных вычислений: исходный размер изображения 600 пикселей X 900 пикселей, разделенных на 24 части, каждая по 150 X 150 пикселей
- 24 x 100 полигонов (6 вершин)
- 109 438+ полезных мутаций (всего)
- 8243441+ кандидатов (всего)
- Фитнес: мин.
 95.01%, макс 99,08%, среднее 96,59%, медиана 96,65%
95.01%, макс 99,08%, среднее 96,59%, медиана 96,65% - Спасибо Agro momusuindo.net (Индонезия).
- Окончательное изображение с полным разрешением
- 6278 полезных мутаций
- 267 623 кандидата
- 96,95% фитнес
- 4208 полезных мутаций
- 8 451 873 кандидата
- 97.88% фитнес
- 6250 полезных мутаций
- 10418975 кандидатов
- 98,38% пригодность
- 6281 полезная мутация
- 226 689 кандидатов
- 96,75% фитнес
- Спасибо Маринке за персонажей Южного парка.
- 100 полигонов (5 вершин)
- 7310 полезных мутаций
- 5 430 510 кандидатов
- 96.53% фитнес
- Спасибо Магнусу Хансену.
- 95,79% пригодность
- 1 день 9 часов
- Спасибо Кристиану Гроссеру.
Что такое импорт / экспорт ДНК?
Предупреждение: еще одна экспериментальная (которая вообще не тестировалась) функция.
 Большинство ошибок должны быть исправлены сейчас.
Большинство ошибок должны быть исправлены сейчас.Нажмите Экспорт ДНК , чтобы скопировать полигональное представление текущего лучшего изображения в буфер обмена.Вы можете использовать его для сохранения состояния оптимизации, например, чтобы отправить его кому-нибудь по почте или разместить в сети.
Если у вас есть такая сохраненная строка ДНК, вы можете позже вставить ее в буфер обмена и нажать Импортировать ДНК . Это должно воспроизвести состояние оптимизации с момента сохранения через экспорт.
Обратите внимание, что ДНК не зависит от исходного изображения. Это означает, что если вы использовали собственное изображение, вы также должны настроить это изображение (через форму изображения) для воспроизведения полное состояние.(Или вы можете поиграть с переключением изображений / ДНК на полпути)
Формат ДНК очень простой (все числа — INT, кроме ALPHA, которая имеет FLOAT):
ЧИСЛО_OF_VERTICES NUMBER_OF_POLYGONS R G B АЛЬФА X0 Y0 X1 Y1 .
 .. XN YN ... R G B АЛЬФА X0 Y0 X1 Y1 ... XN YN ...
.. XN YN ... R G B АЛЬФА X0 Y0 X1 Y1 ... XN YN ... Нажмите Экспортировать ДНК как SVG , чтобы получить векторное изображение из вашей лучшей на данный момент ДНК. Спасибо Мартину за экспорт SVG.
Требования
Протестировано и работает (пример скорости мутации для Моны Лизы в начале оптимизации на моем ноутбуке):
- Firefox 29 (~ 222 мутации в секунду)
- Хром 34 (~ 209 мутаций в секунду)
- Explorer 11 (~ 182 мутации в секунду)
Не стесняйтесь улучшать мою реализацию.Код довольно уродливый, хотя и некрасивый по соображениям производительности.
Фотоскан — Редактирование ортофотоплана — GeoCue Group
Photoscan имеет функцию назначения только выбранных пользователем изображений для определенной области. Это полезно для очистки областей ортофокуса, которые имеют: размытость, движущиеся транспортные средства, плохое сшивание изображений и т. Д. Созданные полигоны также могут использоваться для определения подмножества области проекта для экспорта.

Монтаж
1.Для начала убедитесь, что вы выбрали просмотр ортофотоплана, нарисуйте многоугольник вокруг области ортофотоплана, в которой есть проблемы. Используйте инструмент Draw Polygon , который находится на панели инструментов. Щелкните левой кнопкой мыши по области, которую необходимо отредактировать, и дважды щелкните, чтобы закончить. (Рисунок 1)
фигура 1
2. Щелкните правой кнопкой мыши многоугольник и выберите Назначить изображения. (рисунок 2)
фигура 2
3. Что касается заменяющих изображений для выбранной области, можно назначить одну фотографию или несколько фотографий.Когда вы щелкаете по доступным фотографиям в окне «Назначить изображения», изображения изменяются в области многоугольника. Выберите фотографии, которые изменяют область до желаемого вида. Когда вы закончите, нажмите ОК. (Рисунок 3)
Рисунок 3
4.
 Чтобы применить изменения, которые вы выбрали для ортофотоплана: вы должны обновить ортофотоплан после назначения изображений в выбранной области. Нажмите кнопку Обновить ортофотоплан . Эта кнопка будет выделена только после того, как вы назначили изображения.(Рисунок 4)
Чтобы применить изменения, которые вы выбрали для ортофотоплана: вы должны обновить ортофотоплан после назначения изображений в выбранной области. Нажмите кнопку Обновить ортофотоплан . Эта кнопка будет выделена только после того, как вы назначили изображения.(Рисунок 4)Рисунок 4
5. После нажатия этой кнопки и принятия изменений она снова станет серой. Теперь ортомозиум должен отражать изменения, которые вы выбрали в окне ортофотоплана Photoscan и экспортировать.
Определение области проекта
1. Для начала нарисуйте многоугольник вокруг области, которая будет использоваться в качестве границ для экспорта ортофотоплана. Используйте инструмент «Нарисовать многоугольник», расположенный на панели инструментов.
Семиугольник, виды, свойства и формулы — ISaloni — студия интерьера, салон обоев
Содержание
Семиугольник, виды, свойства и формулы
Семиугольник, виды, свойства и формулы.

Семиугольник – это многоугольник, общее количество углов (вершин) которого равно семи.
Семиугольник, выпуклый и невыпуклый семиугольник
Правильный семиугольник (понятие и определение)
Свойства правильного семиугольника
Формулы правильного семиугольника
Семиугольник в природе, технике и культуре
Шестиугольник, семиугольник, восьмиугольник
Семиугольник, выпуклый и невыпуклый семиугольник:
Семиугольник – это многоугольник с семью углами.
Семиугольник – это многоугольник, общее количество углов (вершин) которого равно семи.
Семиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.
Соответственно выпуклый семиугольник – это семиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Звёздчатый семиугольник – семиугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного семиугольника многоугольника. Стороны звёздчатого семиугольника могут пересекаться между собой.
Рис. 1. Выпуклый семиугольник
Рис. 2. Невыпуклый семиугольник
Сумма внутренних углов любого выпуклого семиугольника равна 900°.
Правильный семиугольник (понятие и определение):
Правильный семиугольник – это правильный многоугольник с семью сторонами.
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
Правильный семиугольник – это семиугольник, у которого все стороны равны, а все внутренние углы равны 128 4/7° ≈
128,571°.
Рис. 3. Правильный семиугольник
Правильный семиугольник имеет 7 сторон, 7 углов и 7 вершин.

Углы правильного семиугольника образуют семь равнобедренных треугольников.
Правильный семиугольник можно невозможно построить с помощью циркуля и линейки, но можно построить с помощью циркуля и невсиса, то есть размеченной линейки, на которой можно делать отметки и с помощью которой можно проводить прямые, проходящие через какую-нибудь точку, причём отмеченные на линейке точки будут принадлежать данным линиям (прямым или окружностям).
Свойства правильного семиугольника:
1. Все стороны правильного семиугольника равны между собой.
a1 = a2 = a3 = a4= a5 = a6 = a
7. 2. Все углы равны между собой и составляют 128 4/7° ≈ 128,571°.
α1 = α2 = α3 = α4 = α5 = α6 = α7 = 128 4/7° ≈ 128,571°.

Рис. 4. Правильный семиугольник
3. Сумма внутренних углов любого правильного семиугольника равна 900°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного семиугольника O.
Рис. 5. Правильный семиугольник
5. Количество диагоналей правильного семиугольника равно 14.
Рис. 6. Правильный семиугольник
6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.
Рис. 7. Правильный семиугольник
Формулы правильного семиугольника:
Пусть a – сторона семиугольника, r – радиус окружности, вписанной в семиугольник, R – радиус описанной окружности семиугольника, P – периметр семиугольника, S – площадь семиугольника.
Формулы стороны правильного семиугольника:
Формулы периметра правильного семиугольника:
Формулы площади правильного семиугольника:
Формулы радиуса окружности, вписанной в правильный семиугольник:
Семиугольник в природе, технике и культуре:
В некоторых странах, например, в Великобритании, некоторые монеты имеют правильную криволинейную семиугольную форму.

Некоторые виды кактусовых имеют форму звездчатого семиугольника.
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Шестиугольник
Восьмиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
карта сайта
Коэффициент востребованности 773
Онлайн калькулятор: Площадь многоугольника
Пример многоугольника
Данный калькулятор обсчитывает площадь многоугольника по введенным сторонами и диагоналям, разбивающим многоугольник на непересекающиеся треугольники.
Смотрим на картинку — площадь многоугольника ABCDE можно вычислить как сумму площадей треугольников ABD, BCD и ADE. Для этого, понятно, помимо длин сторон многоугольника, надо знать еще и длины диагоналей BD и AD, но это и все что нужно — площадь любого треугольника можно вычислить только по длинам его сторон, без измерения углов.

А это довольно удобно, например, при бытовом ремонте — длины-то всяко проще померять, чем углы.
Итак, измеряем длины сторон интересующего нас многоугольника, заносим их в таблицу, мысленно разбиваем многоугольник на треугольники, измеряем нужные диагонали, также заносим их в таблицу, после чего калькулятор рассчитывает площадь всей фигуры. Для проверки также выводятся площади обсчитанных им треугольников. В поле «Ошибка» выводится вершина, которую не удалось сопоставить ни одному треугольнику (если, например, введены еще не все диагонали).
По умолчанию в таблицу введены стороны и диагонали многоугольника на картинке, что легко исправить, нажав кнопку «Очистить таблицу».
Площадь многоугольника
addimport_exportmode_editdelete
Стороны и диагонали
Размер страницы: chevron_leftchevron_right
Стороны и диагонали
Сохранить Отменить
Импортировать данныеОшибка импорта
Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: ? EFGHIJKLMNOPQRSTUVWXYZ ?;50.
 5
5Загрузить данные из csv файла
Импортировать Назад Отменить Точность вычисления
Знаков после запятой: 2
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Загрузить close
content_copy Ссылка save Сохранить extension Виджет
Выпуклый, невыпуклый и звездчатый многоугольник
Плоская фигура, образованная замкнутым рядом прямолинейных отрезков, называется многоугольником. На рис.1 изображен шестиугольник ABCDEF. Точки А, В, С, D, Е, F — вершины многоугольника; углы при них (углы многоугольника) обозначаются ∠A, ∠В, ∠С, …, ∠F. Отрезки: AC, AD, BE и т.д. — диагонали, АВ; ВС, CD и т. д. — стороны многоугольника
; сумма длин сторон АВ + ВС + CD + … + FA называется периметром и обозначается р, а иногда 2р (тогда р — полупериметр).

рис.1
В элементарной геометрии рассматриваются только простые многоугольники, т. е. такие, контур которых не имеет самопересечений.
Многоугольники, контур которых имеет самопересечения, называются звездчатыми многоугольниками. На рис.2 изображен звездчатый многоугольник ABCDE.
рис.2
Если все диагонали многоугольника лежат внутри него, многоугольник называется выпуклым.
Шестиугольник на рис.1 выпуклый; пятиугольник на рис.3 невыпуклый (диагональ ЕС лежит вне многоугольника).
рис.3
Сумма внутренних углов во всяком выпуклом многоугольнике равна 180° (n-2), где n — число сторон многоугольника*.
* В учебниках геометрии это свойство высказывается обычно только для выпуклых многоугольников. Но оно справедливо для всех простых многоугольников. Но оно справедливо для всех простых многоугольников. Нужно заметить, что в невыпуклом многоугольнике один или несколько внутренних углов превышают 180°.
 Так, в невыпуклом пятиугольнике, изображенном на рис.3, два угла прямые, два угла имеют по 45°, а один содержит 270°. Суммаа углов составляет 180° (5-2)=540°.
Так, в невыпуклом пятиугольнике, изображенном на рис.3, два угла прямые, два угла имеют по 45°, а один содержит 270°. Суммаа углов составляет 180° (5-2)=540°. Как обрезать фотографии под разными углами — Вокруг-Дом
Типичный инструмент обрезки позволяет обрезать фотографию в квадратную или прямоугольную форму. Но иногда желательно подрезать под разными углами. Используйте инструменты маскировки и выделения для этого типа обрезки. Обратите внимание, что обрезка удаляет обрезанные области изображения, поэтому обрежьте фотографию, когда вы уверены, что хотите, чтобы она выглядела. Перед кадрированием убедитесь, что у вас есть копия оригинальной фотографии на тот случай, если вам понадобится вернуться к ней.
Шаг 1
Нажмите синюю кнопку в верхнем левом углу окна Paint. Нажмите «Открыть» и выберите фотографию, которую хотите обрезать.
Шаг 2
Нажмите стрелку вниз под «Выбрать» в группе инструментов «Изображение».
Шаг 3
Нажмите инструмент «Прямоугольное выделение», если основная форма обрезки должна быть квадратной или прямоугольной.
 Нажмите на инструмент «Выбор произвольной формы», если хотите создать неправильную форму.
Нажмите на инструмент «Выбор произвольной формы», если хотите создать неправильную форму.Шаг 4
Нажмите и перетащите указатель мыши на фотографию, чтобы создать базовую форму обрезки. Сделав выбор, нажмите «Инвертировать выделение» на панели инструментов «Рисование». Нажмите «Удалить». Это очищает инвертированный выбор, удаляя ненужные части фотографии, как если бы она была обрезана.
Шаг 5
Щелкните фигуру в группе «Фигуры», чтобы сформировать другие углы в кадрировании. Paint в Windows 7 предоставляет вам выбор из нескольких предустановленных форм, включая звезды, стрелки, облака и различные геометрические формы.
Для получения неправильной формы щелкните инструмент «Многоугольник».
Шаг 6
Нарисуйте форму, где вы хотите создать другой угол обрезки. Например, нарисуйте многоугольник в одном углу фотографии, чтобы он обрезал угол под наклонным углом.
Шаг 7
Держите выбранную форму.
 Нажмите «Контур» в группе «Фигуры». Нажмите «Нет плана». Нажмите «Цвет 2» в группе «Цвета» и выберите белый (или любой другой цвет фона, который вы хотите использовать) в качестве цвета заливки. Форма, которую вы только что создали, должна появиться, чтобы обрезать фотографию под другим углом.
Нажмите «Контур» в группе «Фигуры». Нажмите «Нет плана». Нажмите «Цвет 2» в группе «Цвета» и выберите белый (или любой другой цвет фона, который вы хотите использовать) в качестве цвета заливки. Форма, которую вы только что создали, должна появиться, чтобы обрезать фотографию под другим углом.Шаг 8
Создайте больше форм, чтобы обрезать фотографию под большим углом. Убедитесь, что вы удалили контур и задали фигуру того же цвета, что и фон, обычно белый.
Шаг 9
Просмотрите отредактированное фото. Когда Paint очищает инвертированный выбор ранее, он должен был оставить пустые места вокруг изображения. Если вы хотите удалить эти пробелы, нажмите «Выбрать» в группе «Изображение», выберите область, которую вы хотите сохранить (оставляя пустые места), и нажмите «Обрезать» в той же группе инструментов.
Шаг 10
Нажмите синюю кнопку еще раз. Нажмите «Сохранить как». Выберите формат файла и сохраните файл под уникальным именем.
Угол, виды углов и их измерение
Определение.
 Угол — это часть плоскости, ограниченная двумя лучами, исходящими из одной точки, называемой вершиной угла.
Угол — это часть плоскости, ограниченная двумя лучами, исходящими из одной точки, называемой вершиной угла.Если плоскость круга разделить на 360 равных частей радиусами, то часть круга — это угловой градус, который обозначается знаком « ° » (читается — «градус»).
Следовательно, 1° = часть круга.
Круг составит * 360 = 1° * 360 = 360°.
Угол, равный плоскости круга, составляет 360° и называется полным углом.
Если плоскость круга разделить диаметром (двумя радиусами, расположенными на одной прямой линии) на две равные части, то плоскость полукруга составит угол в 360′: 2 = 180°.
Угол, равный полуплоскости круга, составляет 180° и называется развернутым углом.
Если плоскость круга разделить двумя диаметрами (горизонтальной и вертикальной линиями) на четыре равные части, то плоскость одной части составит угол в 360° : 4 = 90°.
Угол, равный четвертой части круга, составляет 90° и называется прямым углом.

Отвлекаясь от плоскости, в которой расположен круг, изобразим углы таким образом:
Углы равны, если равны их градусные меры или у них при наложении одного угла на другой совпадают вершины и соответствующие стороны углов.
Например, прямой угол (рис. 1) мы трижды развернули вокруг вершины угла, при этом на двух рисунках (рис. 2 и 4) мы передвинули вершину угла по плоскости листа.
Инструментом для измерения углов служит транспортир.
Для измерения угла следует совместить вершину угла и штрих с цифрой 0 на шкале транспортира. Одна сторона угла должна совпадать с прямой линией транспортира, на которой стоит 0, а вторая сторона угла пересекать шкалу транспортира (полуокружность с разметкой в угловых градусах).
На пересечении стороны угла и шкалы транспортира считывается градусная мера данного угла.
Мы рассмотрели полный, развернутый и прямой углы. Существует еще два типа углов: острые и тупые.
 Все острые углы имеют градусную меру в пределах: больше 0° и меньше 90°.
Все острые углы имеют градусную меру в пределах: больше 0° и меньше 90°.Например. острые углы:
Углы, градусная мера которых больше 90°, но меньше 180°*, называются тупыми углами.
Тупые углы (штриховой линией обозначен прямой угол в составе тупого угла) приведены на рис. 5, 6,7.
Чтобы построить заданный в градусной мере угол, необходимо иметь транспортир, линейку и карандаш.
Многоугольники. презентация к уроку по геометрии (8 класс) на тему
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Учитель математики МБОУ ООШ №14 города Темрюка Краснодарского края Боярко Ирина Геннадьевна Содержание урока
A C F G B ABCDEFG- многоугольник. Отрезки AB , BC, CD, DE, EF,FG, GA — смежные не лежат на одной прямой. Отрезки несмежные не имеют общих точек. Назовите несколько пар несмежных отрезков.
 D E
D EA C F G B A,B,C,D,E,F,G- многоугольника. D E вершины
C F G B AB , BC, CD, DE, EF, FG, GA — стороны многоугольника D E А
C F G B Сумма длин сторон AB , BC, CD, DE, EF, FG, GA — называется D E А периметром многоугольника Р= AB + BC + CD + DE + EF + FG + GA Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
Многоугольник, имеющий n углов называется n -угольником. Сколько сторон имеет n –угольник? Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
A C F G B соседние вершины D E -две вершины, принадлежащие одной стороне Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
C F G B D E А AC, AD, AE, AF- диагонали многоугольника, проведённые из вершины А. Определение: Отрезок, соединяющий две несоседние вершины называется диагональю.
 Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ruОпределение: Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону. Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
Внешняя область Внутренняя область
Задача 2. Сколько диагоналей имеет пятиугольник? Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
Задача. Сколько диагоналей имеет шестиугольник? Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
А Разделим этот многоугольник на несколько треугольников, проведя из вершины А все диагонали. Сколько получилось треугольников? Найти сумму углов многоугольника
Чему равна сумма углов треугольника? Найдите сумму всех углов этого пятиугольника.
 А S=180°∙ 3 =540°
А S=180°∙ 3 =540°Зависит ли сумма углов пятиугольника от: Размера? Формы? Цвета? От чего зависит эта сумма?
Сумма углов n -угольника равна S=180°∙(n -2)
Вариант 1 Вариант 2 1. Найти количество диагоналей прямоугольника 1. Найти количество диагоналей квадрата 2. Вычисли сумму всех углов прямоугольника 2. Вычисли сумму всех углов квадрата 3. Найти сумму углов выпуклого 12-угольника 3. Найти сумму углов выпуклого 8-угольника 4. Укажи номера невыпуклых многоугольников 1 2 3 4 4. Укажи номера выпуклых многоугольников 1 2 3 4 5. Найти периметр прямоугольника со сторонами 4 см и 7 см 5. Найти периметр квадрата со стороной 12 см Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
Вариант 1 Вариант 2 1. Найти количество диагоналей прямоугольника 2 1. Найти количество диагоналей квадрата 2 2. Вычисли сумму всех углов прямоугольника 360° 2. Вычисли сумму всех углов квадрата 360° 3. Найти сумму углов выпуклого 12-угольника 1800° 3.
 Найти сумму углов выпуклого 8-угольника 1080° 4. Укажи номера невыпуклых многоугольников 1 2 3 4 4. Укажи номера выпуклых многоугольников 1 2 3 4 5. Найти периметр прямоугольника со сторонами 4 см и 7 см 22см 5. Найти периметр квадрата со стороной 12 см 48 см
Найти сумму углов выпуклого 8-угольника 1080° 4. Укажи номера невыпуклых многоугольников 1 2 3 4 4. Укажи номера выпуклых многоугольников 1 2 3 4 5. Найти периметр прямоугольника со сторонами 4 см и 7 см 22см 5. Найти периметр квадрата со стороной 12 см 48 смИспользованная литература: Л.С. Атанасян, Геометрия 7-9 (учебник для общеобразовательных учреждений). – М.: Просвещение, 2005 Картинки: http://www.gifzona.ru/pozd_1s.htm http://images-photo.ru/photo/7-2-0-0-2 http://www.webman.ru/animation/main.htm
1. Многоугольник 2. Выпуклый многоугольник 3. Решение задач 4. Работа лабораторий 5. Самостоятельная работа
«Площадь прямоугольника урок» — 5 см. Начертите квадрат со стороной 5 см. 3 см. А = 5 см. Постановка цели урока. 2 способ: 3+3+3+3+3 = 3 * 5 = 15 (см2). Начертите прямоугольник со сторонами 5 см и 3 см. 5 + 5 + 5 + 5 + 5 = 5 * 5 = 25 (см 2). 1 способ: 5 + 5 + 5 = 5 * 3 = 15 (см2). Как найти площадь квадрата? В = 3 см. Гребенникова Елена Викторовна, учитель начальных классов МОУ СОШ №5 г.
 Стрежевого.
Стрежевого.«Прямоугольник ромб квадрат» — Ромб. D. Квадрат». Решение задач на готовых чертежах. Ответы к проверочному тесту. Решение задач на тему «Прямоугольник. Проверочный тест. C. A. Дано: АВСD – ромб. Теоретическая самостоятельная работа Заполнить таблицу, отметив знаки +(да), -(нет). Цель урока: Закрепить теоретический материал по теме «Прямоугольник.
«Площадь многоугольника» — 1. 7. В. С. Разминка з а д а н и е 1. 2. Запишите правильную последовательность цифр. Цвет (один или несколько)? Перед Вами поставлена задача, раскрасить дом! 3. ? 5. 4.
«Площади фигур геометрия» — S=AD*BH. b. А. Учитель: Ивниаминова Л.А. Фигуры имеющие равные площади называются равновеликими. S=(a?b):2. C. a. Материал к уроку геометрии в 8 классе. H. D. Площади фигур. Равные фигуры имеют равные площади. S=a?b.
«Математика прямоугольник 2 класс» — 39. 6. Чем похожи фигуры под №4 и №5 Чем отличаются? 1.Сосчитайте «цепочку» 90 — 45 -9 + 14 -12 +6 – 8 + 3 =. 60. 42. 45. 2.Увеличь каждое число на 3 до 60.
 Не хочется играть сегодня в прятки. Периметр прямоугольника. Геометрический материал. 57. Устный счёт. Прочитайте стихотворение.
Не хочется играть сегодня в прятки. Периметр прямоугольника. Геометрический материал. 57. Устный счёт. Прочитайте стихотворение.«Урок 2 класс Площадь прямоугольника» — Формулы. Мы – отлично учимся! Ь. Л. Ключ. Мы – старательные! Д. Математика 2 класс Урок-открытие Площадь прямоугольника. Треугольник отрезок многоугольник прямоугольник четырехугольник квадрат. А. Все у нас получится! Р — ? Площадь — ? Выражения с переменной. 8: а P = (а + b) · 2 4 – х c: 3 P = a + b + a + b P = a · 2 + b · 2 14 + y.
Устный счёт Сравните тексты задач. Чем они похожи и чем
отличаются?
На одной остановке из автобуса вышли 10 человек,
на другой – 20. На сколько меньше пассажиров
стало в автобусе?
На одной остановке из автобуса
вышло 10 человек, на другой – 20,
Сколько человек вышло из
автобуса?
Можно ли утверждать, что решения
задач одинаковы?Сообщение темы урока
Рассмотрите чертежи.
Какую закономерность вы обнаружили?
Название каких фигур вы знаете?
Какие затруднения у вас возникли?
Как можно назвать все фигуры одним
словом?
Об этом мы будем говорить. Прочтите.
Прочтите.Определение целей урока
МНОГОУГОЛЬНИК И ЕГО ЭЛЕМЕНТЫ
Определите цели урока, используя опорные слова:
Мы познакомимся с …
Мы узнаем …
Мы вспомним …
Мы будем уметь …
Мы сможем поразмышлять …
Мы познакомимся с понятием
«многоугольник», научимся находить и
обозначать его вершины.Вы уже умеете различать и изображать на
бумаге такие фигуры, как треугольник,
четырёхугольник, пятиугольник. Такие
фигуры обычно называются
многоугольниками.
Посмотрите на рисунок на С. 42
учебника.Изучение нового материала С. 42, № 1 (у.)
На кондитерской фабрике печенье
изготавливают в форме многоугольников,
изображенных в учебнике. Как можно назвать
каждый из них?
треугольник
четырёхугольник
пятиугольник
Сколько углов имеет каждая фигура?Изучение нового материала
Рассмотрим жёлтый многоугольник.

Вывод: в жёлтом многоугольнике
5 углов, 5 сторон, 5 вершин.
Сколько в нём углов?
Какой фигурой является каждая сторона?
Сколько у него сторон?
Какой фигурой является вершина?
Сколько у него вершин?Изучение нового материала
Что вы можете сказать о количестве углов,
сторон и вершин в каждом
многоугольнике?
Вывод: в любом
многоугольнике углов,
сторон и вершин поровну.Изучение нового материала
Сколько углов в семиугольнике?
Сколько вершин в десятиугольнике?
Сколько сторон в
пятнадцатиугольнике?Изучение нового материала
Как определить название этого многоугольника?
Что проще всего сосчитать?
Сосчитайте вершины многоугольника.
Как он называется?Изучение нового материала
Бывают ли одноугольники?
А двуогольники?
Какой из многоугольников имеет
наименьшее число углов?
Как называется многоугольник, у которого
100 вершин?Изучение нового материала
Давайте научимся показывать элементы
многоугольника.
Вершины – это точки.
Стороны – это отрезки.
Углы будем показывать
вращением указки.Изучение нового материала
Вершины треугольника обозначаются
буквами.
Читать обозначение можно
разными способами, начиная
с любой вершины
АВС, ВАС, САВ, ВСА,
АСВ, СВА.
В
А
СВывод
Прочитайте.
Работа по учебнику С. 43, № 2
Что изображено на рисунке?
Как называются данные
многоугольники?Работа по учебнику С. 43, № 3
Работа по учебнику С. 43, № 4
Работа в тетради С. 16, № 1
Работа в тетради С. 16, № 2
С.44, № 7 (учебник)
Найти сумму и
разность чисел: 9 и 7.
9 + 7 = 16
9–7=2С.44, № 7 (учебник)
Найти сумму и
разность чисел: 8 и 5.
8 + 5 = 13
8–5=3С.
 44, № 7 (учебник)
44, № 7 (учебник)Найти сумму и
разность чисел: 10 и 3.
10 + 3 = 13
10 – 3 = 7С.44, № 7 (учебник)
Найти сумму и
разность чисел: 7 и 7.
7 + 7 = 14
7–7=0Презентация на тему «Выпуклый многоугольник» является интерактивным учебным пособием, целью использования которого является повышение продуктивности усвоения материала по геометрии на ранних стадиях ее изучения. Правильное и интересное преподнесение информации являются залог успеха для любого учителя, ведь учащиеся данной возрастной категории нуждаются в том, чтобы информация, которую они получают, была дана им в достаточно интересной и легкой для понимания форме.
Удачно выполненные графические изображения привлекут внимание учащихся, а у учителя не будет необходимости выполнять большое количество рисунков на доске с помощью мела, что значительно сохранит время на уроке, которое в дальнейшем можно будет потрать на изучение дополнительного интересного материала.

После слайда, содержащего название презентации, следует слайд, на котором представлены два различных многоугольника. Над изображениями вниманию учащихся представлено определение, написанное крупным шрифтом и яркими цветами, что, несомненно, привлечет внимание и хорошо запечалится в памяти учащихся.
слайды 1-2 (Тема презентации «Выпуклый многоугольник», определение выпуклого многоугольника)
Определение поясняет учащимся, что собственно является выпуклым многоугольником. Изучив данное определение, учащиеся должны понять, что фигура, изображенная справа, и является выпуклым многоугольником, что нельзя сказать о многоугольнике, изображенном слева. То, что два разных многоугольника представлены на одном слайде является очень удачным, так как учащиеся смогут провести сравнительный анализ двух фигур, что позволит еще раз закрепить в памяти изученное определение и научиться применять его на практике.
На третьем слайде презентации также имеется изображение многоугольника, который красными отрезками разбит на составляющие его треугольники.
 Если посчитать количество сторон многоугольника и количество треугольников, на которые он разбит, то легко можно сделать вывод о том, что представленные многоугольник состоит из треугольников, число которых на два меньше, чем сторон прямоугольника. Данные сведения необходимы для того, чтобы у учащихся была возможность посчитать сумму углов выпуклого многоугольника, содержащего любое количество вершин.
Если посчитать количество сторон многоугольника и количество треугольников, на которые он разбит, то легко можно сделать вывод о том, что представленные многоугольник состоит из треугольников, число которых на два меньше, чем сторон прямоугольника. Данные сведения необходимы для того, чтобы у учащихся была возможность посчитать сумму углов выпуклого многоугольника, содержащего любое количество вершин.слайд 3 (сумма углов)
Исходя из знаний, полученных на более ранних сроках изучения геометрии о том, что сумма сторон треугольника всегда равна ста восьмидесяти градусам. И новой информации о том, на сколько треугольников разбивается многоугольник, учащиеся с помощью учителя могут сделать вывод о том, что сумма углов выпуклого многоугольника равна сумме сторон треугольников, на которые он разбит, умноженной на сто восемьдесят градусов.
Данная презентация на тему «Выпуклый многоугольник» на понятном и доступном уровне преподносит учащимся основную информацию, касающуюся выпуклого многоугольника.
 Она может использоваться не только на уроке в школе, но также является отличным материалом для самостоятельного изучения учащимися дома.
Она может использоваться не только на уроке в школе, но также является отличным материалом для самостоятельного изучения учащимися дома.Бывшая учительница математики предложила решение нерешаемой задачи — Российская газета
В челябинскую редакцию «РГ» обратилась читательница из Миасса с очень необычной проблемой. Пенсионерка, в прошлом учительница математики, Ляля Зарипова все свободное время посвящает любимому предмету и пытается решить еще не решенные задачи — по ее собственному выражению, стереть белые пятна, существующие в математике с древних времен. Однако, сумев найти решение одной из таких задач, она уже более двух лет безуспешно старается привлечь к нему внимание общественности.
Вопреки вердикту
Одна из старейших математических загадок, доставшаяся человечеству от грека Архимеда, получила название задачи о трисекции угла. Великий мыслитель и один из отцов геометрии попытался разделить угол на три равные части с помощью циркуля и линейки. Однако найти решение не смог и завещал эту загадку ученикам и потомкам.

Отметим, что любой школьник сегодня легко разделит угол на две половины. Линейки и циркуля для этого вполне достаточно. Без особого труда можно разбить на три равные части прямой угол, встроив в него равносторонний треугольник. Автор этих строк справился с задачкой, потратив не более пяти минут. Однако разделить любой угол на три равные части ученые до сих пор не смогли.
Еще в 1837 году известный французский математик Пьер Ванцель, проигнорировав условия Архимеда о циркуле и линейке, попытался найти «трисекцию угла» алгебраическим путем и… потерпел фиаско. Пришел к выводу, что задача нерешаема. В дальнейшем решение искать просто перестали. А позже Французская академия наук вынесла официальный вердикт о том, что эту задачу решить невозможно, и исключила ее из всех учебников и справочников того времени.
С тех пор о головоломке, некогда занимавшей лучшие математические умы, забыли. Ляля Гиззатовна искала «ключ» несколько лет и, перепробовав множество путей, нашла простое и блестящее решение, к которому, судя по оставшимся в истории записям, шел сам Архимед, но довести его до конца не сумел.

По мнению учительницы, чтобы разделить угол на три равные части, нужно провести из его вершины окружность, отложить за ее пределами еще один радиус на биссектрисе, делящей этот угол пополам, и получить так называемый внешний угол. Он и будет в три раза меньше заданного угла, то есть станет одной из трех секций из условия задачи.
Последние три сотни лет решение даже не искали, а все это время математика шла семимильными шагами. Возможно, стоит попробовать снова?
Более того, автор геометрического подхода уверена: откладывая на биссектрисе нужное число радиусов, угол можно разделить не только на три, но и на пять, семь и девять частей — другими словами, разделить его на любое нечетное число. А это, в свою очередь, позволит найти решение еще одной математической головоломки — вписать в окружность любой правильный многоугольник. В справочниках до сих пор утверждается, что вписать правильные многоугольники, имеющие семь и девять сторон, в окружность невозможно. Ну разве это не открытие?
Однако, прежде чем понять, что решение единственно верное, Ляле Гиззатовне нужно было найти для него теоретическое обоснование.
 Для этого она сформулировала и доказала три теоремы, подтверждающие правильность подхода. И только после этого поделилась с миром своим открытием.
Для этого она сформулировала и доказала три теоремы, подтверждающие правильность подхода. И только после этого поделилась с миром своим открытием.Хождение по академиям
— Однако рассказать о нем оказалось сложнее, чем сделать, — посетовала Ляля Гиззатовна. — С января 2018 года звонила, писала, умоляя чиновников от науки об одном — выслушайте! Но наталкивалась на глухую стену непонимания. Письма нераспечатанными возвращали назад. В телефонных переговорах после слов о том, что мне удалось найти трисекцию угла, обещали перезвонить и не перезванивали. Вероятно, принимали за сумасшедшую. Ведь во всех учебниках написано, что решения у этой задачи нет…
Сначала учительница обратилась в Минобрнауки РФ, однако оттуда ее перенаправили в Российскую академию наук. В РАН сослались на реорганизацию и попросили написать в математический институт имени В.А. Стеклова, где объяснили, что занимаются высшей математикой, а вопросы, касающиеся элементарной математики, — компетенция специально созданного института по работе с научными открытиями.

— Директор этого учреждения, услышав голос «очередного изобретателя вечного двигателя», посоветовал получше изучить геометрию, в которой черным по белому записано, что задача о трисекции угла не имеет решения. А когда я начала его убеждать, посоветовал сначала опубликовать работу в каком-нибудь научном издании, а уж потом отнимать время у академиков, — вспоминает этот разговор учительница.
Дальше была переписка с Казанским и Новосибирским отделениями РАН, откуда Ляля Гиззатовна получила выдержку из Википедии. В итоге письмо учительницы вернулось обратно в Минобрнауки РФ, и круг замкнулся…
Эксперимент
Чтобы помочь Ляле Гиззатовне донести свои мысли до широкой общественности, предлагаем ей прямо в редакции вооружиться циркулем и линейкой. Снимаем на видео, как она делит угол на три равные части, а затем договариваемся о встрече с известным челябинским ученым, академиком РАН Сергеем Матвеевым и его коллегами-математиками из Челябинского госуниверситета.
Сначала предложение посмотреть видео с решением задачи о трисекции угла встречает тот же отпор, с которым в течение двух лет сталкивалась педагог.

— Этой проблемой занималось не одно поколение математиков, — возмущается Сергей Матвеев. — Какое бы решение ни предложили, оно однозначно неверное. Иначе это действительно сенсация, и с ней можно претендовать на Нобелевскую премию.
— Но ведь, если верить истории, последние две сотни лет решение даже не искали, а все это время математика шла семимильными шагами, — пытаемся привести аргумент Ляли Гиззатовны. — Возможно, стоит попробовать снова? Ведь в ХIХ веке могли и ошибаться?
— Мир остался прежним, как и его законы, — отметает довод доцент кафедры математики Филипп Кораблев. — Если вы бросите камень, он на Марс не улетит. Мы, конечно, можем посмотреть видео и, возможно, даже не обнаружим в этом решении ошибку, но она там обязательно есть. Мы бы посоветовали учительнице поискать ее самой!
Вот как! И это экспертное мнение? Проявив немалую настойчивость, нам все-таки удается уговорить математиков потратить пять-семь минут на видео. Несмотря на высказанное недоверие, происходящее на экране вызывает у них неподдельный интерес.

Сотрудники кафедры поэтапно перематывают ролик и ищут «вкравшуюся» ошибку, обмениваясь оживленными репликами: «Если решение строится на том, что это ромб, то оно неверно, поскольку две его вершины находятся на окружности», «А действительно ли эти хорды проходят через центр окружности? Видите, как дрогнула рука, когда она их чертила?».
И, хотя явной ошибки, подрывающей все математические устои, как и предупреждал Филипп Кораблев, с ходу найти не удается, они остаются при своем мнении: решение не может быть правильным, потому что доказано обратное! Именно эту мысль и попросил как можно деликатнее донести до Ляли Гиззатовны Сергей Матвеев. А потом добавил:
— А вообще… Было интересно…
Отложите гаджеты
Рассказывая о невозможности решить задачу Архимеда, доцент Кораблев вспомнил, как в школе ее предложила учительница математики — видимо, просто устала от класса:
— Мы пол-урока ломали головы и выдвигали свои версии, конечно, изначально неверные. И только после узнали, что она просто пошутила и водила нас за нос.

Но ведь как минимум один человек из этого класса все-таки стал математиком, разве не так?
Сегодня увлечь детей настолько, чтобы они хотя бы на пять минут отложили в сторону любимые гаджеты, — задачка не из простых. И не всякая школа способна ее решить. Интерес к естественным наукам, физике и математике, царивший в эру завоевания космоса, сильно упал. И пробудить его могли бы подвижники-учителя, такие как Архимед, преподаватель математики доцента Кораблева или скромная пенсионерка из Миасса Ляля Зарипова.
Энергии и увлеченности этого человека можно позавидовать. В 86 лет Ляля Гиззатовна продолжает увлекать любимым предметом окружающих. Наверное, поэтому к ней по-прежнему обращаются с просьбой подтянуть детей по математике. Ведь после ее уроков ученик начинает стараться понять, а не зазубрить, решить, а не списать из Интернета…
P. S.
Возможно, Ляля Гиззатовна и правда достойна Нобелевской премии? «РГ» обращается ко всем, кто силен в математике и геометрии: давайте найдем ошибку в решении, предложенном учительницей (свои варианты присылайте по адресу [email protected]).
 А может, никакой ошибки нет? Решив задачу о трисекции угла, Ляля Гиззатовна пытается разгадать загадку простых натуральных чисел…
А может, никакой ошибки нет? Решив задачу о трисекции угла, Ляля Гиззатовна пытается разгадать загадку простых натуральных чисел…Определение, стороны, углы (обычные и нестандартные)
Что такое семиугольник?
Гептагон — это 7-сторонний многоугольник с 7 внутренними углами, которые в сумме составляют 900 °. Название семиугольник происходит от греческих слов hepta- для семи и gon- для сторон. Семигранник также называют 7-угольником или септагоном ( септа- на латыни означает семь).
Форма шестиугольника
Форма семиугольника — это плоская или двумерная форма, состоящая из семи прямых сторон, семи внутренних углов и семи вершин.Форма семиугольника может быть правильной, неправильной, вогнутой или выпуклой.
Вот некоторые дополнительные свойства формы семиугольника:
- Все семиугольники имеют внутренние углы в сумме 900 °
- Все семиугольники имеют внешние углы в сумме 360 °
- Все семиугольники можно разделить на пять треугольников
- Все семиугольники имеют 14 диагоналей (отрезки прямых, соединяющие вершины)
Стороны семиугольника
Стороны семиугольника должны быть прямыми и пересекаться, чтобы образовать семь вершин, замыкающихся в пространстве.
 Семь сторон семиугольника встречаются, но не пересекаются и не пересекаются друг с другом.
Семь сторон семиугольника встречаются, но не пересекаются и не пересекаются друг с другом.Как и у других двумерных фигур, стороны семиугольника могут иметь разную длину, что создает неправильный семиугольник. Либо стороны могут совпадать, образуя правильный семиугольник
семиугольник с пересекающимися сторонами называется гептаграммой.
Углы шестиугольника
У семиугольника есть семь внутренних углов в сумме 900 ° и семь внешних углов в сумме 360 °. Это верно как для правильных, так и для неправильных семиугольников.
В правильном семиугольнике каждый внутренний угол составляет примерно 128,57 °.
Ниже приведена формула для определения меры любого внутреннего угла правильного многоугольника (n = количество сторон):
Мы знаем, что все семиугольники (или септагоны) имеют 7 сторон, поэтому можем подставить это в нашу формулу:
(180 ° × 7) — 360 ° 7 =
1260 ° — 360 ° 7 =
900 ° 7 ≈ 128,5714 °
Диагонали семиугольника
семиугольника имеют 14 диагоналей.
 Для выпуклых семиугольников все диагонали будут внутри формы. Для вогнутых семиугольников по крайней мере одна диагональ будет за пределами формы.
Для выпуклых семиугольников все диагонали будут внутри формы. Для вогнутых семиугольников по крайней мере одна диагональ будет за пределами формы.Обычный семиугольник
Вот изображение правильного семиугольника . У правильного семиугольника семь совпадающих сторон, семь вершин и семь совпадающих внутренних углов:
Как указано решеткой, правильный семиугольник на картинке выше имеет равные стороны.
Выпуклый шестиугольник
Правильный семиугольник — это всегда выпуклый семиугольник.У выпуклого семиугольника внутренние углы не превышают 179 °:
Поскольку внутренний угол не превышает 179 °, диагональ не может лежать за пределами многоугольника.
Неправильный семиугольник
Вот неправильный семиугольник , что означает, что его семь сторон не совпадают, а его семь внутренних углов не идентичны:
Как и другие неправильные многоугольники, неправильные семиугольники могут быть выпуклыми или вогнутыми, как на изображении семиугольника выше.

Вогнутый семиугольник
Вогнутый семиугольник имеет как минимум один внутренний угол больше 180 °, и он имеет как минимум одну диагональ, выходящую за пределы многоугольника:
Площадь семиугольника
Площадь правильного семиугольника можно найти по формуле:
Эта формула приблизительно равна A = 3. 643a2
В обеих формулах a = длина стороны.
Гептагон в реальной жизни
Есть много примеров семиугольника в реальной жизни, например, на двух картинках ниже:
Подобно другим геометрическим фигурам, таким как восьмиугольник, шестиугольник и четырехугольник, семиугольные фигуры можно встретить в искусственных объектах и в природе.
Heptagon Quiz
- Для любого семиугольника какова сумма его внутренних углов?
- Сколько вершин у любого семиугольника?
- Сколько диагоналей вы можете нарисовать для любого семиугольника?
- Может ли семиугольник иметь девять сторон?
- Ниже представлены несколько полигонов.
 Сначала выберите все, что являются семиугольниками. Затем для каждого выбранного вами семиугольника определите, является ли он правильным или неправильным, а затем будет ли он вогнутым или выпуклым:
Сначала выберите все, что являются семиугольниками. Затем для каждого выбранного вами семиугольника определите, является ли он правильным или неправильным, а затем будет ли он вогнутым или выпуклым:
Пожалуйста, попробуйте работу, прежде чем искать ответы!
- Сумма внутренних углов семиугольника всегда составляет 900 °.
- У всех семиугольников семь вершин, так же как у них семь сторон и семь внутренних углов.
- У всех семиугольников будет 14 диагоналей; если диагональ лежит вне многоугольника, вы знаете, что семиугольник вогнутый.
- Нет, у семиугольников всего семь сторон. 9-сторонний многоугольник называется шестигранником.
- Из восьми фигур только пять семиугольников. Два — правильные выпуклые семиугольники. Три — неправильные вогнутые семиугольники. Бонус: одна фигура в сетке — пятиугольник.
Следующий урок:
Десятиугольник
Введение, типы, формулы и решенные примеры
Как правило, многоугольник с n сторонами имеет:
n внутренних углов.

Сумма внутренних углов = (n — 2) × 180 °
Каждый внутренний угол правильного многоугольника = \ [\ frac {(n-2) х 180⁰} {n} \]
Сумма внешних углов = 360 °
В этой статье мы подробно узнаем о семигранном многоугольнике, называемом «семиугольник», с его правильным определением, формой, количеством сторон, свойствами, его формулой периметра и площади. .
Определение семиугольника
(изображение скоро будет обновлено)
Семиугольник — это многоугольник, у которого семь сторон и семь углов.Слово «семиугольник» состоит из двух слов, а именно «Гепта» и «Гония», что означает семь углов.
Иногда семиугольник также называют «септагоном».
Поскольку у семиугольника 7 сторон, следовательно,
Сумма внутренних углов = (n — 2) × 180 °
= (7-2) × 180 ° = 5 × 180 °
= 900 °
Каждый внутренний угол правильного семиугольника = \ [\ frac {(n-2) х 180⁰} {n} \]
= \ [\ frac {(7-2) х 180⁰} {5 } \] = \ [\ frac {900} {5} \]
= 128.
 571 °
571 °Сумма внешних углов = 360 °
Формы семиугольника
В зависимости от сторон, углов и вершин, формы семиугольника классифицируются как:
Правильные семиугольники
- Неправильные семиугольники
Обычный семиугольник
(изображение будет обновлено в ближайшее время)
Чтобы быть правильным семиугольником, семиугольник должен иметь:
семь конгруэнтных сторон (стороны равной длины)
семь конгруэнтных внутренних углов (каждый измеряет 128. 571 °)
семь конгруэнтных внешних углов 51,428 °
Примечание: правильные семиугольники не имеют параллельных сторон.

Неправильный семиугольник
Неправильный семиугольник — это семиугольник, имеющий разные длины сторон и размеры углов. (изображение будет обновлено в ближайшее время)
Неправильные семиугольники могут быть выпуклым семиугольником или вогнутым семиугольником:
Выпуклый семиугольник — семиугольник, не имеющий внутренних углов более 180 °.
Вогнутый семиугольник — семиугольник, внутренний угол которого превышает 180 °.(изображение будет обновлено в ближайшее время)
Свойства Heptagon
У него семь сторон, семь вершин и семь внутренних углов.
Имеет 14 диагоналей.
Сумма всех внутренних углов составляет 900 °.
Сумма внешних углов составляет 360 °.

У правильного семиугольника все семь сторон равной длины.
Каждый внутренний угол правильного семиугольника равен 128.571 °.
Неправильные семиугольники имеют разную длину сторон и разную величину угла.
Все диагонали выпуклого семиугольника лежат внутри семиугольника.
некоторые диагонали вогнутого семиугольника могут лежать вне семиугольника.
Периметр семиугольника
Периметр семиугольника — это сумма длин его семи сторон.
Для правильного семиугольника, так как длины всех семи сторон равны.
Следовательно, периметр правильного семиугольника = 7 × (длина стороны) единиц.
Площадь семиугольника
Площадь семиугольника — это область, охватываемая сторонами семиугольника.

Для правильного семиугольника его площадь можно рассчитать по следующей формуле:
(изображение будет скоро обновлено)
Если заданы мера длины стороны и апофемы, то:
центр правильного многоугольника под прямым углом к любой из его сторон.)
Площадь семиугольника = \ [\ frac {7} {2} \] × (длина стороны) × (апофема) единиц 2
OR,
Площадь семиугольника = \ [\ frac {1} {2} \ ] × (периметр семиугольника) × (апофема) единиц2
Если дана только мера длины стороны, то:
Площадь семиугольника = \ [\ frac {7} {4} \] кроватка \ [ \ frac {π} {7} \] ⁰ × (длина стороны) 2 единицы 2
Где, детская кроватка \ [\ frac {π} {7} \] ⁰ = детская кроватка 25,714⁰ = 2,0765
OR,
Площадь семиугольник = 3,634 × (длина стороны) 2 единицы 2
Решенные задачи:
Q.
 1. Найдите периметр и площадь правильного семиугольника со стороной 7 см?
1. Найдите периметр и площадь правильного семиугольника со стороной 7 см?Решение: Дано, сторона семиугольника = 7 см
Периметр правильного семиугольника = 7 × (длина стороны) единиц
= 7 × 7 см
= 49 см
А,
Площадь семиугольника = 3,634 × (длина стороны) 2 шт.2
= 3.634 × (7) 2
= 178,066 см2
Следовательно, периметр и площадь правильного семиугольника со стороной 7 см составляют 40 см и 140 см2 соответственно.
Полигоны
Многоугольник — это плоская форма с прямыми сторонами.
Это многоугольник?
Многоугольники — это двумерные фигуры. Они состоят из прямых линий, а форма «замкнута» (все линии соединяются).
Многоугольник
(прямые стороны)Не многоугольник
(имеет кривую)Не a Многоугольник
(открытый, не закрытый)Многоугольник происходит от греческого языка.
 Poly- означает «много», а -угольник означает «угол».
Poly- означает «много», а -угольник означает «угол».Типы полигонов
Обычные или нестандартные
У правильного многоугольника все углы равны и все стороны равны, в противном случае он неправильный
Обычный Нерегулярное Вогнутая или выпуклая
Выпуклый многоугольник не имеет углов, направленных внутрь.Точнее, внутренний угол не может быть больше 180 °.
Если какой-либо внутренний угол больше 180 °, тогда многоугольник вогнутый . ( Подумайте: в вогнутой части есть «пещера» )
Выпуклый вогнутая Простой или сложный
Простой многоугольник имеет только одну границу и не пересекает себя.
 сложный полигон пересекает сам себя! Многие правила, касающиеся многоугольников, не работают, когда они сложные.
сложный полигон пересекает сам себя! Многие правила, касающиеся многоугольников, не работают, когда они сложные.Простой многоугольник
(это пятиугольник)Сложный многоугольник
(также пятиугольник)Другие примеры
Шестигранник неправильной формы Вогнутый восьмиугольник
Сложный многоугольник
(«звездообразный многоугольник»,
в данном случае пентаграмма)Играй с ними!
Попробуйте интерактивные многоугольники… сделайте их правильными, вогнутыми или сложными.
Имена полигонов
С помощью этого метода можно делать имена:
Стороны
Начать с .  ..
..20
Икоси … 30
Triaconta… 40
Тетраконта … 50
Пентаконта … 60
Гексаконта … 70
Heptaconta… 80
Октаконта … 90
Эннеаконта … 100 Гекта … и т. Д. Стороны
… закончить с +1
… шестигранник +2
… digon +3
… тригон +4
…тетрагон +5
… пятиугольник +6
… шестигранник +7
… семиугольник +8
… восьмиугольник +9
… enneagon Пример: 62-сторонний многоугольник — это гексаконтадигон
НО для многоугольников с 13 и более сторонами нормально (и проще) написать « 13-угольник », « 14-угольник » .
 .. « 100-угольник» и т. Д.
.. « 100-угольник» и т. Д.Вспоминая
Четырехсторонний (4 стороны)
A Quad Велосипед с 4 колесамиПентагон (5 сторон)
« Пентагон » в Вашингтоне, округ Колумбия, имеет 5 сторонШестиугольник (6 сторон)
H oneycomb имеет H эксагоновСептагон (7 сторон)
Think Sept agon — это «Seven- agon»
Восьмиугольник (8 сторон)
Гной Octo имеет 8 щупалецNonagon (9 сторон)
Think Non agon is a «Nine- agon»
Десятиугольник (10 сторон)
Think Dec agon имеет 10 сторон,
точно так же, как наша Dec imal система имеет 10 цифрПериметр многоугольника — веб-формулы
Периметр многоугольника:
Многоугольник определяется как плоская фигура, заключенная в замкнутый контур или замкнутый круг.Как правило, периметр определяется как путь, окружающий область.
 Периметр многоугольника — это сумма длин его сторон.
Периметр многоугольника — это сумма длин его сторон.Типы многоугольников
· Квадрат
· Прямоугольник
· Параллелограмм
· Треугольник
· Ромб
· ТрапецияСписок форм многоугольника
Форма
Описание
Многоугольник
Замкнутая фигура, состоящая из отрезков прямой, каждый из которых пересекается ровно с двумя другими отрезками.
Четырехсторонний
4-сторонний многоугольник
Квадрат
Четырехугольник, все стороны которого равны по длине и образуют прямые углы.

Треугольник
Трехсторонний многоугольник (сумма внутренних углов = 180 °)
Прямоугольник
Четырехсторонний многоугольник со всеми прямыми углами.
Параллелограмм
4-сторонний многоугольник с двумя парами параллельных сторон.
Пентагон
5-сторонний многоугольник (на рисунке показан правильный шестиугольник, где «правильный» означает, что все стороны равны по длине)
Шестигранник
6-сторонний многоугольник
Гептагон
7-сторонний многоугольник
Восьмиугольник
8-сторонний многоугольник
Примечания :
Периметры квадрата и ромба равны
Периметры прямоугольника и параллелограмма равны
Периметры многоугольников с более чем шестью сторонами могут быть найдены с помощью аналогичной формулы периметра.
· Гептаган (Многоугольник с семью сторонами) периметр равен сумме длин семи сторон
· Восьмиугольник (Многоугольник с восемью сторонами) периметр равен сумме длин восьми сторон
· Nenagon (Многоугольник с девятью сторонами) периметр равен сумме длин девяти сторон
· Десятиугольник (многоугольник с десятью сторонами) периметр равен сумме длин десяти сторонФигуры, которые не считаются многоугольниками:
Рисунок ниже не является многоугольником, так как это не замкнутая фигура:Рисунок ниже не является многоугольником, так как он не состоит из отрезков линии:
Рисунок ниже не является многоугольником, так как его стороны не пересекаются ровно в двух местах каждый:
Правильный многоугольник :
Многоугольник, все стороны которого равны и имеют равные углы.Сумма углов многоугольника со сторонами n , где n равно 3 или более, составляет 180 ° × ( n — 2) градусов.Примеры правильных многоугольников: Равносторонний треугольник , Квадрат и Ромб
Периметр правильного многоугольника определяется по формуле:
P = ns
Где n — количество сторон, а s — длина каждая сторона.
Неправильный многоугольник:
Многоугольник, у которого не равны стороны и разные внутренние углы, называется неправильным многоугольником.
Периметр неправильного многоугольника определяется простым сложением длины каждой стороны. На рисунках ниже показаны многоугольники, которые не считаются правильными многоугольниками:Пример 1: Найдите периметр следующей фигуры
Решение :
AB = FE + DC = 5 + 5 = 10 см
BC = AF + ED = 4 + 4 = 8 смP = AB + BC + CD + DE + EF + FA
P = 10 + 8 + 5 + 4 + 5 + 4
P = 36 смПример 2: Найдите периметр правильного десятиугольника со стороной 5 см
Решение :
Количество сторон в десятиугольнике (n) = 10 и стороне s = 5 см
Периметр десятиугольника:
P = нс
P = 10 x 5
P = 50 смПример 3: Найдите периметр двенадцатиугольника со стороной 7 см.

Решение :
Количество сторон в двенадцатиугольнике (n) = 12 и стороне s = 7 см
Периметр двенадцатиугольника:
P = нс
P = 12 x 7
P = 84 смПример 4: Каков периметр рисунка ниже, если его площадь составляет 27 футов 2 ?
Решение : Периметр фигуры = AB + BD + DE + EA
· Длина стороны AB = 2 фута
· Длина стороны DE = 4 фута
· Длина стороны EA = 5 футовПлощадь трапеции = ½ × высота × (сумма размеров параллельных сторон)
Подставляя значения, получаем:
Площадь = (12) × FC × (AE + BD)
Площадь = (12) × 3 × (5 + BD)Так как площадь задана, мы теперь имеем:
27 футов 2 = ½ × 3 × (5 + BD)Умножить каждую сторону на 2
54 футов 2 = 3 × (5 + BD)Разделить каждую сторону на 3
18 ft = 5 + BDВычитая 5 с обеих сторон
BD = 13 ftИ теперь мы можем определить периметр трапеции:
Периметр фигуры = 2 + 13 + 4 + 5 = 24 фута.
Пример 5: Найдите периметр правильного пятиугольника, длина стороны которого равна 4 см.
Решение :
Мы знаем, что периметр правильного многоугольника определяется как: P = ns
Поскольку пятиугольник имеет 5 сторон, мы имеем: n = 5
Итак, периметр правильного пятиугольника равен 5 * 4 = 20 см.Пример 6 : Каков периметр правильного шестиугольника с длиной стороны 3,5 см?
Решение :
Учитывая, что: s = 3.5см.
У правильного шестиугольника 6 сторон одинаковой длины.Следовательно, периметр правильного шестиугольника равен:
P = 6 * длина
P = 6 * 3,5
P = 21 смОнлайн-калькулятор периметра
Название геометрических фигур — многоугольники, многогранники
Поиск инструмента
Название геометрических фигур
Инструмент для поиска названия геометрических фигур. Многоугольники — это геометрические фигуры в плоскости 2D, а многогранники — это геометрические фигуры в пространстве 3D
Результаты
Название геометрических фигур — dCode
Тег (-ы): Geometry
Поделиться
dCode и др.

dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !Рекламные объявления
Ответы на вопросы (FAQ)
Как называется многоугольник с…?
Укажите dCode количество сторон и он найдет имя.
Пример: 6: HEXAGON
12: DODECAGONВ более общем смысле, многоугольника записываются с префиксом, указывающим их количество сторон, и суффиксом -угольник .
Вот список в виде таблицы всех различных правильных геометрических форм 2D-плоскости (таблица имен n-сторонних многоугольников ):
Как называется многогранник с…?
Укажите количество граней, и он найдет имя трехмерной геометрической фигуры.
Пример: 6: HEXAHEDRON
Пример: 12: DODECAHEDRON
Вот таблица всех правильных геометрических форм / многогранников трехмерного пространства (таблица названий n-гранных многогранников ):
Как выучить геометрические фигуры?
Некоторые ресурсы для детей отлично подходят для изучения фигур и других геометрических фигур, например, здесь (ссылка)
Какие многоугольники обладают осевой симметрией?
Все правильные многоугольники имеют по крайней мере одну осевую симметрию.

Правильный многоугольник с таким количеством осей симметрии, сколько у него сторон.
Оси симметрии проходят через центр многоугольника и центр каждой стороны или каждой вершины / угла.
Какие многоугольники имеют центральную симметрию?
Все правильные многоугольника с четным номером стороны имеют центральную симметрию (центр многоугольника ). Многоугольники с нечетным числом сторон не имеют центральной симметрии.
Что такое многогранник?
Многогранник — это обобщение многоугольника / многогранника на все измерения.
Задайте новый вопрос
Исходный код
dCode сохраняет право собственности на исходный код онлайн-инструмента «Имя геометрических фигур». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / бесплатно), любого алгоритма, апплета или фрагмента «Имя геометрических фигур» (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любое другое » Имя функции геометрических фигур (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести), написанное на любом информационном языке (Python, Java, PHP, C #, Javascript, Matlab и т.
 Д.)), и никакая загрузка данных, скрипт, копипаст или доступ к API для «Имя геометрических фигур» не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.
Д.)), и никакая загрузка данных, скрипт, копипаст или доступ к API для «Имя геометрических фигур» не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.Нужна помощь?
Пожалуйста, посетите наше сообщество dCode Discord для запросов о помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!Вопросы / комментарии
Сводка
Похожие страницы
Поддержка
Форум / Справка
Ключевые слова
многоугольник, многогранник, многогранник, геометрия, евклидово, форма, префикс, геометрический, сторона, грань, форма, 2d, 3d, имя, список
Ссылки
Источник: https: // www.dcode.fr/geometric-shapes
© 2021 dCode — Лучший «инструментарий» для решения любых игр / загадок / геокэшинга / CTF.
Как создать шестиугольник со скругленными углами в фотошопе с помощью инструмента многоугольник?
Как создать шестиугольник со скругленными углами в фотошопе с помощью инструмента многоугольник? — Обмен стеками графического дизайна
Сеть обмена стеков
Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.

Посетить Stack Exchange
- 0
- +0
- Авторизоваться Зарегистрироваться
Graphic Design Stack Exchange — это сайт вопросов и ответов для профессионалов, студентов и энтузиастов графического дизайна.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществу
Кто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 65к раз
Как создать шестиугольник со скругленными углами в Photoshop с помощью инструмента многоугольник?
Эрик
1,93311 золотых знаков99 серебряных знаков1515 бронзовых знаков
Создан 02 июл.

Ахмед Амроахмед Амро
29711 золотой знак22 серебряных знака1414 бронзовых знаков
Выбрав инструмент «Многоугольник», щелкните маленький значок шестеренки на панели управления a и затем отметьте опцию Smooth Corners .
Photoshop CC или CS6:
Photoshop CS5 или CS4:
Вам также может потребоваться настроить параметры «Звездочка» ….
Создан 02 июля ’13 в 23: 352013-07-02 23:35
Скотт Скотт
187k1919 золотых знаков253253 серебряных знака504504 бронзовых знака
14
у меня есть идея, попробуйте это создать шестиугольник, добавить толстую границу из стиля, как показано на изображении, и следуйте инструкциям 2 и 3
Создан 19 мая ’14 в 10: 572014-05-19 10:57
1 Очень активный вопрос .
 Заработайте 10 репутации, чтобы ответить на этот вопрос. Требование репутации помогает защитить этот вопрос от спама и отсутствия ответов.
Graphic Design Stack Exchange лучше всего работает с включенным JavaScript
Заработайте 10 репутации, чтобы ответить на этот вопрос. Требование репутации помогает защитить этот вопрос от спама и отсутствия ответов.
Graphic Design Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
Внутренние углы многоугольника
Быстрые определения
Давайте пройдемся по нескольким ключевым словам, чтобы мы все оказались на одной странице.Помните, что многоугольник — это двухмерная фигура, стороны которой нарисованы прямыми линиями (без кривых), которые вместе образуют замкнутую область. Каждая точка многоугольника, где встречаются две стороны, называется вершиной . В каждой вершине есть внутренний угол многоугольника.
 Квадрат, например, имеет четыре внутренних угла по 90 градусов каждый. Если квадрат представляет ваш класс, внутренние углы — это четыре угла комнаты.
Квадрат, например, имеет четыре внутренних угла по 90 градусов каждый. Если квадрат представляет ваш класс, внутренние углы — это четыре угла комнаты.Сумма внутренних углов
В дальнейшем, если многоугольник имеет x сторон, сумма S мер степени этих x внутренних сторон определяется формулой S = (x — 2) (180) .
Например, треугольник имеет 3 угла, которые в сумме составляют 180 градусов. У квадрата 4 угла, которые в сумме составляют 360 градусов. Для каждой дополнительной стороны, которую вы добавляете, вы должны добавить еще 180 градусов к общей сумме.
{include ad_line.html%}
Давайте поговорим о диагонали минутку. Что вообще такое диагональю ? Диагональ — это отрезок линии, соединяющий две непоследовательных вершин многоугольника. Это все линии между точками в многоугольнике, если не считать те, которые также являются сторонами многоугольника.На картинке ниже BD — это диагональ.
 Как видите, отрезок BD делит четырехугольник ABCD на два треугольника. Сумма углов в этих треугольниках (180 + 180 = 360) равна сумме всех углов прямоугольника (360).
Как видите, отрезок BD делит четырехугольник ABCD на два треугольника. Сумма углов в этих треугольниках (180 + 180 = 360) равна сумме всех углов прямоугольника (360).Пример 1
Четырехугольник ABCD, конечно, имеет четыре угла. Эти четыре угла находятся в соотношении 2: 3: 3: 4. Найдите градус наибольшего угла четырехугольника ABCD.
Что мы знаем?
У нас есть четыре неизвестных угла, но информация об их отношении друг к другу.Поскольку мы знаем, что сумма всех четырех углов должна составлять 360 градусов, нам просто нужно выражение, которое складывает наши четыре неизвестных угла и устанавливает их равными 360. Поскольку они находятся в соотношении, у них должен быть некоторый общий множитель, который нам нужен найти, называется x.
Шагов:
- Добавьте условия 2x + 3x + 3x + 4x
- Приравнять сумму слагаемых к 360
- Решить для x
- Определите угол в градусах.
Решить
2x + 3x + 3x + 4x = 360
12x = 360
x = 360/12
x = 30Несмотря на то, что мы знаем x = 30, мы еще не закончили.
 Умножаем 30 на 4, чтобы найти наибольший угол. Поскольку 30 умножить на 4 = 120, наибольший угол составляет 120 градусов. Аналогично, другие углы равны 3 * 30 = 90, 3 * 30 = 90 и 2 * 30 = 60.
Умножаем 30 на 4, чтобы найти наибольший угол. Поскольку 30 умножить на 4 = 120, наибольший угол составляет 120 градусов. Аналогично, другие углы равны 3 * 30 = 90, 3 * 30 = 90 и 2 * 30 = 60.Правильные многоугольники
Правильный многоугольник равносторонний. Все его углы имеют одинаковую меру. Он также равносторонний. Все его стороны имеют одинаковую длину. Квадрат — это правильный многоугольник, и хотя квадрат представляет собой тип прямоугольника, прямоугольники, которые составляют , а не квадратов, не будут правильными многоугольниками.
Пример 2
Найдите сумму углов шестиугольника в градусах. Предполагая, что шестиугольник равен , обычный , найдите градус каждого внутреннего угла.
Что мы знаем?
Мы можем использовать формулу S = (x — 2) (180) для суммирования степени любого многоугольника.
У шестиугольника 6 сторон, поэтому x = 6.
Решить
Пусть x = 6 в формуле и упростит:
S = (6-2) (180)
S = 4 (180)
S = 720Правильный многоугольник — это равноугольный , что означает, что все углы имеют одинаковую величину.
 В случае правильного шестиугольника сумма в 720 градусов будет равномерно распределена между шестью сторонами.
В случае правильного шестиугольника сумма в 720 градусов будет равномерно распределена между шестью сторонами.Итак, 720/6 = 120. В правильном шестиугольнике шесть углов, каждый по 120 градусов.
Пример 3
Если сумма углов многоугольника равна 3600 градусам, найдите количество сторон многоугольника.
Изменение формулы на противоположное
Опять же, мы можем использовать формулу S = (x — 2) (180), но на этот раз мы решаем для x вместо S. Ничего страшного!
Решить
В этой задаче положим S = 3600 и решим относительно x.
3600 = (x — 2) (180)
3600 = 180x — 360
3600 + 360 = 180x
3960 = 180x
3960/180 = x
22 = xМногоугольник с 22 сторонами имеет 22 угла, сумма которых равна 3600 градусам.
Внешние углы многоугольника
В каждой вершине многоугольника может быть образован внешний угол путем удлинения одной стороны многоугольника, так что внутренний и внешний углы в этой вершине являются дополнительными (в сумме 180).
 На рисунке ниже углы a, b, c и d являются внешними, а сумма их градусов равна 360.
На рисунке ниже углы a, b, c и d являются внешними, а сумма их градусов равна 360.Если у правильного многоугольника x сторон, то каждый внешний угол равен 360, деленному на x.
Давайте рассмотрим два типовых вопроса.
Пример 4
Найдите градус каждого внутреннего и внешнего угла правильного шестиугольника.
Помните, что формула суммы внутренних углов S = (x-2) * 180. У шестиугольника 6 сторон. Поскольку x = 6, сумму S можно найти, используя S = (x — 2) (180)
S = (10-6) (180)
S = 4 (180)
S = 720В шестиугольнике шесть углов, а в правильном шестиугольнике все они равны.Каждый составляет 720/6 или 120 градусов. Теперь мы знаем, что внутренние и внешние углы составляют дополнительных (в сумме 180) в каждой вершине, поэтому размер каждого внешнего угла составляет 180 — 120 = 60.
Пример 5
Если размер каждого внутреннего угла правильного многоугольника равен 150, найдите количество сторон многоугольника.

Ранее мы определили количество сторон в многоугольнике, взяв сумму углов и используя формулу S = (x-2) * 180 для решения. Но на этот раз мы знаем только размер каждого внутреннего угла.Нам пришлось бы умножить на количество углов, чтобы найти сумму … но вся проблема в том, что мы еще не знаем количество сторон ИЛИ сумму!
Но, поскольку размер каждого внутреннего угла равен 150, мы также знаем, что мера внешнего угла, проведенного в любой вершине в терминах этого многоугольника, равна 180 — 150 = 30. Это потому, что они образуют дополнительные пары (внутренний + внешний = 180).
До примера 4 мы узнали, что также можем вычислить величину внешнего угла в правильном многоугольнике как 360 / x, где x — количество сторон.Теперь у нас есть способ найти ответ!
30 = 360 / x
30x = 360
x = 360/30
x = 12Наш многоугольник с внутренними углами 150 градусов (и внешними углами 30 градусов) имеет 12 сторон.
Кстати, геометрическая фигура с 12 сторонами называется двенадцатигранником.

Урок от г-на Фелиза
.
Инструменты «Многоугольник» и «Линия», построение звёзд и стрелок
Автор Дмитрий Евсеенков На чтение 6 мин Просмотров 1.4к. Обновлено
Ранее я рассказал о следующих векторных фигурах Photoshop:
? Прямоугольник (Rectangle Tool)
? Прямоугольник со скруглёнными углами (Rounded Rectangle
Tool)
? Эллипс (Ellipse Tool)Как совмещать и вычитать векторные фигуры в Photoshop, Вы можете узнать из этой статьи.
В этом уроке я расскажу двух о следующих инструментах этой группы — Многоугольник (Polygon Tool) и Линия (Line Tool).
Содержание
Инструмент Многоугольник (Polygon Tool)
Следующим после «Эллипса», в стеке векторных инструментов располагается «Многоугольник», с помощью которого можно получить весьма интересные фигуры:
Выбор инструмента «Многоугольник» Polygon Tool.

В то время как фигура, создаваемая при помощи инструмента «Прямоугольник», ограничена четырьмя углами, инструмент «Многоугольник» позволяет нам создавать фигуры многоугольной формы с числом углов от трёх и до ста. Кроме того, с помощью этого инструмента мы можем создавать фигуры в форме звезд. Чтобы нарисовать фигуру с помощью Polygon Tool, сначала введите нужное вам количество сторон в опцию «????Стороны» (Sides) на панели параметров. Как я упоминал выше, Вы можете ввести любое число от 3 ??до 100. Я оставлю значение по умолчанию 5:
Введите нужное вам число сторон в опцию «Стороны» (Sides) на панели параметров.
После того, как вы ввели число сторон, нажмите и перетащите курсор в документе. Photoshop всегда создаёт многоугольник от центра, так что нет необходимости удерживать клавишу Alt. Зажатая клавиша ??Shift после начала перетаскивания выравнивает фигуры с чётным количеством сторон:
Пятиугольник, построенный с помощью инструмента «Многоугольник» (Polygon Tool).

Установка числа сторон 3 в панели параметров дает нам простой способ создания треугольника:
Равносторонний треугольник, построенный с помощью инструмента «Многоугольник» (Polygon Tool).
А вот пример фигуры многоугольника с количеством сторон 12
Двенадцатиугольник, отображение контура отключено
Как и в случае с радиусом скруглений для инструмента «Прямоугольник со скруглёнными углами», Photoshop не позволяет изменить число сторон после создания фигуры, так что если перед началом построения фигуры вы неправильно указали количество сторон, остаётся только нажать Ctrl+Z для отмены шага по построению фигуры, а затем ввести другое значение в опцию «Стороны» (Sides) и начать рисовать многоугольник заново:
Рисование звезды с помощью «Многоугольника» (Polygon Tool)
Чтобы нарисовать звезду при помощи этого инструмента, нажмите на значок шестеренки в панели параметров, а затем выберите опцию «Звезда» (Star):
Нажатие на значок шестеренки и выбор опции «Звезда» (Star).

Затем просто нажмите внутри документа и создайте фигуру звезды методом перетаскивания курсора. При активной опции «Звезда» (Star), опция «Стороны» (Sides) в панели параметров задаёт количество лучей звезды. Так, при его значении 5 у нас получится пятиконечная звезда:
Пятиконечная звезда, начерченная с помощью инструмента «Многоугольник», параметры фигуры заданы по умолчанию.(Polygon Tool).
Изменение значения сторон на 8 дает нам восьмиконечную звезду:
Управление количеством лучей звезды.
Мы можем изменять у звездообразной фигуры не только количество лучей, но и положение внутренних вершин между центром звезды и внешними вершинами. По умолчанию, внутренние вершины находятся посередине, за это отвечает параметр «Глубина лучей» (Indent Sides By), по умолчанию он равен 50%:
Изменение параметра «Глубина лучей» (Indent Sides By) с 50 процентов, заданных по умолчанию, до 90%.
Посмотрите, что получилось:
Та же восьмиконечная звезда, но со значением параметра «Глубина лучей» (Indent Sides By) 90%.
 Контур скрыт.
Контур скрыт.По умолчанию, звезды имеют острые углы на вершинах, но мы можем сделать их закруглёнными, выбрав опцию «Сгладить внешние углы» (Smooth Corners):
Включение скругления углов при помощи опции «Сгладить внешние углы» (Smooth Corners).
Во как будет выглядеть стандартная пятиконечная звезда со сглаженными вершинами лучей при включенной опции «Сгладить внешние углы» (Smooth Corners):
Опция сглаживания углов придает звезде веселый, дружелюбный вид.
Мы можем сгладить не только вершины лучей, но и вершины впадин с помощью опции «Сгладить внутренние углы» (Smooth Indents):
Включение опции «Сгладить внутренние углы» (Smooth Indents).
При включении обеих этих опций мы получаем форму, похожую на морскую звезду:
Звезда с сглаженными углами и впадинами получена при одновременном включении опций «Сгладить внешние углы» (Smooth Corners) и «Сгладить внутренние углы» (Smooth Indents).
Инструмент Линия (Line Tool)
Последним из основных геометрических инструментов формы Photoshop является инструмент «Линия» (Line Tool).
 Я выберу его на панели инструментов:
Я выберу его на панели инструментов:Выбор инструмента «Линия» (Line Tool).
Инструмент «Линия» позволяет создавать простые прямые линии, но кроме этого мы можем использовать его для рисования фигур в виде стрелки. Чтобы нарисовать прямую линию, во-первых, установите толщину линии, которую следует задать в пикселях в поле ввода «Толщина» (Weight) в панели параметров. Значение по умолчанию задано в 1 пиксель. Я увеличу его до 16-ти пикселей:
Опция «Толщина» (Weight) задаёт толщину (ширину) линии.
Также, как и при работе другими инструментами векторных форм, для создания линии, нажмите левой клавишей мыши внутри документа и перетащите вашу линию. Чтобы проще было построить горизонтальную, вертикальную или линию под углом 45 градусов, зажмите клавишу ??Shift в процессе перетаскивания курсора, и отпустите клавишу Shift после отпускания клавиши мыши:
Держите клавишу Shift при перетаскивании курсора для создания горизонтальных или вертикальных линий.

Рисование указательных стрелок (стрелок направления)
Чтобы из линии получить стрелку, нажмите на значок шестеренки на панели параметров, чтобы открыть окно опции «Стрелки» (Arrowhead) с вариантами изменения наконечника (острия) стрелки. Выберите, чтобы наконечник отобразился в начале линии, в конце линии или же с обоих сторон сразу:
Нажмите на значок шестеренки для доступа к опции «Стрелки» (Arrowhead).
Вот линия, начерченная, как и ранее, но на этот раз со стрелкой на конце:
Инструмент «Линия» позволяет легко рисовать указательные стрелки, размеры наконечника стрелки заданы Photoshop по умолчанию.
Если размеры по умолчанию наконечника стрелки вам не подходят, вы можете настроить их, изменив параметры «Ширина» (Width) и «Длина» (Length).
«Ширина» и «Длина» наконечника задаются в процентах от толщины линии, значит, на данный момент ширина моего наконечника стрелки 80 пикселей, а длина -160.
Вы также можете заострить хвостовик наконечника путем увеличения параметра «Кривизна» (Concavity). Я повышу его значение с 0% по умолчанию до 50%:
Я повышу его значение с 0% по умолчанию до 50%:Опция «Кривизна» (Concavity) для изменения формы наконечника стрелы методом заострения его краев.
Вот так стрелка выглядит теперь. Перед тем, как начать рисовать фигуру, убедитесь, что вы правильно задали параметры инструмента «Линия», так как они не могут быть скорректированы после (если вам необходимо внести изменения, вам нужно отменить форму и рисовать новую).
Геометрия многоугольника: пятиугольники, шестиугольники и додекагоны
Немногие геометрические фигуры столь же разнообразны, как многоугольники. Они включают в себя знакомый треугольник, квадрат и пятиугольник, но это только начало.
В геометрии многоугольник — это любая двумерная форма, которая удовлетворяет следующим условиям:
- Состоит из трех или более прямых
- Закрыто без отверстий или разрывов в форме
- Имеет пары линий, которые соединяются в углах или вершинах, где они образуют углы
- Имеет равное количество сторон и внутренних углов
Двумерный означает плоский, как лист бумаги.
 Кубы не являются полигонами, потому что они трехмерны. Круги не являются полигонами, потому что они не содержат прямых линий.
Кубы не являются полигонами, потому что они трехмерны. Круги не являются полигонами, потому что они не содержат прямых линий.Специальный вид многоугольника может иметь углы, которые не все равны. В этом случае это называется неправильным многоугольником.
О полигонах
Де Агостини / А. Дагли Орти / Getty Images
Название многоугольника происходит от двух греческих слов:
- Поли , что означает много
- Гон , что означает угол
Формы, которые являются полигонами
- Треугольник (треугольник): 3 стороны
- Тетрагон (квадрат): 4 стороны
- Пентагоны: 5 сторон
- Шестиугольник: 6 сторон
- Семиугольник: 7 сторон
- Восьмиугольники: 8 сторон
- Нонагон: 9 сторон
- Декагон: 10 граней
- Undecagon: 11 сторон
- Додекагоны: 12 сторон
Как называются полигоны
Названия отдельных многоугольников получаются из числа сторон или углов, которыми обладает форма.
 Полигоны имеют одинаковое количество сторон и углов.
Полигоны имеют одинаковое количество сторон и углов. Общим названием большинства полигонов является греческий префикс «сторон», прикрепленный к греческому слову «угол» (gon).
Примеры этого для пяти- и шестигранных правильных многоугольников:
- Пента (по- гречески означает пять) + гон = пентагон
- Гекса (по-гречески означает шесть) + гон = шестиугольник
Есть исключения из этой схемы именования. В частности, со словами, которые чаще всего используются для некоторых полигонов:
- Треугольник: Использует греческий префикс Tri , но вместо греческого угольник , латинский угол используется. Trigon — правильное геометрическое имя, но оно используется редко.
- Четырехсторонний : Производный от латинского префикса quadri, означающего четыре, прикрепленного к слову боковой, что является еще одним латинским словом, означающим сторону .

- Квадрат : Иногда четырехсторонний многоугольник (квадрат) называют четырехугольником или четырехугольником .
N-угольники
Полигоны с более чем 10 сторонами встречаются нечасто, но следуют тому же греческому соглашению об именовании. Итак, 100-сторонний многоугольник называется гектогоном .
Однако в математике пятиугольники иногда более удобно называть n-гонами :
- 11-гонник: гендекагон
- 12-Гон: Додекагон
- 20-летний гонщик: Икосагон
- 50-гонник: пятиконечный
- 1000-гон: чилиагон
- 1000000-гон: мегагон
В математике н-гоны и их греческие аналоги взаимозаменяемы.
Предел полигона
Теоретически, нет ограничения на количество сторон, которые может иметь многоугольник.
По мере того, как размер внутренних углов многоугольника увеличивается, а длина его сторон становится короче, многоугольник приближается к кругу, но никогда не достигает его.

Классификация полигонов
Регулярные и неправильные полигоны
Полигоны классифицируются на основании того, равны ли все углы или стороны.
- Правильный многоугольник : все углы имеют одинаковый размер, и все стороны равны по длине.
- Нерегулярный многоугольник : Не имеет равных углов или сторон одинаковой длины.
Выпуклые против вогнутых полигонов
Второй способ классификации полигонов — по размеру их внутренних углов.
- Выпуклые многоугольники : не имеют внутренних углов больше 180 °.
- Вогнутые многоугольники : имеют как минимум один внутренний угол, превышающий 180 °.
Простые и сложные полигоны
Еще один способ классификации полигонов — это то, как линии, образующие многоугольник, пересекаются.
- Простые многоугольники : линии соединяются или пересекаются только один раз — в вершинах.

- Сложные полигоны : линии пересекаются более одного раза.
Названия сложных многоугольников иногда отличаются от названий простых многоугольников с одинаковым числом сторон.
Например:
- Регулярный образный шестигранник представляет собой шестигранный, простой многоугольник.
- Звездообразная гексаграмма представляет собой шестигранный сложный многоугольник, созданный путем наложения двух равносторонних треугольников.
Правило суммы внутренних углов
Ян Лишман / Getty Images
Как правило, каждый раз, когда сторона добавляется в многоугольник, например:
- От треугольника до четырехугольника (три-четыре стороны)
- От пятиугольника до шестиугольника (пять-шесть сторон)
еще 180 ° добавляется к сумме внутренних углов.
Это правило можно записать в виде формулы:
(n — 2) × 180 °
где n равно числу сторон многоугольника.

Таким образом, сумма внутренних углов для шестиугольника может быть найдена с помощью формулы:
(6 — 2) × 180 ° = 720 °
Сколько треугольников в этом многоугольнике?
Приведенная выше формула внутреннего угла получается путем деления многоугольника на треугольники, и это число можно найти с помощью вычисления:
п — 2
В этой формуле n равно числу сторон многоугольника.
Шестиугольник (шесть сторон) можно разделить на четыре треугольника (6-2) и додекагон на 10 треугольников (12-2).
Размер угла для правильных многоугольников
Для правильных многоугольников, в которых все углы одинакового размера, а стороны одинаковой длины, размер каждого угла в многоугольнике можно рассчитать путем деления общего размера углов (в градусах) на общее количество сторон.
Для правильного шестигранного шестигранника каждый угол равен:
720 ° ÷ 6 = 120 °
Некоторые известные полигоны
Скотт Каннингем / Getty Images
Хорошо известные полигоны включают в себя:
Фермы
Фермы часто имеют треугольную форму.
 В зависимости от ширины и уклона крыши ферма может включать равносторонние или равнобедренные треугольники. Из-за их большой прочности, треугольники используются в строительстве мостов и велосипедных рам. Они видны в Эйфелевой башне.
В зависимости от ширины и уклона крыши ферма может включать равносторонние или равнобедренные треугольники. Из-за их большой прочности, треугольники используются в строительстве мостов и велосипедных рам. Они видны в Эйфелевой башне.Пентагон
Пентагон — штаб-квартира Министерства обороны США — берет свое название от его формы. Здание представляет собой пятисторонний, правильный пятиугольник.
Главная пластина
Другой известный пятисторонний правильный пятиугольник — домашняя тарелка на бейсбольном алмазе.
Поддельный Пентагон
Гигантский торговый центр недалеко от Шанхая, Китай, построен в форме правильного пятиугольника и иногда называется поддельным пятиугольником.
Снежинки
Каждая снежинка начинается с шестиугольника, но температура и влажность добавляют ветви и усики, так что каждая из них выглядит по-разному.
Пчелы и осы
Естественные шестиугольники также включают ульи, где каждая клетка в соте, которую пчелы строят для содержания меда, является шестиугольной.
 Гнезда бумажных ос также содержат гексагональные клетки, в которых они растут.
Гнезда бумажных ос также содержат гексагональные клетки, в которых они растут.Тротуар гиганта
Шестиугольники также найдены на мощёной дорожке Гиганта, расположенной на северо-востоке Ирландии. Это естественная горная порода, состоящая из около 40000 взаимосвязанных базальтовых колонн, которые были созданы в виде лавы от медленно вулканического извержения вулкана.
Восьмиугольник
Восьмиугольник — имя, данное кольцу или клетке, используемому в боях Ultimate Fighting Championship (UFC), — берет свое название от своей формы. Это восьмигранный правильный восьмиугольник.
Стоп Знаки
Стоп-знак — один из самых знакомых дорожных знаков — еще один восьмигранный правильный восьмиугольник. Хотя цвет, формулировка или символы на знаке могут отличаться, восьмиугольная форма знака остановки используется во многих странах мира.
Многоугольные рамки для фото и картин
Многоугольные — в этой статье рассмотрим вопрос изготовления рамок, которые в некотором роде связаны с многоугольными формами.
 Лучше всего начать с того, что нужно вспомнить из далекой начальной школы, что такое многоугольник.
Лучше всего начать с того, что нужно вспомнить из далекой начальной школы, что такое многоугольник.Многоугольные и математика для них
- Плоские замкнутые ломаные линии — общий случай;
- Плоские замкнутые ломаные линии без самопересечений — простые многоугольные;
- Часть плоскости, ограниченная замкнутыми ломаными линиями без самопересечений.
На рисунке ниже: (а) пятиугольник; (b) шестиугольник; (c) не является многоугольником, потому что он не замкнут; (d) не является многоугольником, потому что есть линии самопересечений; и (e) не является многоугольные, так как не все его линии являются прямыми. Виды многоугольников, с разным числом ребер и их имена показаны на рисунке ниже.
Многоугольные формы
Обычные многоугольники имеют свойство, они находятся в кругу, который называется окружностью и соприкасается со всеми вершинами многоугольника. Центром правильного многоугольника всегда является центр его круга.
Допустим, что наш многоугольник имеет количество углов = N, круг имеет всегда 3600 и градус угла определяем из формулы 3600/N.

Например, шестиугольник имеет N=6 углов и образует угол в центре круга равный 3600/6 = 600.
Внутренние углы нашего многоугольника одинаковы и равны 1800( N-2 )/N градусов.
Например, внутренние углы квадрата равны 1800( 4-2 )/4 = 900; у восьмиугольника 1800( 8-2 )/8 = 1350.
По мере увеличения числа ребер в многоугольнике, длина ребра будет уменьшаться и в конечном итоге они сойдутся в одну окружность.
Некоторые изделия, имеющие многоугольную форму, без изменения размеров сторон показаны на рисунке ниже. Шкатулка имеет форму восьмиугольника, рамки для зеркала, которые имеют прямоугольную и шестиугольную формы. Разделочная доска, не правильный многоугольник, он состоит из двух форм, квадрата и восьмиугольника. Некоторые изделия, имеющие многоугольную форму, с изменением размеров сторон показаны на рисунке ниже. Ваза имеет семь сторон с наклоном в наружу, то есть снизу вверх, настольная лампа, наоборот, имеет наклон во внутрь с шестью сторонами.

Дальше рассмотрим ряд некоторых математических аспектов для многоугольников, которые нужны при расчете многоугольных изделий.Равносторонний многоугольник.
Главными переменными на многоугольные формы есть внутренние углы, длина ребер, и площадь изделия. Как видно из рисунка сегмент N-углов вписан в две окружности, обозначим их, как внутренний и внешний круг. Обозначим три стороны треугольника (стороны R, r, и l) его стороны образованы радиусами и ребром, обозначим три угла, которые расположены в треугольнике (А1, А2 и А3). Между концами этих радиусов внутри двух кругов проведем линию с одной конечной точкой в месте касания к внутреннему кругу и другой точкой в месте касания к внешнему кругу. Радиус — отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка R. Радиус составляет половину диаметра 2R.
Угол A1 составляет половину центрального угла и равен 1800/N для N-углов.
 Угол А2 = 900, потому что радиус круга (r) касается к сегменту (l) под прямым углом.
Угол А2 = 900, потому что радиус круга (r) касается к сегменту (l) под прямым углом.Это означает, что угол А3 и радиус (R) есть составляющие угла А1 и поэтому А3=900-А1=900(N-2)/N. который является половиной внутреннего угла.
Две стороны определяют третью сторону треугольника, потому что R2=r2+l2. Определим стороны r и l по отношению к углу А1: r=Rcos А1 и l=Rsin А1.
Определим длину ребра L: L=2l=2Rsin А1, это формулы определения градусов в N-углах.
.
Пример: Рассмотрим пятиугольник имеющий длину стороны L=1 дюйм. Угол А1=1800/5=360, угол А2=900-360=540.
Пятиугольник лежит внутри окружность радиуса R=L/(2sin А1)=1/(2sin 360)=0,85 дюйма.
Пример: Рассмотрим шестиугольник, внутренний круг, имеет диаметр 1,7 дюйма.
 Определяем радиус окружности R=1,7/2=0,85 дюйма. Угол А1=1800/6=300 и угол А3=600. Длина ребра равна L=2Rsin=1.7sin300=0,85 дюйма.
Определяем радиус окружности R=1,7/2=0,85 дюйма. Угол А1=1800/6=300 и угол А3=600. Длина ребра равна L=2Rsin=1.7sin300=0,85 дюйма.Углы А1 и А3 важны в создании формы правильного многоугольника и они отмечены в таблице для:
квадрата, пятиугольника, шестиугольника, восьмиугольника.
Разносторонние многоугольные.N углов центральный угол внутренний угол A1 A3 4 90 90 45 45 5 72 108 36 54 6 60 120 30 60 8 45 135 22,5 67,5 Разносторонние многоугольники — те, которые имеют стороны не равной длины. Примеры угловых шкафов на рисунке ниже.
 Здесь углы и ребра разной длины и зависят от конкретных условий.
Здесь углы и ребра разной длины и зависят от конкретных условий.Те, кому интересна тригонометрия, формулы и примеры:
http://dls-website.com/documents/WoodworkingNotes/Compound%20Miters.pdf http://www.woodcentral.com/bparticles/miter_formula.shtml http://www.woodworkersguildofga.org/ShopHelpers/CompoundMiterTable.pdf Также существует программа написанная на языке Frink, которая позволяет делать расчеты для углов многоугольников на настольных компьютерах и смартфонах, Android-ах и iPhon-ах, она работает с компьютерами на платформе Андроид. Frink — компьютерный язык-программирования, на котором написана программа. Сама программа расположена по адресу: http://dls-website.com/documents/WoodworkingNotes/Compound%20Miters.pdf, там же описание программы и ее настройки. Инструкции по использованию языка-программирования можно получить бесплатно с сайтов: https://play.google.com/store/search?q=Frink+programming+language&c=apps и http://futureboy.us/frinkdocs/frinkframe.
 html . Один из способов реализовать использование языка-программирования Фринк, это загрузить его в настольный компьютер, который будет использоваться. После того как приложение заработает в среде рабочего стола, его можно будет отправить в сотовый телефон по проводному или беспроводному соединению. После загрузки в телефон, «приложение» может быть использовано там, как калькулятор. Онлайн калькуляторов расчета углов, для многоугольников,в интернете тоже предостаточно:
html . Один из способов реализовать использование языка-программирования Фринк, это загрузить его в настольный компьютер, который будет использоваться. После того как приложение заработает в среде рабочего стола, его можно будет отправить в сотовый телефон по проводному или беспроводному соединению. После загрузки в телефон, «приложение» может быть использовано там, как калькулятор. Онлайн калькуляторов расчета углов, для многоугольников,в интернете тоже предостаточно:
http://www.woodworkersguildofga.org/ShopHelpers/MiterCalculator.htm
http://jansson.us/jcompound.html
http://www.pdxtex.com/canoe/compound.htmТорцовочное приспособление на многоугольные. Торцовочное приспособление необходимо в различных проектах многоугольников, имеющих наклонные стороны. Ниже на рисунке показаны два необходимых реза под углом на циркулярном станке. Один из них создает углы торцов изделия, которые соединяют стороны многоугольника между собой, а другой рез создает углы наклона во внутрь или в наружу для каждой стороны, смотрите рисунок ниже.

Многогранники
Многоугольники являются двухмерными изделиями. Закрытые трехмерные изделия могут быть изготовлены из них путем присоединения многоугольников вдоль их краев. Объекты, полученные таким образом, называются многогранники. Куб полученный соединением шести квадратов является примером многогранника. Другим примером является додекаэдр, он показаны на рисунке слева и на рисунке ниже: (а) античная многогранная шкатулка; (б) додекаэдрическая система динамиков; (с) додекаэдрические солнечные часы, они построены из двенадцати одинаковых пятиугольников. Каждая пятиугольная грань составляет 0,5 дюйма толщиной красного дерева с использованием шаблона метод резки на рисунке ниже.
Важное значение в построении многогранников имеют скошенные уголки его многоугольных граней, детальнее: http://dls-website.com/documents/PolyhedralSundials.pdf
Метки: как сделать рамку для картины, красивые рамки для фото, рамка для фото, рамки для картин, рамки для картин своими руками, рамки для фото своими руками.
 Закладка Постоянная ссылка.
Закладка Постоянная ссылка.Five Sided Shape — Bilder und Stockfotos
14.938Bilder
- Bilder
- Fotos
- Grafiken
- Vektoren
- Videos
Niedrigster Preis
SignatureBeste Qualität
Durchstöbern Sie 14.938
five sided shape Фото и фотографии. Oder starten Sie eine neuesuche, um noch mehr Stock-Photografie und Bilder zu entdecken. fünfeck, sechseck, achteck-символ. вектор-геометрия-многоугольник. — пятисторонняя форма — графика, -клипарт, -мультфильмы и -символФюнфек, Сехсек, Ахтек-Символ. Вектор-Геометрия-Полигон.
das pentagon-luftbild — пятисторонняя форма стоковые фотографии и изображенияDas Pentagon-Luftbild
abstrakte bunte mosaik blumenmuster symbol knöpfe sammlung — пятисторонняя форма stock-grafiken, -clipart, -cartoons und -symboleAbstrakte bunte Symbol Knöpöpöpmuster Sammlung
bunte aquarell векторные украшения rahmen und luftballons; рейтинг, инфографика — пятисторонняя форма, графика, -клипарт, -мультфильмы и -символbunte Aquarell Vector Dekoration Rahmen und Luftballons; Рейтинг,
векторных иллюстраций пятиугольной системы с градиентной головкой. — пятисторонняя форма — графика, -клипарт, -мультфильмы и -символ
— пятисторонняя форма — графика, -клипарт, -мультфильмы и -символВекторная иллюстрация Pentagon Systeme Gradient bunt.
Weiße тоннель, коридор — пятисторонняя форма сток-фотографии и изображения , -мультики и -символQuadratische sfünfeckige und sechseckige Infografik (Teil vier,…
Pentagon-logo bunte schnitttafeln, die teamwork, kommunikation oder allianz symbolisieren — пятисторонняя форма, графика, -клипарт, -мультфильмы и -символPentagon-Logo bunte, Schnitttafeln die Командная работа, Коммуникация…
вектор-инфографика дизайн-ворлаж.- пятисторонняя форма-графика,-клипарт,-мультфильмы и-символвектор-инфографика-дизайн-слово. графика, -клипарт, -мультфильмы и -символ
Geometrische Formen-Symbole
Geometrische Formen Symbole , Vektorillustration
Коллекция 22 треугольных геометрических иконок im verlaufslinienstil — пятисторонняя форма stock-grafiken, -clipart, -cartoons und -symbole , sechseck, семиугольник, achteck для инфографики. — пятисторонняя графика, -клипарт, -мультфильмы и -символы
— пятисторонняя графика, -клипарт, -мультфильмы и -символыDreieck, Quadrat, Fünfeck, Sechseck, Heptagon, Achteck für…
Dreieck, Quadrat, Fünfeck, Sechseck, Heptagon, Achteck für Infografiken mit kreisförmigen Pfeilen Vector-Designelemente
Glassmorphism fünfeck infografik konzept mit 3d geometrischen formen. эффект матового стекла. abbildung auf verschwommenem farbverlaufsvektorhintergrund — пятисторонняя графика формы, -клипарт, -мультфильмы и -symboleGlassmorphism Infeck Infografik Konzept mit 3D geometrischen…
vector pentagon-infografik mit 5 optionen. презентацииrutsche. — пятисторонняя форма — графика, -клипарт, -мультфильмы и -символВекторная инфографика Пентагона с 5 вариантами. Презентации.
Абстрактная мозаика Schneeflocke Набор иконок для дизайна — пятисторонняя форма, графика, клипарт, мультфильмы и символыАбстрактная мозаика Schneeflocke Набор иконок Набор для дизайна
бизнес-информация. диаграмма с 3, 4, 5, 6, 7, 8 начертано, опционально, отпущено. векторворлаге. — пятисторонняя форма сток-графика, -клипарт, -мультфильмы и -символ
диаграмма с 3, 4, 5, 6, 7, 8 начертано, опционально, отпущено. векторворлаге. — пятисторонняя форма сток-графика, -клипарт, -мультфильмы и -символБизнес-инфографика. Схема с 3, 4, 5, 6, 7, 8 схемами,…
infografik-designvorlage mit platz für ihre daten. вектор-иллюстрация. — пятисторонняя форма — графика, -клипарт, -мультфильмы и -символыInfografik-Designvorlage mit Platz für Ihre Daten. Vektor-Illustra
Infografik-Design-Vorlage mit Platz für Ihren Text. Векториллюстрация.
геометрическая структура текстуры с молекулярной структурой и химической инженерией. zusammenfassung hintergrund der sechsecke muster. — пятисторонняя форма — графика, -клипарт, -мультфильмы и -символGeometrische Hintergrundtextur mit Molekularen Strukturen und…
абстрактный технологический туннель — пятисторонняя форма, фото и изображенияабстрактный технологический туннель
бизнес-инфографика, диаграмма, опциональное представление 5 — пятисторонняя форма, графика, клипарт, мультфильмы и -symboleBusiness infographic, Diagramm, Optionen Präsentation 5
luftaufnahme des pentagons usa, us-verteidigungsministerium hauptsitz in arlington, virginia, in der nähe von Washington, dc, mit 395 шоссе и мемориал военно-воздушным силам и арлингтонское кладбище в дер-Нээ. — пятисторонние фото и изображения
— пятисторонние фото и изображенияLuftaufnahme des Pentagons USA, US-Verteidigungsministerium…
pentagon-vogelauge — пятисторонние изображения и изображенияPentagon-Vogelauge
bunte geometrie-musterhintergrund — пятисторонние изображения графика, клипарт, мультфильмы и символыBunte Geometrie-Muster Hintergrund
векторная геометрическая информация. vorlage für циклическая диаграмма, диаграмма, презентация и — пятисторонняя форма — графика, -клипарт, -мультфильмы и -символВекторная геометрическая инфографика. Описание цикла Diagramm,…
Макет для Ihre Optionen oder Schritte. Abstrakte Vorlage für den Hintergrund.
Pentagon Padlock Security Concept Illustration — пятисторонняя форма стоковые фото и иллюстрацииPentagon Padlock Security Defense Concept Illustration -symbole
Satz von bunten Mosaik Floral Muster Knöpfe Icon-Kollektion für…
пятиугольник-символ — пятисторонняя форма сток-графика, -клипарт, -мультфильмы и -символпятиугольник-символ
вектор-крайняя инфографика. vorlage für диаграмма цикла, диаграмма, презентация — пятисторонняя форма, графика, -клипарт, -мультфильмы и -символы
vorlage für диаграмма цикла, диаграмма, презентация — пятисторонняя форма, графика, -клипарт, -мультфильмы и -символыVektor-Kreis Pfeile Infografik. Описание цикла Diagramm,…
двойных золотых изображений с изображением векторной иллюстрации. реалистичная трехмерная элегантная золотая награда с блеском, классическая геометрическая презентация, малрахмен изолирован на прозрачном фоне. — пятисторонняя форма — графика, -клипарт, -мультфильмы и -символЗолотистый двойник Rahmen mit fünfeckiger Vektorillustration….
Золотистый двойник Rahmen mit fünfeckiger Formvektorillustration. Реалистичная трехмерная элегантная золотая награда с блестками, классическая геометрическая презентация, лакиеррахмен, изолированный на прозрачном фоне Hintergrund
design-elemente/pentagon — пятисторонняя форма, графика, клипарт, мультфильмы и символыDesign-Elemente/PENTAGON
американский город антенна / министерство обороны (пятиугольник) — пятисторонняя форма, фото и изображенияAmerican City Aerial / Министерство обороны (Пентагон)
Luftaufnahme des Verteidigungsministeriums, dem Eckpfeiler der Verteidigung der Vereinigten Staaten.
fünf teile puzzlepuzzle pentagon info grafik. — пятисторонняя форма — графика, -клипарт, -мультфильмы и -символы
Fünf Teile Puzzlepuzzle Pentagon Информация Графика.
Fünfteiliges Puzzle-Fünfeck-Diagramm. Pentagons Geschäftspräsentation Infografik. 5 Schritte, Teile, Teile des Prozessdiagramms. Abschnitt Vergleichen Banner. Инфографика головоломки. Маркетинговая стратегия.
Bunter Mobius-Streifen — пятисторонняя форма, графика, -клипарт, -мультфильмы и -символыBunter Mobius-Streifen
Векторзац фон Мобиуса-Страйфена, такие как Dreieck, Quadrat, Fünfeck и Sechseck gefaltet sind.
Американская патриотическая гниль, weiß und blau, hauptstadt, weißes haus und pentagon logos isoliert vektor illustration — пятисторонняя форма, графика, клипарт, мультфильмы и символыАмериканская патриотическая гниль, weiß und blau, Hauptstadt, Weißes
rotierendes fünfeckmuster — пятисторонняя графика, -клипарт, -мультфильмы и -символыRotierendes Fünfeckmuster
platonischen einfarbig — пятисторонняя форма, графика, -клипарт, -мультфильмы и -символы пятисторонняя форма — графика, -клипарт, -мультфильмы и -символAbstrakter Hintergrund des Sechseckmusters
пятиугольная форма fraktal gestaltung inmitten ecke — пятисторонняя форма, стоковые фотографии и изображенияPentagon Form Fraktal Gestaltung inmitten Ecke
abstraktes Konzeptdesign aus Pentagon, das ein fraktales Design aus der Ecke erstellt, das durch Überlappung überlappt wird in schwarzem isoliertem Hintergrund mit weichem Schatten, Gruppenformen auf der rechten und linken Seite der Ecken geschichtetes Bild bereit zum Drucken für Karten, Einladung, Designdruck
Circle Five Thema Infografik Design — пятисторонняя форма, графика, -клипарт, -мультфильмы и -символCircle Five Thema Infografik Design
Диамант Эдельштейн Линия Эдельштейна символ вектор-набор — пятисторонняя форма сток-графика, -клипарт, -мультфильмы и -символДиамант Эдельштейн Линия Эдельштейн Символ вектор-набор
Алмазная огранка тонкая линия набор иконок.
бизнес-информация. диаграмма с 3, 4, 5, 6, 7, 8 начертано, опционально, отпущено. векторворлаге. — пятисторонняя форма — графика, -клипарт, -мультфильмы и -символ Edelsteinsammlung von einfachen Umrissschildern. Juwelensymbol im linearen Stil. Кристалл, Эдельштейн schwarze Kontur Icons Design. Isoliert auf weißem Konzeptvektor Illustration
Edelsteinsammlung von einfachen Umrissschildern. Juwelensymbol im linearen Stil. Кристалл, Эдельштейн schwarze Kontur Icons Design. Isoliert auf weißem Konzeptvektor IllustrationБизнес-Инфографикен. Diagramme mit 3, 4, 5, 6, 7, 8 Schritten,…
5 fünfecken machen 1-Stern-symbol — пятисторонняя форма, графика, -клипарт, -мультфильмы и -символ5 Fünfecken machen 1-Stern -Symbol
3D абстрактное изображение с небольшим фоном, минимальное изображение дизайна — пятисторонняя форма, фото и изображения3D абстрактное изображение с небольшим фоном, минимальное…
3D-рендеринг Хинтергрунд. Leerer Rahmen für Text, Werbung. Минималес Weihnachtskonzept.
Fünfeckige Radarvorlage Spinnennetz Diagramm Spinne, 5S leere pentagon Radar Karte vorlage — пятисторонняя форма фондовая графика, -клипарт, -мультфильмы и -символы или футбольный мяч. schwarz-weiß geometrischehintergrund aus sich wiederholenden fünfecken. вектор — пятисторонняя форма сток-графика, -клипарт, -мультфильмы и -символ
schwarz-weiß geometrischehintergrund aus sich wiederholenden fünfecken. вектор — пятисторонняя форма сток-графика, -клипарт, -мультфильмы и -символМонохромный мяч nahtlose Сбор для спортивного футбольного мяча или футбольного мяча
Monochromes kugelnahtloses Сбор для спортивного футбола или футбольного мяча. Schwarz-weißer geometrischer Hintergrund aus Fünfecken. Vektor
big data infografik-design — пятисторонняя форма стоковая графика, -клипарт, -мультфильмы и -символBig Data Infografik-Design
пятиугольник 11 сентября мемориал — пятисторонняя форма стоковые фотографии и изображенияPentagon 11 сентября Memorial
logo des fotografen oder fotostudios, schwarz-weiß verschachtelte linien öffnung der kameralinse abstrakte sfünfeckzeichen — пятисторонняя форма, графика, -клипарт, -мультфильмы и -символLogo des Fotografen oder Fotostudios, schwarz-weiß…
векторный элемент для инфографики. — пятисторонняя форма — графика, -клипарт, -мультфильмы и -символВектор-Элемент для Infografik.
векторный элемент для инфографики. — пятисторонняя форма — графика, -клипарт, -мультфильмы и -символы
Элемент вектора Kreis для Infografik.
Fünf optionen Pentagon diavorlage — пятисторонняя форма, графика, -клипарт, -мультфильмы и -символыFünf Optionen Pentagon Diavorlage
Fünf-Optionen-Pentagon-Prozessdiagramm. Geschäftsdaten. Графика, Диаграмма. Kreatives Konzept für Infografik, Templates, Präsentation. Kann für Themen wie Planung, Teamarbeit verwendet werden.
Goldener Fünfeckrahmen für bild auf schwarzem Hintergrund. leerraum für bild, malerei, karte oder foto. Трехмерная реалистичная современная векторная иллюстрация. einfaches goldes objektmodell — пятисторонняя форма, графика, клипарт, мультфильмы и символыGoldener Fünfeckrahmen für Bild auf schwarzem Hintergrund….
3D-рендеринг черных неоновых фонарей формы с блестящими ручками и размытым фоном — пятисторонняя форма стоковых фотографий и изображений -clipart, -cartoons und -symboleГеометрический дизайн логотипа
vektorillustration der malbuchseite für kinder mit umrissener Clipart zum ausmalen. buchstabe p für pentagon. — пятисторонняя форма — графика, -клипарт, -мультфильмы и -символ
buchstabe p für pentagon. — пятисторонняя форма — графика, -клипарт, -мультфильмы и -символVektorillustration der Malbuchseite für Kinder mit umrissener…
Pentagon-icon set — пятисторонняя форма, графика, -clipart, -cartoons und -symbolePentagon-icon-set
Pentagon Icon gesetzt. Векторгеометрия 5 Полигон-Лого.
sammlung von heiligengeometriessymbolen — пятисторонняя форма, графика, клипарт, мультфильмы и символы0002 konstruierte Architektur, Innenhof in Form eines Fünfecks элементы дизайна/наборы штрихов — пятисторонняя форма, графика, клипарты, мультфильмы и символы (новый современный элемент жестов). геометрическая структура текстуры с молекулярной структурой и химической инженерией. zusammenfassung hintergrund der sechsecke muster. — пятисторонняя форма — графика, -клипарт, -мультфильмы и -символGeometrische Hintergrundtextur с молекулярной структурой и…
Geometrische Hintergrundtextur с молекулярной структурой и Chemieingenieurwesen.
из 100. Abstrakter Hintergrund де Hexagonmusters. Векторная иллюстрация для медицинских и современных технологий. Дизайн
Abstrakter Hintergrund де Hexagonmusters. Векторная иллюстрация для медицинских и современных технологий. ДизайнПятисторонние фотографии и изображения
- CREATIVE
- РЕДАКЦИОННЫЕ
- ВИДЕО
- Beste Übereinstimmung
- Neuestes
- Ältestes
- Am beliebtesten
Alle Zeiträume24 Stunden48 Stunden72 Stunden7 Tage30 Tage12 MonateAngepasster Zeitraum
- Lizenzfrei
- Lizenzpflichtig
- RF und RM
Lizenzfreie Kollektionen auswählen >Editorial-Kollektionen auswählen >
Bilder zum Einbetten
Durchstöbern Sie 2.
 175 пятисторонняя форма Stock-Photografie und Bilder. Oder starten Sie eine neuesuche, um noch mehr Stock-Photografie und Bilder zu entdecken. Пентагон, Вашингтон, округ Колумбия, США — пятисторонняя форма стоковые фотографии и двусторонний вид Пентагона в Вирджинии -symbolegeometrische formen-symbole — пятисторонняя форма стоковой графики, -clipart, -cartoons und -symbolerotierendes fünfeckmuster — пятисторонняя форма stock-grafiken, -clipart, -cartoons и -symboleabstact пятиугольные художественные узоры — пятисторонняя форма stock-fotos und bilderSmoke И пламя поднимается над Пентагоном около 10 утра. Ориентировочное время: 11 сентября 2001 г. После предполагаемой террористической аварии угнанного коммерческого объекта… символ пятиугольника с инфографикой — пятисторонняя форма, графика, клипарт, карикатуры и символическая мозаика ртути — пятисторонняя форма. mosaik blumenmuster symbol knöpfe sammlung — пятисторонняя форма сток-графика, -клипарт, -мультфильмы и -символбакибол, молекула бакминстерфуллерена — пятисторонняя форма сток-графика, -клипарт, -мультфильмы и -символостральский вонючий гриб — пятисторонняя форма сток-фотографии и bilderdesign-elemente/streifen-set — пятисторонняя форма сток-графика, -клипарт, -мультфильмы и -символы профиль людей — пятисторонняя форма сток-графика, -клипарт, -мультфильмы и -символ абстракция графика-дизайн многоугольник пятиугольник обложка макет-ворладж — пятисторонняя графика, -клипарт, -мультфильмы и -символы, минимальная графика, дизайн, фон, абстрактный плакат — пятисторонняя графика, -клипарт, -мультфильмы и -символ Unte geometrie-muster hintergrund — пятисторонняя форма, графика, -clipart, -cartoons und -symboleabstrakte mosaik schneeflocke, набор иконок для дизайна — пятисторонняя форма, графика, -clipart, -cartoons und -symboledesign-elemente/streifen-symbole #4 — Пятисторонняя форма, графика, клипарт, мультфильмы и символы пятиугольника в Вашингтоне, округ Колумбия, США.
175 пятисторонняя форма Stock-Photografie und Bilder. Oder starten Sie eine neuesuche, um noch mehr Stock-Photografie und Bilder zu entdecken. Пентагон, Вашингтон, округ Колумбия, США — пятисторонняя форма стоковые фотографии и двусторонний вид Пентагона в Вирджинии -symbolegeometrische formen-symbole — пятисторонняя форма стоковой графики, -clipart, -cartoons und -symbolerotierendes fünfeckmuster — пятисторонняя форма stock-grafiken, -clipart, -cartoons и -symboleabstact пятиугольные художественные узоры — пятисторонняя форма stock-fotos und bilderSmoke И пламя поднимается над Пентагоном около 10 утра. Ориентировочное время: 11 сентября 2001 г. После предполагаемой террористической аварии угнанного коммерческого объекта… символ пятиугольника с инфографикой — пятисторонняя форма, графика, клипарт, карикатуры и символическая мозаика ртути — пятисторонняя форма. mosaik blumenmuster symbol knöpfe sammlung — пятисторонняя форма сток-графика, -клипарт, -мультфильмы и -символбакибол, молекула бакминстерфуллерена — пятисторонняя форма сток-графика, -клипарт, -мультфильмы и -символостральский вонючий гриб — пятисторонняя форма сток-фотографии и bilderdesign-elemente/streifen-set — пятисторонняя форма сток-графика, -клипарт, -мультфильмы и -символы профиль людей — пятисторонняя форма сток-графика, -клипарт, -мультфильмы и -символ абстракция графика-дизайн многоугольник пятиугольник обложка макет-ворладж — пятисторонняя графика, -клипарт, -мультфильмы и -символы, минимальная графика, дизайн, фон, абстрактный плакат — пятисторонняя графика, -клипарт, -мультфильмы и -символ Unte geometrie-muster hintergrund — пятисторонняя форма, графика, -clipart, -cartoons und -symboleabstrakte mosaik schneeflocke, набор иконок для дизайна — пятисторонняя форма, графика, -clipart, -cartoons und -symboledesign-elemente/streifen-symbole #4 — Пятисторонняя форма, графика, клипарт, мультфильмы и символы пятиугольника в Вашингтоне, округ Колумбия, США. — пятисторонние стоковые фотографии и картинки с изображениями — пятисторонние стоковые графики, -клипарты, -мультфильмы и -символы, детали из 9/ 11 мемориал в Нью-Йорке — пятисторонняя форма стоковые фотографии и изображения из мозаики цветочный набор knöpfe коллекция иконок для дизайна — пятисторонняя форма стоковая графика, -клипарт, -мультфильмы и -symboleabstrakter Hintergrund des sechseckmusters — пятисторонняя форма набор -grafiken, -clipart, -cartoons und -symboledas Elegante, geometrische design frame-lange schatten weichem defocushintergrund — пятисторонняя форма, -cartoons und -symbolehouse с узором калейдоскопа дымохода — пятисторонняя форма, stock-fotos und двухстороннее бетонное покрытие в форме пятиугольника и шестиугольника на пешеходной дорожке — пятисторонняя форма стоковые фотографии и минималистичный графический дизайн фоновый рисунок абстрактный плакат — пятисторонняя форма стоковая графика, -клипарт, -мультфильмы и -символДым поднимается из Пентагона после террористической атаки Сентябрь 11 сентября 2001 г.
— пятисторонние стоковые фотографии и картинки с изображениями — пятисторонние стоковые графики, -клипарты, -мультфильмы и -символы, детали из 9/ 11 мемориал в Нью-Йорке — пятисторонняя форма стоковые фотографии и изображения из мозаики цветочный набор knöpfe коллекция иконок для дизайна — пятисторонняя форма стоковая графика, -клипарт, -мультфильмы и -symboleabstrakter Hintergrund des sechseckmusters — пятисторонняя форма набор -grafiken, -clipart, -cartoons und -symboledas Elegante, geometrische design frame-lange schatten weichem defocushintergrund — пятисторонняя форма, -cartoons und -symbolehouse с узором калейдоскопа дымохода — пятисторонняя форма, stock-fotos und двухстороннее бетонное покрытие в форме пятиугольника и шестиугольника на пешеходной дорожке — пятисторонняя форма стоковые фотографии и минималистичный графический дизайн фоновый рисунок абстрактный плакат — пятисторонняя форма стоковая графика, -клипарт, -мультфильмы и -символДым поднимается из Пентагона после террористической атаки Сентябрь 11 сентября 2001 г. В Вашингтоне, округ Колумбия (на спутниковом снимке Пентагона ВМС США видны значительные повреждения западной стороны и внутренних колец многокольцевой здание в 11:46 утра по восточному поясному времени … набор элементов дизайна / круга № 3 — набор пятисторонних фигур на складе, — клипарт, — мультфильмы и -символы. клипарт, -мультфильмы и -symbolebunte геометрия собрать фоновую иллюстрацию — пятисторонняя форма сток-графика, -клипарт, -мультфильмы и -символкрупный план разноцветных шестиугольников, установленных на стене mehrere fünfecke mit abgerundeten ecken — пятисторонняя форма, -графика, -мультфильмы и -символы, минималистский дизайн обложки — пятисторонняя форма, -графика, -клипарт, -мультфильмы и -symboleabstrakte geometrische kreisförmige farbige pfade rahmen — пятисторонняя форма, набор -графики, -клипарты, -мультфильмы и -символыцифровые узоры — пятисторонние фото и изображения крупного плана вареной бамии, приправленные кацуобуси — пятисторонние изображения и изображения Пентагон, Вашингтон, округ Колумбия, Америка.
В Вашингтоне, округ Колумбия (на спутниковом снимке Пентагона ВМС США видны значительные повреждения западной стороны и внутренних колец многокольцевой здание в 11:46 утра по восточному поясному времени … набор элементов дизайна / круга № 3 — набор пятисторонних фигур на складе, — клипарт, — мультфильмы и -символы. клипарт, -мультфильмы и -symbolebunte геометрия собрать фоновую иллюстрацию — пятисторонняя форма сток-графика, -клипарт, -мультфильмы и -символкрупный план разноцветных шестиугольников, установленных на стене mehrere fünfecke mit abgerundeten ecken — пятисторонняя форма, -графика, -мультфильмы и -символы, минималистский дизайн обложки — пятисторонняя форма, -графика, -клипарт, -мультфильмы и -symboleabstrakte geometrische kreisförmige farbige pfade rahmen — пятисторонняя форма, набор -графики, -клипарты, -мультфильмы и -символыцифровые узоры — пятисторонние фото и изображения крупного плана вареной бамии, приправленные кацуобуси — пятисторонние изображения и изображения Пентагон, Вашингтон, округ Колумбия, Америка. 3D-вектор — пятисторонняя форма сток-графика, -клипарт, -мультфильмы и -символизируйте zitat rahmen leere vorlagen gesetzt. текст в klammern, zitat leere sprechblasen, zitat blasen. textbox isoliert auf pastellfarben hintergrund. — пятисторонняя графика формы, -клипарт, -мультфильмы и -символические абстрактные изображения — пятисторонняя графика формы, -клипарт, -мультфильмы и -символы, элегантные изображения для бизнес-берихта на многоугольнике внутри — пятисторонняя графика формы , -clipart, -cartoons und -symbolegrafik-informationen — пятисторонняя форма, -графика, -clipart, -cartoons und -symboleabstrakte mosaik schneeflocken, собрать значок кнопок, коллекция для дизайна — пятисторонняя форма, -grafiken, -clipart, -cartoons und — круглые серые формы узор калейдоскопа – пятисторонняя форма фото и изображения красивый цветочный узор калейдоскоп – пятисторонние формы фото и изображения Вашингтон, США: Министр обороны США Дональд Рамсфелд выступает во время брифинга в Пентагоне 23 марта 2005 года в Вирджинии.
3D-вектор — пятисторонняя форма сток-графика, -клипарт, -мультфильмы и -символизируйте zitat rahmen leere vorlagen gesetzt. текст в klammern, zitat leere sprechblasen, zitat blasen. textbox isoliert auf pastellfarben hintergrund. — пятисторонняя графика формы, -клипарт, -мультфильмы и -символические абстрактные изображения — пятисторонняя графика формы, -клипарт, -мультфильмы и -символы, элегантные изображения для бизнес-берихта на многоугольнике внутри — пятисторонняя графика формы , -clipart, -cartoons und -symbolegrafik-informationen — пятисторонняя форма, -графика, -clipart, -cartoons und -symboleabstrakte mosaik schneeflocken, собрать значок кнопок, коллекция для дизайна — пятисторонняя форма, -grafiken, -clipart, -cartoons und — круглые серые формы узор калейдоскопа – пятисторонняя форма фото и изображения красивый цветочный узор калейдоскоп – пятисторонние формы фото и изображения Вашингтон, США: Министр обороны США Дональд Рамсфелд выступает во время брифинга в Пентагоне 23 марта 2005 года в Вирджинии. Рамсфелд…пустой медовый сот в улье пасеки пчеловодов puremiel в аркос-де-ла-фронтера, провинция кадис, андалусия, испания мультфильмы и символы Пентагон в Арлингтоне, штат Вирджиния, штаб-квартира Министерства обороны. Обведите пять тематических инфографических дизайнов — пятисторонняя форма, графика, клипарт, мультфильмы и символы. Античная иллюстрация изометрической кристаллической системы (кубическая система, тессеральная система, обычная система) — фото и изображения пятисторонней формы. Эта фотография сделана 29 сентября., 2020 показывает вид с воздуха на лагерь для сирийцев, перемещенных в результате конфликта из провинции Хама, построенный Катаром … кожаный футбольный мяч, рентген — пятисторонняя форма сток-фото и бильдеравстралийский вонючий гриб — пятигранник сток-фото и изображение 1940-х годов 1950-х годов ВИД С ВОЗДУХА ПЕНТАГОН АРЛИНГТОН, Вирджиния, СШАабстрактный многоугольный фон синий — пятисторонняя форма сток-графика, -клипарт, -мультфильмы и -символвекториллюстрация der malbuchseite für kinder mit umrissener Clipart zum ausmalen.
Рамсфелд…пустой медовый сот в улье пасеки пчеловодов puremiel в аркос-де-ла-фронтера, провинция кадис, андалусия, испания мультфильмы и символы Пентагон в Арлингтоне, штат Вирджиния, штаб-квартира Министерства обороны. Обведите пять тематических инфографических дизайнов — пятисторонняя форма, графика, клипарт, мультфильмы и символы. Античная иллюстрация изометрической кристаллической системы (кубическая система, тессеральная система, обычная система) — фото и изображения пятисторонней формы. Эта фотография сделана 29 сентября., 2020 показывает вид с воздуха на лагерь для сирийцев, перемещенных в результате конфликта из провинции Хама, построенный Катаром … кожаный футбольный мяч, рентген — пятисторонняя форма сток-фото и бильдеравстралийский вонючий гриб — пятигранник сток-фото и изображение 1940-х годов 1950-х годов ВИД С ВОЗДУХА ПЕНТАГОН АРЛИНГТОН, Вирджиния, СШАабстрактный многоугольный фон синий — пятисторонняя форма сток-графика, -клипарт, -мультфильмы и -символвекториллюстрация der malbuchseite für kinder mit umrissener Clipart zum ausmalen. buchstabe p für pentagon. — пятисторонняя форма — графика, -клипарт, -мультфильмы и -символы из 37
buchstabe p für pentagon. — пятисторонняя форма — графика, -клипарт, -мультфильмы и -символы из 37152 5 сторонний Стоковые фото, картинки и изображения
5 лет пригласительный билет векторные иллюстрации. двусторонний шаблон современного графического дизайна для приглашения на вечеринку по случаю 5-летия
Значок кости, символ казино. куб изолировал простую иллюстрацию. концепция игры в покер в векторном плоском стиле.
Векторная иллюстрация приглашения на 5-летие. карточка шаблона дизайна
Красочный пятисторонний инфографический шаблон презентации головоломки с пояснительным текстовым полем
Пять шестигранных игральных костей на зеленом фоне
Значок вектора кости. игровой куб казино, черный набор из шести точек на белом фоне. Простая иллюстрация покера
Один изометрический кубик для игры в крэпс, матовый реалистичный материал
Пять брошенных шестигранных кубиков на желтом фоне
Пять шестигранных кубиков на розовом фоне
Два зеленых полупрозрачных пластиковых игровых кубика с белыми точками, запечатленными в воздухе когда их катят по зеркалу с черным фоном.

Два цветных карандаша, двусторонние, красный и синий карандаши на белом фоне
Линейка двусторонняя двусторонняя 50 миллиметров, 5 сантиметров. цена деления 1 мм. точный измерительный инструмент. Калибровочная сетка
Векторная иллюстрация пригласительного билета на 5-летие. двухсторонний шаблон графического дизайна с текстом для приглашения на вечеринку по случаю 5-летия
приглашение на празднование 5-летия векторная иллюстрация
файл шаблона визитной карточки с преимуществами: 1. готовый к печати файл 2. векторный файл 3. текст, размер и цвет можно настроить 4 .каждый отдельный слой 5.файл высокого разрешения
Бургундский стол для казино. песочные часы и покерные фишки на красном фоне
Розовая геометрическая фигура пятиугольника реалистичный трехмерный шаблон вектор пятиугольный пятиугольник
Пара зеленых полупрозрачных пластиковых игральных костей с белыми пятнами, изображающими счастливую цифру семь на гранях куба и на их отражении в черном зеркало, на котором они сидят.

Два цветных карандаша, двусторонние, красный и синий карандаши на белом фоне
Два цветных карандаша, двусторонние, красный и синий карандаши на белом фоне
Кости казино, изолированные на белом фоне. установлен. 3d иллюстрация
Пара зеленых полупрозрачных игровых костей на белом фоне
Бордовый стол казино. песочные часы и фишки для покера на красном фоне
Коллекция дорогих неравных пятиугольных пятиугольных геометрических фигур для маркетинга декора интерьера
Файл шаблона визитной карточки Преимущества: 1. готовый файл для печати 2. векторный файл 3. текст, размер и цвет можно настроить 4 .каждый отдельный слой 5.файл высокого разрешения
Линейка двусторонняя двусторонняя 5000 мм, 500 см, 5 метров. цена деления 1 мм. точный измерительный инструмент. калибровочная сетка
Пригласительный билет на 5-летие, векторная иллюстрация флаера
Белые симметричные фигуры на черном фоне. повторяющиеся пятисторонние многоугольники и другие абстрактные формы.
 бесшовный дизайн поверхности. замкнутые кривые и черточки обои. цифровая бумага. vector art
бесшовный дизайн поверхности. замкнутые кривые и черточки обои. цифровая бумага. vector artТипы токсичных отношений на векторном шаблоне. оскорбительный партнер. адаптивный мобильный сайт с иконками. пошаговое прохождение веб-страницы из 5 экранов. цветовая концепция оскорбительного партнера с линейными иллюстрациями
Кости. игральные кости. значок со стороной куба от одного до шести числа. бросок кубика в крэпс или покер. набор черных значков для азартных игр. шаблон, изолированные на белом фоне. точка на кубе казино. вектор.
Линейка двусторонняя двусторонняя 1500 мм, 150 см, 1,5 метра. цена деления 1 мм. точный измерительный инструмент. калибровочная сетка
Два цветных карандаша, двусторонние, красный и синий карандаши изолированы на белом фоне
Бордовый стол для казино. песочные часы и покерные фишки на красном фоне
Двусторонняя линейка 5 см или 50 мм. величина деления 0,5 мм. прибор для точного измерения длины. калибровочная сетка
Белые симметричные фигуры на черном фоне.
 повторяющиеся пятисторонние многоугольники и различные абстрактные формы. бесшовный дизайн поверхности. замкнутые кривые и черточки обои. цифровая бумага. vector art
повторяющиеся пятисторонние многоугольники и различные абстрактные формы. бесшовный дизайн поверхности. замкнутые кривые и черточки обои. цифровая бумага. vector artБордовый стол для казино. песочные часы и покерные фишки на красном фоне
Золотистый металлик d10 десятигранные игральные кости на пенопластовой поверхности с цифрой 5 на верхней стороне
Медный металлический двадцатигранный кубик d20 на пенопластовой поверхности с 5 на верхней стороне
Бордовый стол для казино. песочные часы и покерные фишки на красном фоне
Набор из шести реалистичных изометрических игральных костей с закругленными краями и углом
Маленькие деревянные игральные кости с написанными на них цифрами, изолированные на белом фоне
Преимущества файла шаблона визитной карточки: 1. Готовый к печати файл 2 . векторный файл 3. текст, размер и цвет можно настроить 4. каждый из них является отдельным слоем 5. файл с высоким разрешением
Векторная иллюстрация приглашения на 5-летие.
 элемент шаблона дизайна с романтическим фоном
элемент шаблона дизайна с романтическим фономБелые пятиугольники на черном фоне. симметричные повторяющиеся пятисторонние многоугольники. бесшовные геометрические фигуры дизайн поверхности картины. замкнутые кривые и черточки обои. цифровая бумага. vector art
Построение звезды с помощью пятиугольников делится на квадраты с пятью сторонами, стороны которых равны по длине. Рисунок винтажной линии или гравировка.
5-летие приглашения векторная иллюстрация
Иконка игральных костей для игры, набор изолированных векторных знаков в квартире
3D иллюстрация пяти шестигранных игральных костей с лицом шесть сверху на черном и золотом фоне. концепция азартных игр и удачи.
Векторная иллюстрация приглашения на 5-летие.
Медные металлические десятигранные кости d10 на пенопластовой поверхности с 5 на верхней стороне
Оскорбительные партнеры вводят векторный инфографический шаблон. элементы дизайна контура презентации токсичных отношений.
 визуализация данных с 5 шагов. информационная диаграмма временной шкалы процесса. макет рабочего процесса с линейными значками
визуализация данных с 5 шагов. информационная диаграмма временной шкалы процесса. макет рабочего процесса с линейными значкамиБургундский стол для казино. песочные часы и покерные фишки на красном фоне
Файл шаблона визитной карточки преимуществ: 1. готовый к печати файл 2. векторный файл 3. текст, размер и цвет можно настроить 4. каждый является отдельным слоем 5. файл с высоким разрешением
линейка двунаправленный двухсторонний 2500 мм, 250 см, 5 метров. цена деления 1 мм. точный измерительный инструмент. калибровочная сетка
Кости казино, изолированные на белом фоне. установлен. 3d-иллюстрация
Медный металлический d12 двенадцатигранный кубик на пенопластовой поверхности с цифрой 5 на верхней стороне
Белые симметричные фигуры на черном фоне. повторяющиеся пятиугольники, ромбы и другие абстрактные фигуры. бесшовный дизайн поверхности. замкнутые кривые и черточки обои. цифровая бумага. векторное искусство
Файл шаблона визитной карточки преимуществ: 1.
 готовый файл для печати 2. векторный файл 3. текст, размер и цвет можно настроить 4. каждый является отдельным слоем 5. файл с высоким разрешением
готовый файл для печати 2. векторный файл 3. текст, размер и цвет можно настроить 4. каждый является отдельным слоем 5. файл с высоким разрешениемДве зеленые, полупрозрачные, пластиковые игры игральные кости с белыми пятнами, запечатленные в воздухе, когда они катятся по зеркалу с черным фоном.
Типы токсичных партнеров на странице мобильного приложения. односторонние отношения, прохождение 5 шагов, графические инструкции с концепциями. векторный шаблон ui, ux, gui с линейными иллюстрациями в ночном режиме
Одна изометрическая игра в кости, матовый фотореалистичный материал, 3D-рендеринг 5 пятисторонний символ. схема геометрии. знак пятиугольной диаграммы. пиктограмма многоугольника. пятиугольная иконка на белой иллюстрации
Приглашение на 5-летие, чтобы отпраздновать векторную иллюстрацию события. элемент шаблона дизайна с номером и текстом для поздравительной открытки на 5-летие, приглашение на вечеринку
Иллюстрация приглашения на 5-летие. шаблон графического дизайна
5-сторонний круглый шаблон презентации с образовательными иконками и местом для текста
Макет инфографического дизайна
Коллекция из трех красочных пластиковых кубиков
Париж, Франция — 5 июня 2017 г.
 : темно-зеленые деревянные металлические знаменитые двухсторонние скамейки расположены в Люксембургском саду среди высоких зеленых деревьев. на заднем плане видна открытая терраса кафе
: темно-зеленые деревянные металлические знаменитые двухсторонние скамейки расположены в Люксембургском саду среди высоких зеленых деревьев. на заднем плане видна открытая терраса кафеНабор из трех цветных пластиковых кубиков
Редактируемый шаблон двусторонней горизонтальной гистограммы, включающий три группы по пять элементов, двухцветная версия
Пара белых кубиков с изображением трех и двух
Приглашение на 5-летие векторная иллюстрация . элемент графического дизайна для поздравительной открытки на 5-летие, приглашение на вечеринку
5-летие приглашения на празднование векторной иллюстрации. элемент графического дизайна с золотым номером для поздравительной открытки на 5-летие, приглашение на вечеринку
Иллюстрация к 5-летнему юбилею. элемент графического дизайна
Пара белых кубиков, изображающих четыре и один
Редактируемый шаблон двусторонней горизонтальной гистограммы, включающий три группы по пять элементов, многоцветная версия
Зеленый стоп-сигнал для движения на школьном перекрестке
5 лет векторная иллюстрация приглашения на годовщину.
 шаблон графического дизайна с золотым элементом для вечеринки по случаю 5-летия или приглашения на ужин.
шаблон графического дизайна с золотым элементом для вечеринки по случаю 5-летия или приглашения на ужин.Приглашение на празднование 5-летия векторной иллюстрации. элемент дизайна с текстом для поздравительной открытки на 5-й день рождения, приглашение на вечеринку
5-летие приглашения на празднование векторной иллюстрации события. элемент дизайна с номером и текстом для поздравительной открытки на 5-й день рождения, приглашения на вечеринку
Коллекция из 9 различных сегментированных инфографических диаграмм с одной и той же темой
Текстовое поле в форме звезды
Пятисторонний шаблон презентации с трехмерными стрелками для брошюр, баннеров, рекламы и бизнес-статистики и инфографика
Шаблоны презентаций инфографики с 2, 3, 4 и 5 элементами
Двусторонний шаблон презентации с пятью полями
Зеленый икосаэдр 20-гранный пронумерованный штамп, Англия, Великобритания, Западная Европа
5-сторонняя бизнес-диаграмма с аватарами бизнесмена и местом для текста и картой мира
Красочный пятисторонний инфографический шаблон презентации головоломки с пояснительным текстовым полем
В форме звезды текстовое поле
Векторная иллюстрация очищенной многослойной банкноты Европейского Союза номиналом 5 евро.

Игра в кости
Платонов додекаэдр 12-гранный кубик, Англия, Великобритания, Западная Европа
Выбор платонических игральных костей, Англия, Великобритания, Западная Европа многоугольник Роялти бесплатно векторное изображение Значок пятиугольника пятисторонний многоугольник Роялти бесплатно векторное изображение
- лицензионные векторы
- Векторы Пентагона
ЛицензияПодробнее
Стандарт Вы можете использовать вектор в личных и коммерческих целях. Расширенный Вы можете использовать вектор на предметах для перепродажи и печати по требованию.Тип лицензии определяет, как вы можете использовать этот образ.
Станд. Расшир. 
Печатный / редакционный Графический дизайн Веб-дизайн Социальные сети Редактировать и изменять Многопользовательский Предметы перепродажи Печать по запросу Способы покупкиСравнить
Плата за изображение € 14,99 Кредиты € 1,00 Подписка € 0,69Оплатить стандартные лицензии можно тремя способами.
 Цены евро евро .
Цены евро евро .Оплата с Цена изображения Плата за изображение € 14,99 Одноразовый платеж Предоплаченные кредиты € 1 Загружайте изображения по запросу (1 кредит = 1 евро). Минимальная покупка 30р. План подписки От 0,69 € Выберите месячный план. Неиспользованные загрузки автоматически переносятся на следующий месяц. Способы покупкиСравнить
Плата за изображение € 39,99 Кредиты € 30,00Существует два способа оплаты расширенных лицензий. Цены евро евро .
Оплата с Стоимость изображения Плата за изображение € 39,99 Оплата разовая, регистрация не требуется. 
Предоплаченные кредиты € 30 Загружайте изображения по запросу (1 кредит = 1 евро). Дополнительные услугиПодробнее
Настроить изображение Доступно только с оплатой за изображение € 85,00Нравится изображение, но нужны лишь некоторые модификации? Пусть наши талантливые художники сделают всю работу за вас!
Мы свяжем вас с дизайнером, который сможет внести изменения и отправить вам изображение в выбранном вами формате.
Примеры
- Изменить текст
- Изменить цвета
- Изменение размера до новых размеров
- Включить логотип или символ
- Добавьте название своей компании или компании
Включенные файлы
Подробности загрузки…
- Идентификатор изображения
- 20716123
- Цветовой режим
- RGB
- Художник
- векторы
Форма пятиугольника – определение, свойства, формулы, примеры
Форма пятиугольника представляет собой плоскую форму или плоскую (двумерную) 5-стороннюю геометрическую форму.
 В геометрии он рассматривается как пятиугольник с пятью прямыми сторонами и пятью внутренними углами, которые в сумме дают 540°. Пятиугольники могут быть простыми или самопересекающимися. Простой пятиугольник (5-угольник) должен иметь пять прямых сторон, которые образуют пять вершин, но не пересекаются друг с другом. Самопересекающийся правильный пятиугольник называется пентаграммой.
В геометрии он рассматривается как пятиугольник с пятью прямыми сторонами и пятью внутренними углами, которые в сумме дают 540°. Пятиугольники могут быть простыми или самопересекающимися. Простой пятиугольник (5-угольник) должен иметь пять прямых сторон, которые образуют пять вершин, но не пересекаются друг с другом. Самопересекающийся правильный пятиугольник называется пентаграммой.1. Что такое Пентагон? 2. Формула Пентагона 3. Свойства Пентагона 4. Примеры формы пятиугольника 5. Район Пентагона 6. Периметр Пентагона 7. Разница между правильными и неправильными пятиугольниками 8. Часто задаваемые вопросы о Пентагоне Что такое Пентагон?
Пятиугольник представляет собой двумерную геометрическую фигуру с пятью сторонами и пятью углами.
 Определение формы пятиугольника происходит от греческого слова «пента» обозначает пять, а «гон» обозначает угол. Пятиугольник – это пятиугольник. Домашняя тарелка, которую можно увидеть на бейсбольном поле, является примером формы пятиугольника.
Определение формы пятиугольника происходит от греческого слова «пента» обозначает пять, а «гон» обозначает угол. Пятиугольник – это пятиугольник. Домашняя тарелка, которую можно увидеть на бейсбольном поле, является примером формы пятиугольника.Формула Пентагона
Формулы пятиугольника помогают нам узнать все о форме пятиугольника. Из общей формулы многоугольников получаем следующую формулу пятиугольников.
- Диагонали пятиугольника: = n × (n − 3) ÷ 2 = 5 × (5 − 3) ÷ 2 = 5
- Сумма внутренних углов пятиугольника: = 180° × (n − 2) = 180° × (5 − 2) = 540°
- Внешний угол пятиугольника: = 540° ÷ n = 540° ÷ 5 = 108°
- Внутренний угол Пентагона: = 360° ÷ n = 360° ÷ 5 = 72°
- Площадь Пентагона = 1/2 × Периметр × Апофема квадратных единиц
- Периметр пятиугольника = (сторона1 + сторона2 +сторона3 + сторона4 + сторона5) единиц
Свойства пятиугольника
Пятиугольник имеет пять прямых сторон, которые не перекрываются.
 Если пять сторон фигуры не соединены или одна сторона фигуры изогнута, то это не пятиугольник. Согласно определению Пентагона, пятиугольник имеет 5 углов.
Если пять сторон фигуры не соединены или одна сторона фигуры изогнута, то это не пятиугольник. Согласно определению Пентагона, пятиугольник имеет 5 углов.Свойства формы пятиугольника Формула формы пятиугольника Стороны = 5 n = 5 Диагонали = 5 n × (n − 3) ÷ 2 Внутренний угол = 72° 360° ÷ N Внешний угол = 108° 540° ÷ N Площадь пятиугольника 1/2 × Периметр × Апофема кв.ед. Периметр пятиугольника s1 + s2 + s3 + s4 + s5 шт. Примеры формы пятиугольника
Есть множество объектов в форме пятиугольника, с которыми мы сталкиваемся в повседневной жизни. Ниже приведены примеры правильных и неправильных пятиугольников. Вы узнаете больше интересных фактов о форме Пентагона, если посмотрите на примеры в форме Пентагона, такие как бамия, симметричная морская звезда и другие подобные объекты.

Можете ли вы классифицировать эти объекты формы пятиугольника и идентифицировать факты формы пятиугольника?
Факты о форме Пентагона
- Пентагон — это штаб-квартира Министерства обороны США в Вашингтоне, округ Колумбия, пример типичной формы Пентагона.
- Президент Рузвельт решил, что во время Второй мировой войны необходимо новое здание для военного министерства.
- Интересной особенностью формы Пентагона было то, что архитектор выбрал форму Пентагона для здания, что сократило расстояние, которое люди должны были пройти от одного офиса до другого.
Район Пентагона
Площадь Пентагона — это площадь, занимаемая в пределах его 5 сторон. Чтобы найти площадь, нам нужно знать, какой у нас пятиугольник и какую информацию мы знаем о нашем пятиугольнике. Обычный пятиугольник можно разделить на 5 треугольников.
Площадь пятиугольника = 5 × площадь треугольника
Площадь пятиугольника = 1/2 × периметр × апофема квадратных единиц в одну из его сторон.
 Его также называют радиусом пятиугольника.
Его также называют радиусом пятиугольника.Площадь пятиугольника Расчет
Рассмотрим треугольник POQ, в котором OA = апофема, а OA перпендикулярен PQ. Предположим, что длина стороны равна 6 дм. Рассмотрим прямоугольный треугольник POA. OP = гипотенуза и AP = 1/2 стороны пятиугольника = 3 дюйма
∠AOP = 36° (∵ 72° ÷ 2)
∠OPA = 54° (∵ 108° ÷ 2)
Тангенс угла
тангенс 36° = противоположный/примыкающий
= противоположный/апофема
= 3/апофема
Апофема = 3/тангенс 36°
= 3/0,72
= 4,16 дюйма
Площадь = 1/2 × 5 × сторона × апофема
= 1/2 × периметр × апофема
= 1/2 × 30 × 4,16
= 15 × 4,16
= 62,4 кв. дюйма
Нестандартное мышление!
- Пентаграмма представляет собой форму звезды, полученную из пяти диагоналей правильного пятиугольника. Это правда?
- Сколько треугольников может быть в таком пятиугольнике с 5 диагоналями? Может действительно 35?
Периметр Пентагона
Периметр правильного или неправильного пятиугольника — это расстояние вокруг его пяти сторон.
 Таким образом, это сумма его сторон.
Таким образом, это сумма его сторон.Периметр пятиугольника = (сторона 1 + сторона 2 + сторона 3 + сторона 4 + сторона 5) единиц
Если все стороны правильного пятиугольника имеют одинаковые размеры, Периметр правильного пятиугольника = 5 × единиц стороны
Если каждая сторона имеет длину 6,3 фута, периметр пятиугольника = 5 × 6,3 = 31,5 фута
Разница между правильными и неправильными пятиугольниками
В зависимости от величины угла и сторон пятиугольника он подразделяется на правильный и неправильный пятиугольник, выпуклый и вогнутый пятиугольник. В таблице показана разница между пятиугольниками.
Правильный пятиугольник Неправильный пятиугольник Все внутренние углы и стороны равны Все внутренние углы и стороны имеют разные размеры Выпуклый пятиугольник Вогнутый пятиугольник Все внутренние углы < 180°, а вершины направлены наружу Один или несколько внутренних углов > 180°, а вершины направлены внутрь Посмотрите на изображение ниже, чтобы визуализировать правильные и неправильные пятиугольники, а также два других типа пятиугольников — вогнутые и выпуклые пятиугольники.

Важные замечания о форме пятиугольника
- Правильный пятиугольник состоит из 10 равнобедренных прямоугольных треугольников.
- Если даны длина стороны и апофема, рассчитайте площадь = 1/2 × периметр × апофема кв. единиц.
- Если известна длина одной стороны, найдите апофему, а затем площадь пятиугольника.
- Апофема = сторона/2 ÷ tan36°.
Похожие статьи о Пентагоне
Ознакомьтесь с интересными статьями о форме пятиугольника. Нажмите, чтобы узнать больше!
- Углы в пятиугольнике
- Район Пентагона
- Калькулятор площади пятиугольника
- Декагон
- Пятиугольная пирамида
Часто задаваемые вопросы о Пентагоне
Что такое пятиугольник в геометрии?
Двумерная фигура с 5 сторонами известна как пятиугольник. Другими словами, мы называем его 5-сторонним многоугольником.
Как называется пятисторонняя фигура?
Пятиугольник называется пятиугольником.
 Если все пять сторон равны, то мы называем его правильным пятиугольником, а если любые две стороны различны по размеру, мы называем его неправильным пятиугольником. С другой стороны, шестиугольник — это шестиугольник, а восьмиугольник — восьмиугольник.
Если все пять сторон равны, то мы называем его правильным пятиугольником, а если любые две стороны различны по размеру, мы называем его неправильным пятиугольником. С другой стороны, шестиугольник — это шестиугольник, а восьмиугольник — восьмиугольник.Является ли пятиугольник параллелограммом?
Нет, пятиугольник — это не параллелограмм, это пятиугольник. Параллелограмм имеет только четыре стороны.
В чем сходство четырехугольника и пятиугольника?
Четырехугольник и пятиугольник являются замкнутыми многоугольниками, сумма внешних углов которых равна 360°.
Есть ли у пятиугольника симметрия?
Правильный пятиугольник имеет 5 осей симметрии. У неправильного пятиугольника нет линии симметрии.
Какое наибольшее количество параллельных сторон в пятиугольнике?
В правильном пятиугольнике нет параллельных линий, а в неправильном пятиугольнике может быть 2 (1 пара) или 4 (2 пары) параллельных линий.
Сколько углов в пятиугольнике?
Пятиугольник имеет пять углов.
 В случае правильного пятиугольника каждый из этих пяти внутренних углов равен 72° каждый.
В случае правильного пятиугольника каждый из этих пяти внутренних углов равен 72° каждый.Какова сумма внутренних углов пятиугольника?
Сумма всех пяти внутренних углов пятиугольника равна 540°.
Сколько линий симметрии имеет фигура пятиугольника?
Правильный пятиугольник имеет 5 осей симметрии.
Какой внешний угол у пятиугольника?
Внешний угол пятиугольника равен 108°.
Как нарисовать идеальную 5-конечную звезду в Photoshop
Узнайте, как легко нарисовать идеальную 5-конечную звезду или 5-конечную звезду в Photoshop! И как сохранить звезду как пользовательскую форму, чтобы вам больше никогда не пришлось ее рисовать. Для Photoshop 2021 или более поздней версии.
Автор сценария Стив Паттерсон.

В этом уроке я покажу вам, как нарисовать идеальную пятиконечную звезду в Photoshop. Под «идеальной» я подразумеваю звезду, у которой стороны звездных сегментов идеально совпадают друг с другом. Теперь Photoshop включает в себя несколько встроенных форм звезд, но ни одна из них не выглядит правильно. Итак, я покажу вам, как легко нарисовать свою собственную, и как сохранить звезду как пользовательскую форму, чтобы вам никогда не пришлось рисовать ее снова.
Вот как будет выглядеть звезда, когда мы закончим. Конечно, вы можете выбрать любой понравившийся вам цвет:
Идеальная пятиконечная звезда, нарисованная в Photoshop.
Начнем!
Какая версия Photoshop мне нужна?
Прежде чем мы начнем, я должен отметить, что Adobe внесла изменения в инструменты формы в Photoshop 2021, которые я использую. Поэтому для продолжения вам понадобится Photoshop 2021 или новее. Загрузите последнюю версию Photoshop здесь.
Шаг 1. Создайте новый документ Photoshop
Начните с создания нового документа, который мы будем использовать для рисования звезды.
 Если вы находитесь на главном экране Photoshop, нажмите кнопку Создать новый :
Если вы находитесь на главном экране Photoshop, нажмите кнопку Создать новый :Щелкните
Создать новый
на главном экране.Или, если вы находитесь в основном интерфейсе Photoshop, перейдите в меню File в строке меню и выберите New :
.Выберите «Файл» > «Создать» в строке меню.
В диалоговом окне «Новый документ» выберите Размер Photoshop по умолчанию 9.0781 :
Выбор размера документа по умолчанию.
Затем нажмите Создать :
Нажатие кнопки «Создать».
И появляется новый документ:
Новый документ Photoshop.
Шаг 2. Выберите инструмент «Многоугольник»
Чтобы нарисовать звезду, мы воспользуемся инструментом Photoshop Polygon Tool. На панели инструментов щелкните и удерживайте инструмент Rectangle Tool (или любой другой инструмент формы, который вы использовали последним), пока не появится всплывающее меню:
Щелкните и удерживайте инструмент «Прямоугольник».

И выберите Polygon Tool из списка:
Выбор инструмента «Многоугольник».
Шаг 3. Сброс параметров инструмента
Затем на панели параметров щелкните правой кнопкой мыши (Win) / , удерживая клавишу Control, щелкните (Mac) на значке инструмента:
Щелкните правой кнопкой мыши (Win)/щелчок, удерживая клавишу Control (Mac), на значке инструмента.
И выберите в меню Reset Tool :
Сброс параметров инструмента «Многоугольник».
Это должно установить Режим инструмента от до Форма (не траектория или пиксели):
Режим инструмента должен быть установлен на Shape.
И он должен установить Number of Sides для многоугольника на 5 (поскольку нам нужна 5-конечная звезда) и Corner Radius на 0 (таким образом, мы рисуем звезду с острыми углами):
Количество сторон = 5, Угловой радиус = 0.

Шаг 4. Выберите цвет заливки
Вы можете выбрать цвет фигуры, нажав кнопку Образец цвета заливки :
Щелкните образец цвета заливки.
Затем щелкните значок Color Picker :
Щелкните значок палитры цветов.
И выбор цвета из палитры цветов. Любой цвет будет работать. Я выберу темно-фиолетовый, установив для Hue (H) значение 280 , для параметра Saturation (S) значение 75 и для параметра Brightness (B) значение 40. Нажмите OK, чтобы закрыть окно. Выбор цвета, когда вы закончите:
Выбор цвета фигуры.
Шаг 5: Отключите ход
По умолчанию Photoshop добавляет черную обводку толщиной 1 пиксель вокруг фигур, чего я не хочу. Так что все еще на панели параметров я щелкну образец цвета Stroke :
.Щелкните образец цвета обводки.
И я выберу вариант Нет цвета .
 Затем я нажму Enter (Win) / Return (Mac), чтобы закрыть диалоговое окно:
Затем я нажму Enter (Win) / Return (Mac), чтобы закрыть диалоговое окно:Выбор «Без цвета» для обводки.
Шаг 6. Нарисуйте форму многоугольника
Далее мы нарисуем начальную форму многоугольника. Щелкните в левом верхнем углу холста, чтобы задать начальную точку для фигуры, удерживайте нажатой кнопку мыши и начните перетаскивать в правый нижний угол:
Нажмите и перетащите, чтобы начать рисовать фигуру.
Как только вы начали перетаскивание, нажмите и удерживайте клавишу Shift на клавиатуре, чтобы ограничить фигуру, чтобы все пять сторон были одинаковой длины, и продолжайте перетаскивание:
Удерживая клавишу Shift при перетаскивании, можно сделать все пять сторон одинаковой длины.
Вы можете перемещать и изменять положение фигуры по мере ее рисования, удерживая нажатой клавишу Shift, удерживая клавишу пробела на клавиатуре (таким образом, Shift+пробел) и перетаскивая фигуру на место.
 Я подниму его немного выше:
Я подниму его немного выше:Добавьте пробел, чтобы перемещать фигуру по мере ее рисования.
Затем отпустите пробел, но снова удерживайте нажатой клавишу Shift и продолжайте перетаскивать остальную часть фигуры:
Рисование оставшейся части многоугольника.
Когда вы закончите, отпустите кнопку мыши, затем отпустите клавишу Shift, и Photoshop заполнит фигуру выбранным вами цветом:
Отпустите кнопку мыши (затем клавишу Shift), чтобы завершить фигуру.
Шаг 7. Уменьшите звездность
На данный момент у нас есть пятисторонний многоугольник со всеми пятью сторонами одинаковой длины. Но как превратить его в звезду?
Ответ находится на панели свойств . Здесь вы найдете вариант Star Ratio со значком, который выглядит как звезда внутри большего многоугольника. По умолчанию установлено значение 100 процентов :
.Параметр «Звездность» на панели «Свойства».
Соотношение звезд относится к размеру звезды внутри многоугольника.
 Таким образом, при 100 процентах звезда занимает 100 процентов максимальной площади внутри фигуры, поэтому она не выглядит как звезда. Но по мере того, как мы уменьшаем значение (нажав на значок Star Ratio, удерживая кнопку мыши нажатой и перетаскивая ее влево):
Таким образом, при 100 процентах звезда занимает 100 процентов максимальной площади внутри фигуры, поэтому она не выглядит как звезда. Но по мере того, как мы уменьшаем значение (нажав на значок Star Ratio, удерживая кнопку мыши нажатой и перетаскивая ее влево):Понижение значения звездности.
Обратите внимание, что края многоугольника начинают изгибаться внутрь, и начинает появляться звезда (вам нужно отпустить кнопку мыши, чтобы форма обновилась):
Понижение коэффициента создает форму звезды.
Чтобы преобразовать многоугольник в идеальную звезду, где стороны сегментов совпадают друг с другом, уменьшите соотношение звезд до 47 процентов :
Установка соотношения звезд на 47 процентов.
И теперь сегменты звезды идеально подходят:
Идеальная звезда.
Шаг 8. Сохраните звезду как пользовательскую форму
Вот как легко нарисовать идеальную 5-конечную звезду в Photoshop. Но на этом этапе все становится еще проще, потому что теперь, когда мы нарисовали звезду один раз, мы можем сохранить ее как пользовательскую форму и больше никогда не рисовать ее.

Создание новой группы фигур
Но прежде чем мы это сделаем, давайте создадим новую группу фигур для хранения наших пользовательских фигур. Откройте панель Shapes , перейдя на Окно меню и выбор Shapes :
Перейдите в меню «Окно» > «Фигуры».
Затем на панели Фигуры щелкните значок Новая группа внизу:
Создание новой группы фигур.
Дайте группе имя, например
Мои фигуры
, и нажмите OK:Присвоение имени новой группе.
Новая группа появляется ниже остальных. Если вы уже создали группу в прошлом, убедитесь, что она выбрана, так как мы хотим, чтобы к ней была добавлена форма звезды:
Новая группа фигур.
Создание новой пользовательской формы
Затем перейдите в меню Edit в строке меню и выберите Define Custom Shape :
.Перейдите в меню «Правка» > «Определить пользовательскую форму».

Дайте фигуре имя. Я назову его
Perfect 5 Point Star
. Затем нажмите OK:Присвоение имени новой пользовательской форме.
Вернувшись на панель «Фигуры», звезда появляется в виде миниатюры внутри группы:
Форма звезды добавлена как пользовательская форма.
Как использовать пользовательскую форму звезды
Поскольку мы сохранили звезду как пользовательскую фигуру, я удалю исходную звезду, перейдя на панель «Слои» и перетащив слой с фигурой в корзину:
Удаление исходной формы звезды на панели «Слои».
В следующий раз, когда вам понадобится нарисовать идеальную 5-конечную звезду, просто откройте панель «Фигуры» («Окно» > «Фигуры») и перетащите звезду с панели в документ:
Перетаскивание формы звезды.
Отпустите кнопку мыши, и сразу же появится звезда. Перетащите маркеры , чтобы изменить размер звезды по мере необходимости, а затем нажмите . Введите (Win) / Return (Mac), чтобы принять его:
Звезда рисуется, когда вы отпускаете кнопку мыши.

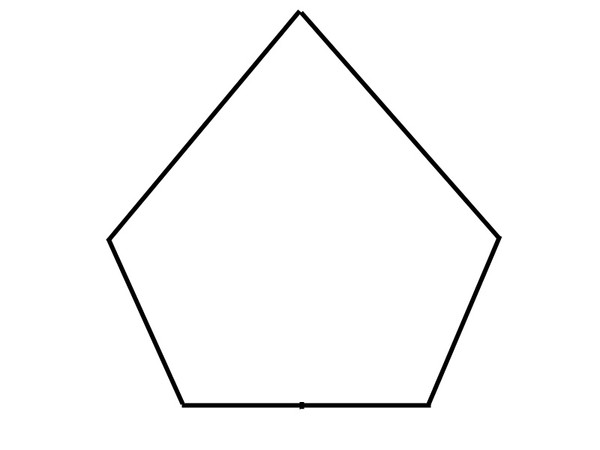 <4>=3Phi +2=<frac <3<sqrt <5>>+7><2>>approx 6<,>8541>где Φ <displaystyle Phi >— отношение золотого сечения.
<4>=3Phi +2=<frac <3<sqrt <5>>+7><2>>approx 6<,>8541>где Φ <displaystyle Phi >— отношение золотого сечения.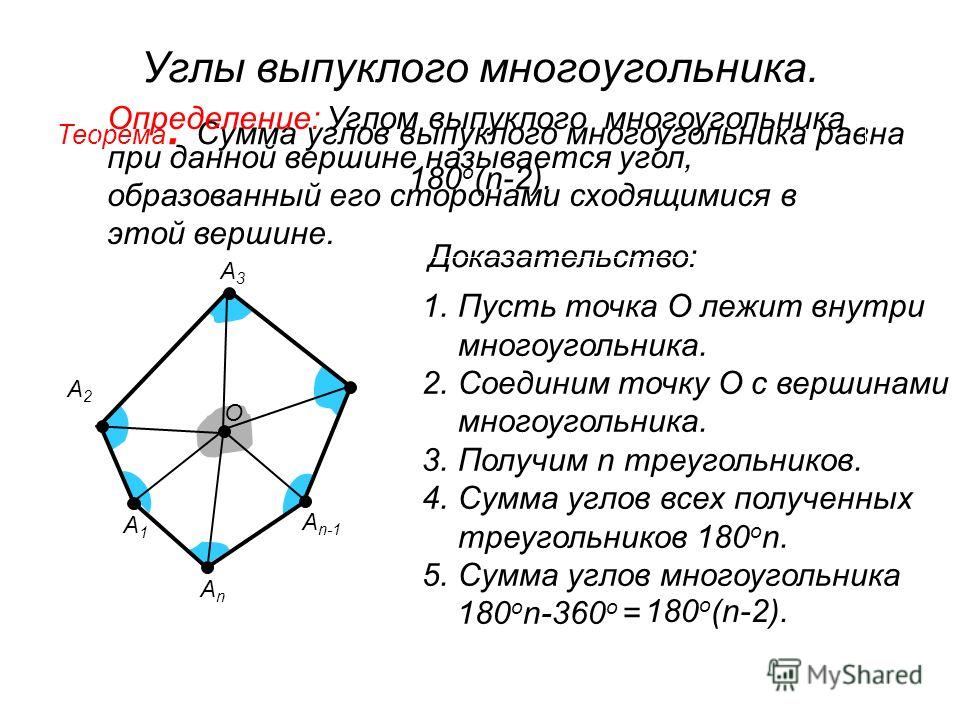
 [1] Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как эта мушмула германская.
[1] Пентасимметрию можно увидеть во многих цветах и некоторых фруктах, например в таких как эта мушмула германская.



 От этого зависит ваш авторитет художника, а значит и заказы.
От этого зависит ваш авторитет художника, а значит и заказы.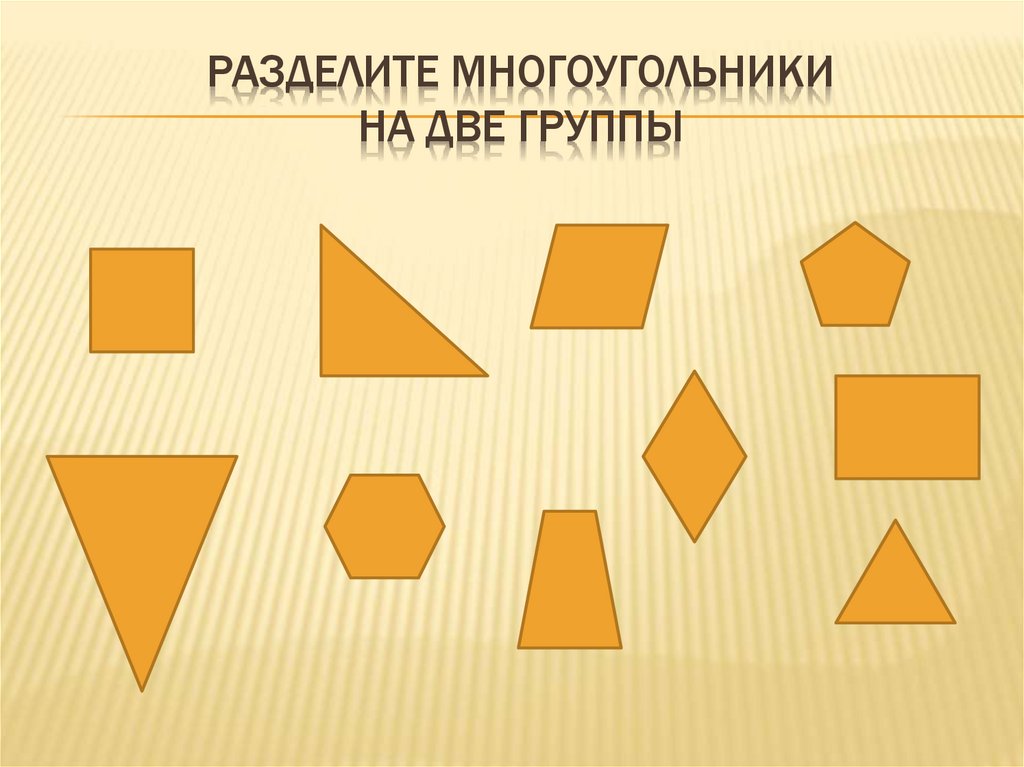

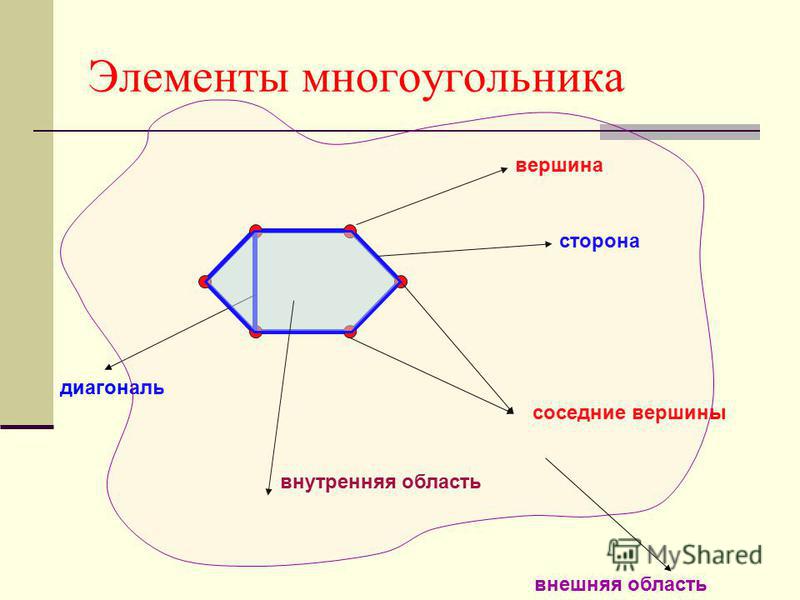
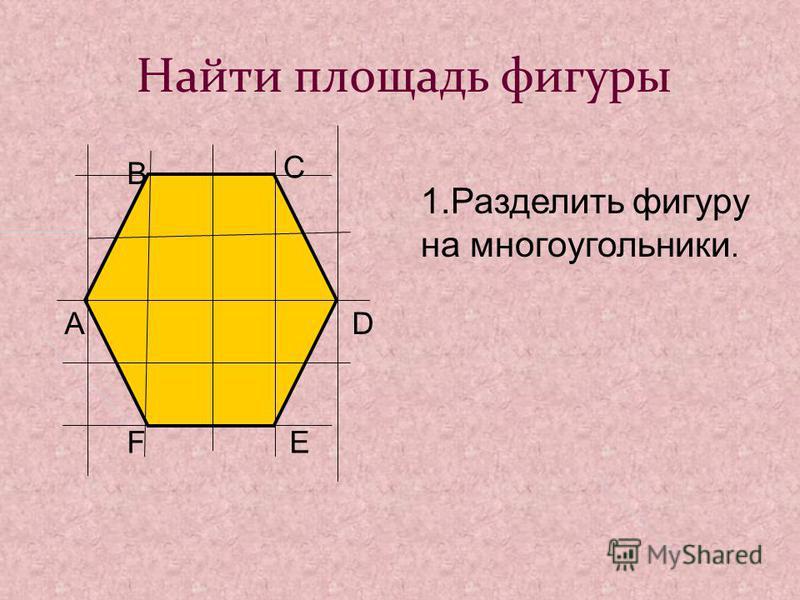 Правильными многоугольниками могут быть только выпуклые многоугольники.
Правильными многоугольниками могут быть только выпуклые многоугольники.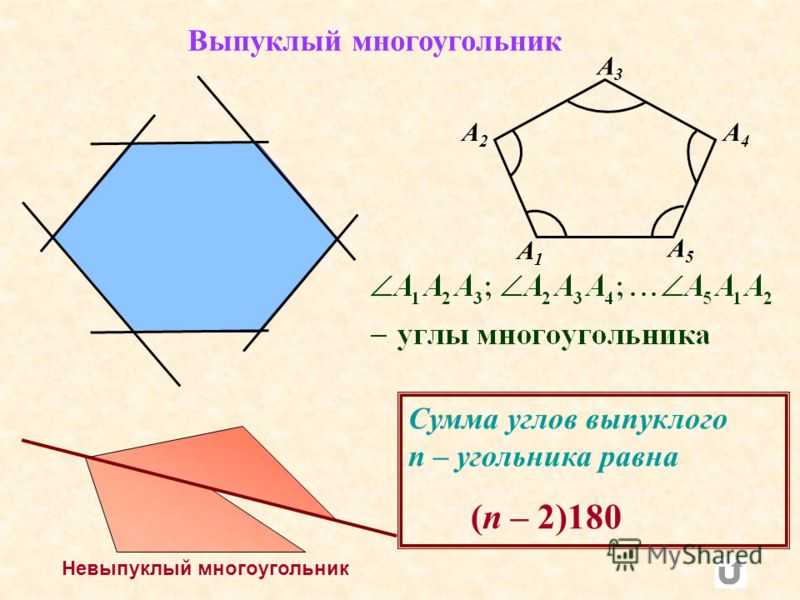
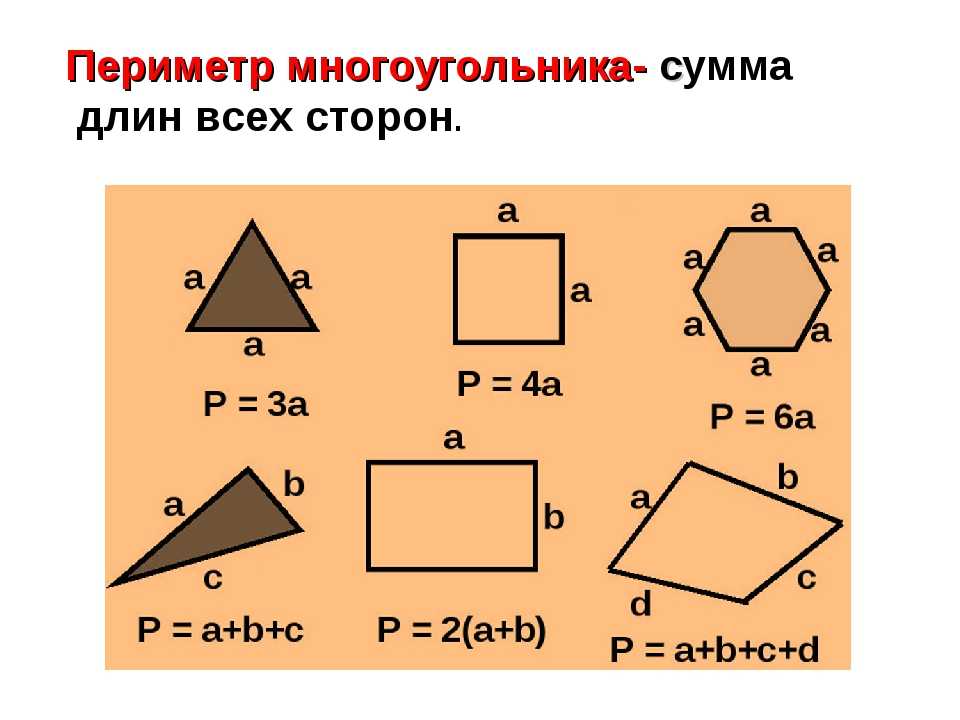
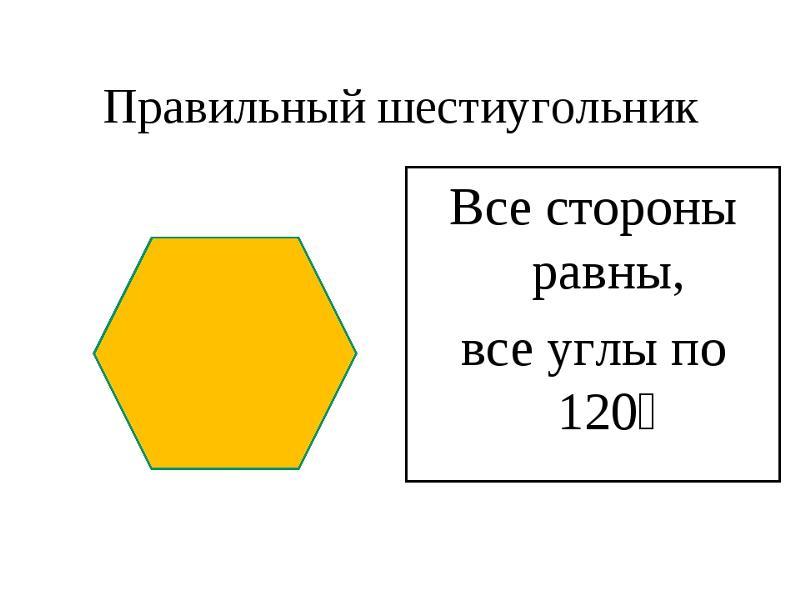 У ученика здесь есть та самая, упомянутая выше, возможность “возиться” с объектами.
У ученика здесь есть та самая, упомянутая выше, возможность “возиться” с объектами. desmos.com/calculator/ddakrfrdtl
desmos.com/calculator/ddakrfrdtl
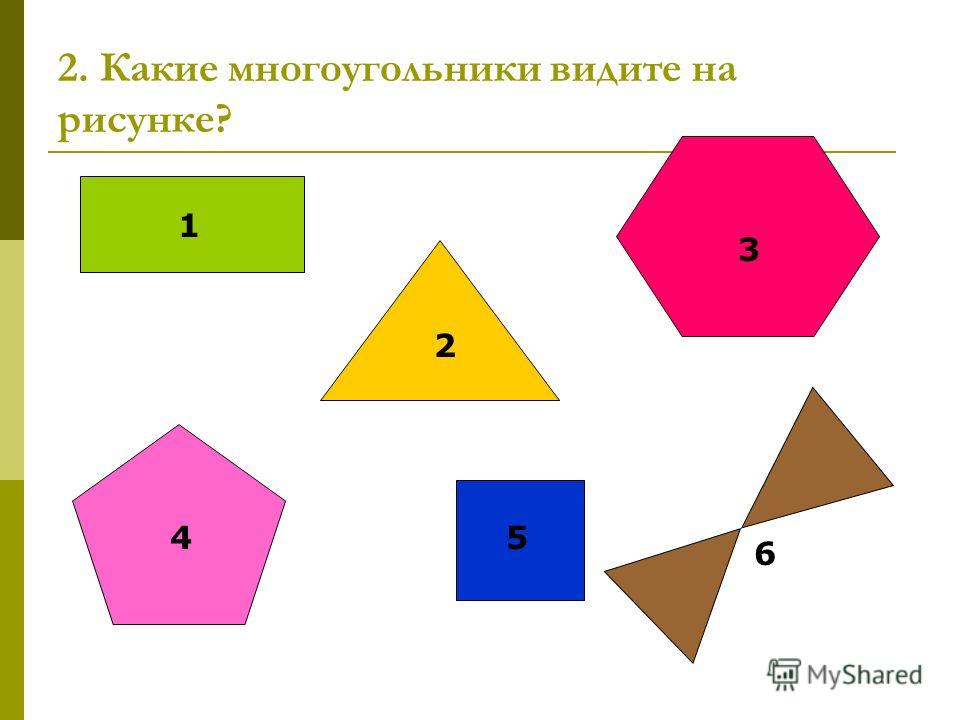
 Между концами этих радиусов внутри двух кругов проведем линию с одной конечной точкой в месте касания к внутреннему кругу и другой точкой в месте касания к внешнему кругу. Радиус — отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка R. Радиус составляет половину диаметра 2R.
Между концами этих радиусов внутри двух кругов проведем линию с одной конечной точкой в месте касания к внутреннему кругу и другой точкой в месте касания к внешнему кругу. Радиус — отрезок, соединяющий центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка R. Радиус составляет половину диаметра 2R.
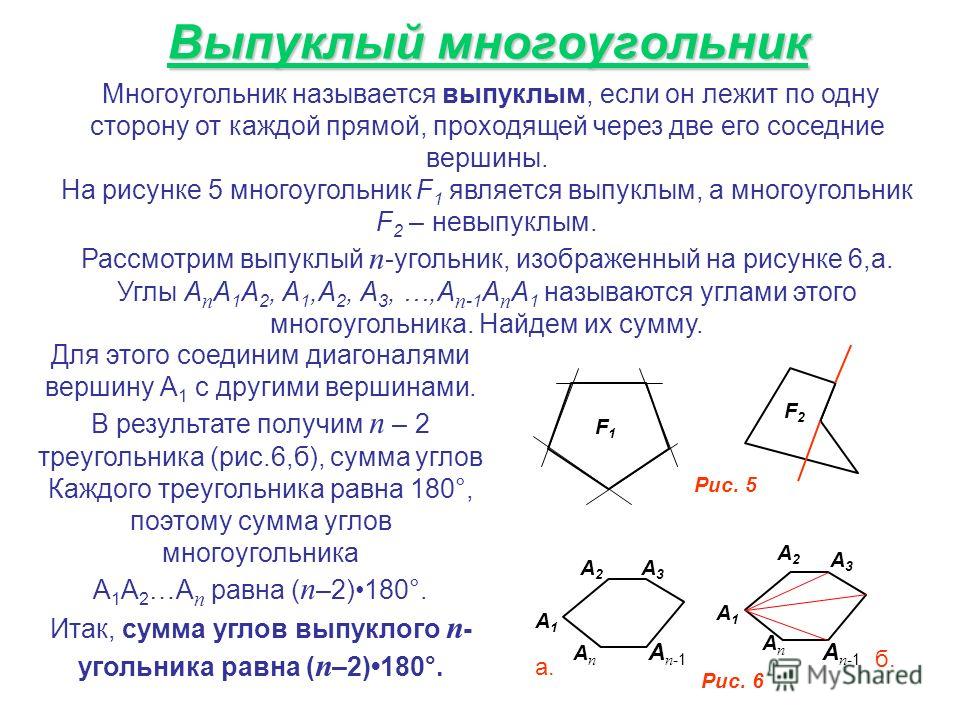
 google.com/store/search?q=Frink+programming+language&c=apps и http://futureboy.us/frinkdocs/frinkframe.html . Один из способов реализовать использование языка-программирования Фринк, это загрузить его в настольный компьютер, который будет использоваться. После того как приложение заработает в среде рабочего стола, его можно будет отправить в сотовый телефон по проводному или беспроводному соединению. После загрузки в телефон, «приложение» может быть использовано там, как калькулятор. Онлайн калькуляторов расчета углов, для многоугольников,в интернете тоже предостаточно:
google.com/store/search?q=Frink+programming+language&c=apps и http://futureboy.us/frinkdocs/frinkframe.html . Один из способов реализовать использование языка-программирования Фринк, это загрузить его в настольный компьютер, который будет использоваться. После того как приложение заработает в среде рабочего стола, его можно будет отправить в сотовый телефон по проводному или беспроводному соединению. После загрузки в телефон, «приложение» может быть использовано там, как калькулятор. Онлайн калькуляторов расчета углов, для многоугольников,в интернете тоже предостаточно: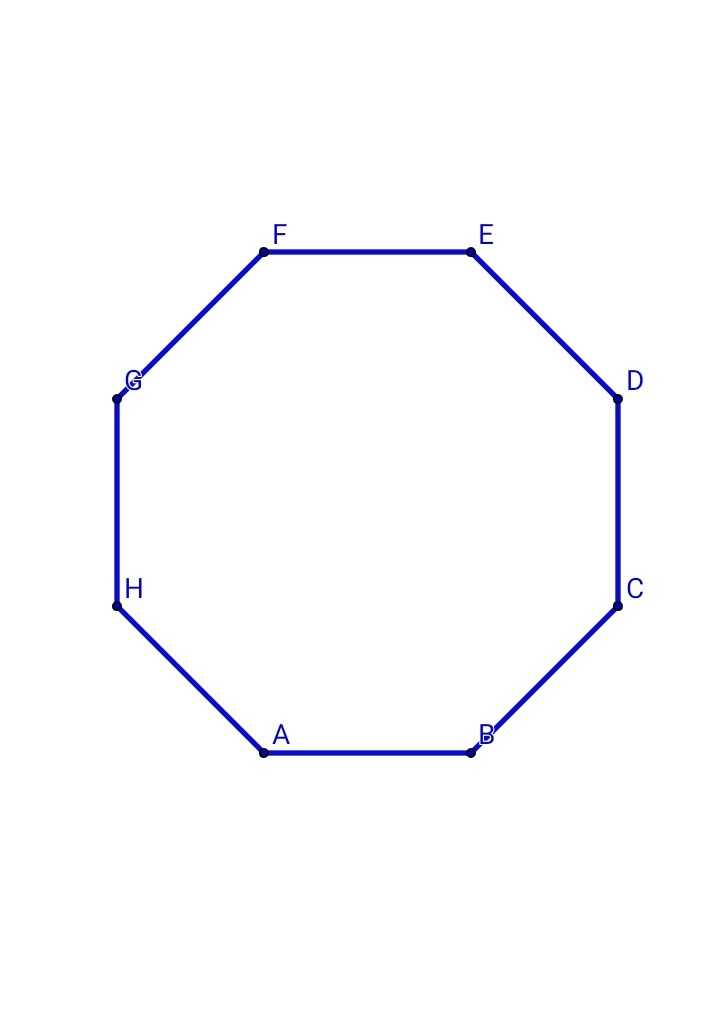
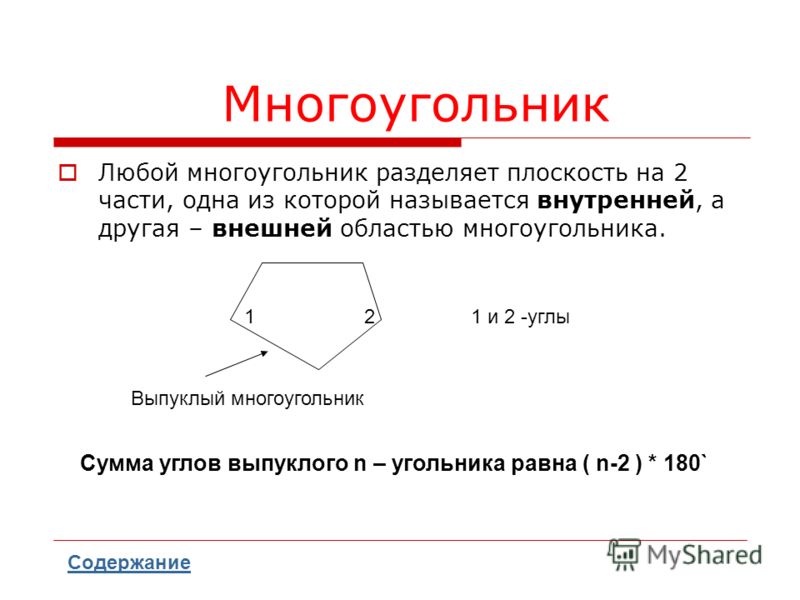 С Авой Фрэнк познакомился на съемках фильма «Джентльмены предпочитают блондинок». Молодая актриса не просто попала в список Синатры, она оказалась там единственной. Фрэнк настолько сильно увлекся Гарднер, что буквально вымаливал у своей супруги развод. После долгих уговоров Нэнси согласилась: Синатра и Гарднер обвенчались. Но…
С Авой Фрэнк познакомился на съемках фильма «Джентльмены предпочитают блондинок». Молодая актриса не просто попала в список Синатры, она оказалась там единственной. Фрэнк настолько сильно увлекся Гарднер, что буквально вымаливал у своей супруги развод. После долгих уговоров Нэнси согласилась: Синатра и Гарднер обвенчались. Но… Все это, безусловно, тешило самолюбие молодого артиста, он был невероятно заносчив, постоянно грубил, что жутко расстраивало Аву. В 1953 году их отношениям пришел конец. И для Синатры это обернулось настоящей трагедией.
Все это, безусловно, тешило самолюбие молодого артиста, он был невероятно заносчив, постоянно грубил, что жутко расстраивало Аву. В 1953 году их отношениям пришел конец. И для Синатры это обернулось настоящей трагедией.
 под номером 1).
под номером 1).
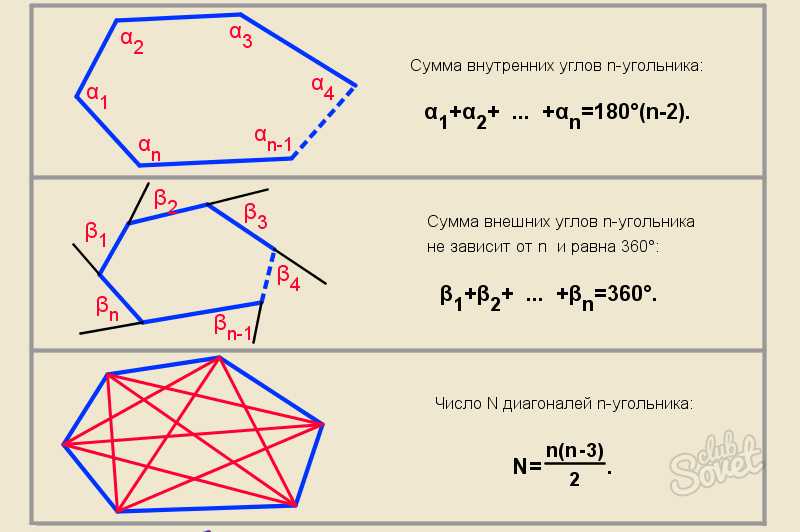 Что означает это странное слово? И почему это боке в фотографии так всем нравится? Давайте разберемся вместе!
Что означает это странное слово? И почему это боке в фотографии так всем нравится? Давайте разберемся вместе! Это зависит от конструктивных особенностей конкретного объектива, которые влияют на форму боке. Посмотрим, какие виды боке встречаются и отчего это зависит.
Это зависит от конструктивных особенностей конкретного объектива, которые влияют на форму боке. Посмотрим, какие виды боке встречаются и отчего это зависит. Традиционно считается, что идеальное боке с точки зрения художественности – это круглое пятно, которое дает объектив идеальной конструкции с максимально открытой диафрагмой. Однако интересного эффекта можно добиться и с объективами, которые рисуют боке в фотографии в виде многоугольника.
Традиционно считается, что идеальное боке с точки зрения художественности – это круглое пятно, которое дает объектив идеальной конструкции с максимально открытой диафрагмой. Однако интересного эффекта можно добиться и с объективами, которые рисуют боке в фотографии в виде многоугольника. Это мягкое боке, которое дает плавное и мягкое размытие. Множество размытых таким образом пятен накладываются друг на друга неяркими (размытыми) краями, и получается плавное размытие фона.
Это мягкое боке, которое дает плавное и мягкое размытие. Множество размытых таким образом пятен накладываются друг на друга неяркими (размытыми) краями, и получается плавное размытие фона. Теперь максимально открывайте диафрагму, фокусируйтесь на главном объекте и нажимайте кнопку спуска. Вуаля! Фотография с красивым боке у вас в портфолио!
Теперь максимально открывайте диафрагму, фокусируйтесь на главном объекте и нажимайте кнопку спуска. Вуаля! Фотография с красивым боке у вас в портфолио!
 Посмотрите:
Посмотрите:

 Раньше для этого требовалось много вычислительной мощности и дорогих суперкомпьютеров.
Раньше для этого требовалось много вычислительной мощности и дорогих суперкомпьютеров.
 Однако, если вам не нравится какой-либо из них, вы можете просто создать свою собственную цветовую схему с помощью 24-битной палитры цветов, предлагаемой в программе.
Однако, если вам не нравится какой-либо из них, вы можете просто создать свою собственную цветовую схему с помощью 24-битной палитры цветов, предлагаемой в программе.
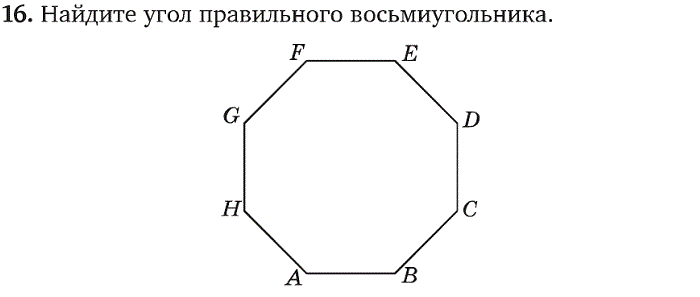 В этом дизайне ни одна из точек не находится внутри описанной окружности других треугольников. Это означает, что эта конструкция максимально избегает острых углов и в результате дает очень широкие и большие формы.
В этом дизайне ни одна из точек не находится внутри описанной окружности других треугольников. Это означает, что эта конструкция максимально избегает острых углов и в результате дает очень широкие и большие формы.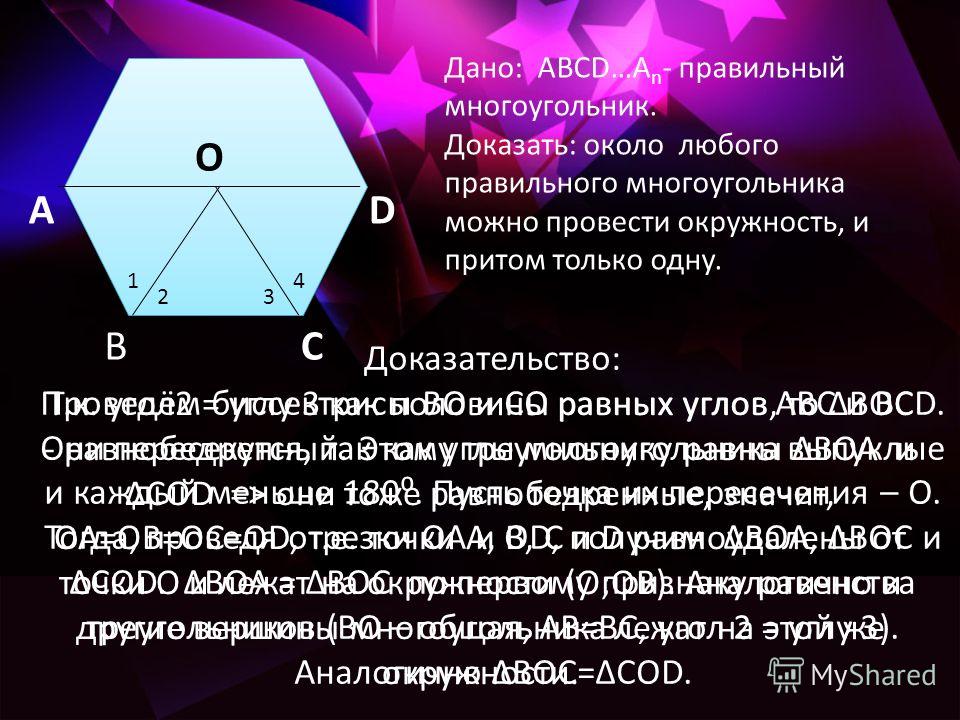 Но это дает большой контроль.
Но это дает большой контроль.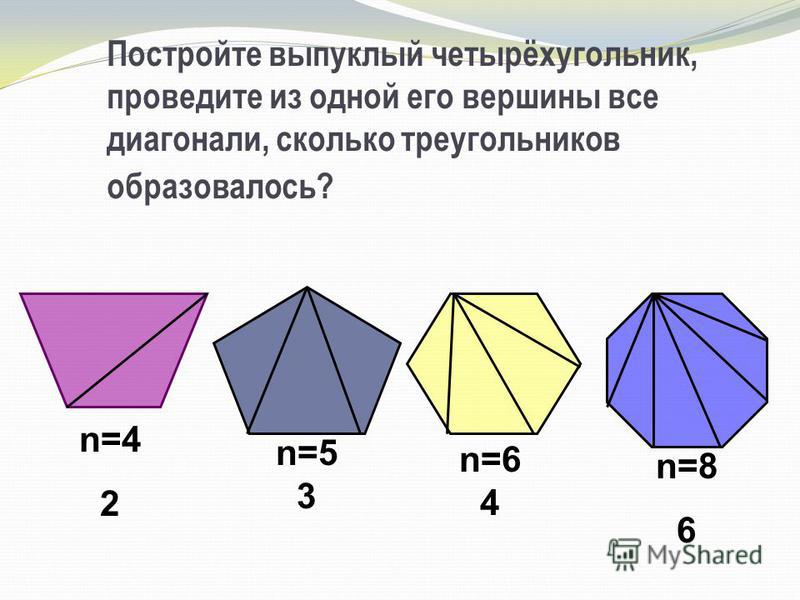
 -используем еще и мощный .
-используем еще и мощный . Но он может быть полезен дизайнерам, которые в основном работают в дороге и на своих телефонах, чтобы создавать изображения, идеально подходящие для их мобильных проектов.
Но он может быть полезен дизайнерам, которые в основном работают в дороге и на своих телефонах, чтобы создавать изображения, идеально подходящие для их мобильных проектов. I ♥ Δ
I ♥ Δ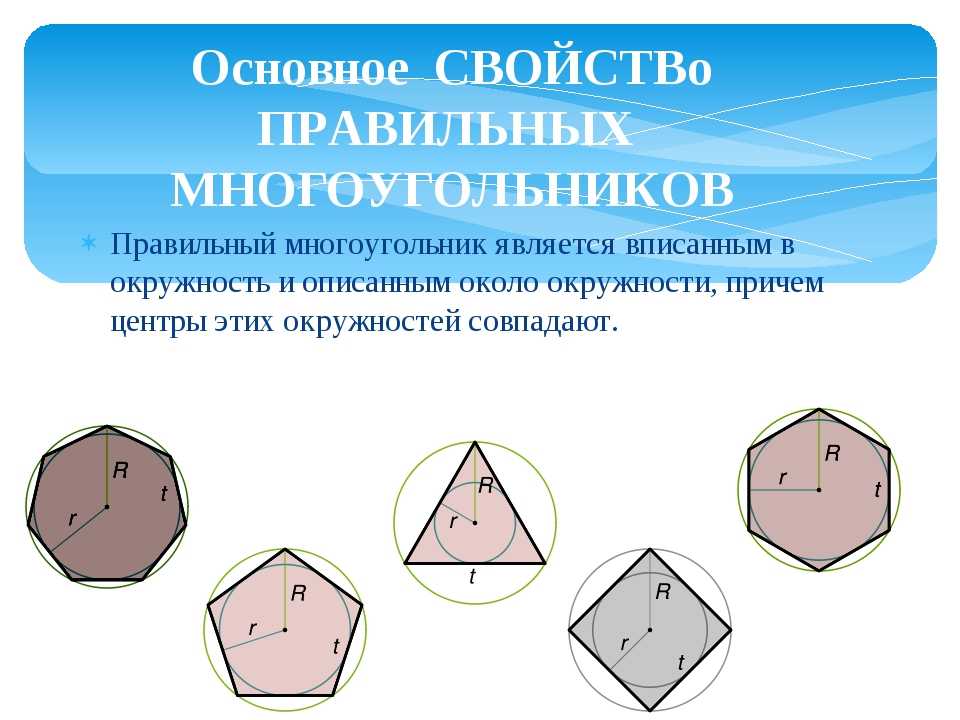 поли изображения на основе изображения.Вы просто перетаскиваете изображение в него . Как только он появится, вы сможете контролировать количество точек, ширину обводки, размытие и точность.
поли изображения на основе изображения.Вы просто перетаскиваете изображение в него . Как только он появится, вы сможете контролировать количество точек, ширину обводки, размытие и точность.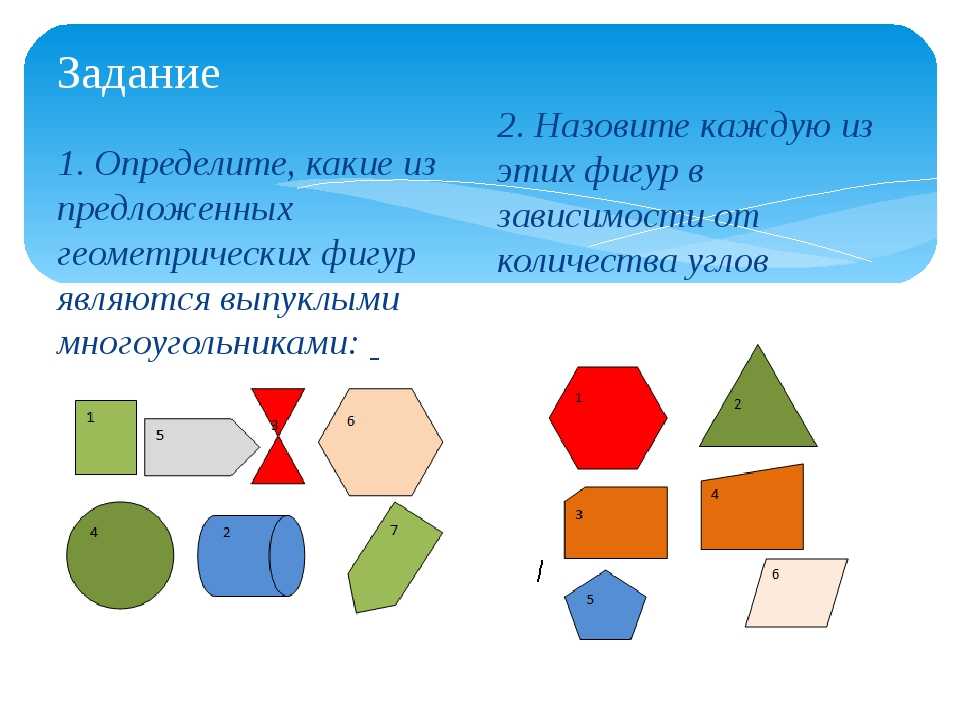


 uk.com
uk.com Это необходимо сделать за 24 часа до окончания бесплатного пробного периода или периода подписки, чтобы избежать списания средств.
Это необходимо сделать за 24 часа до окончания бесплатного пробного периода или периода подписки, чтобы избежать списания средств.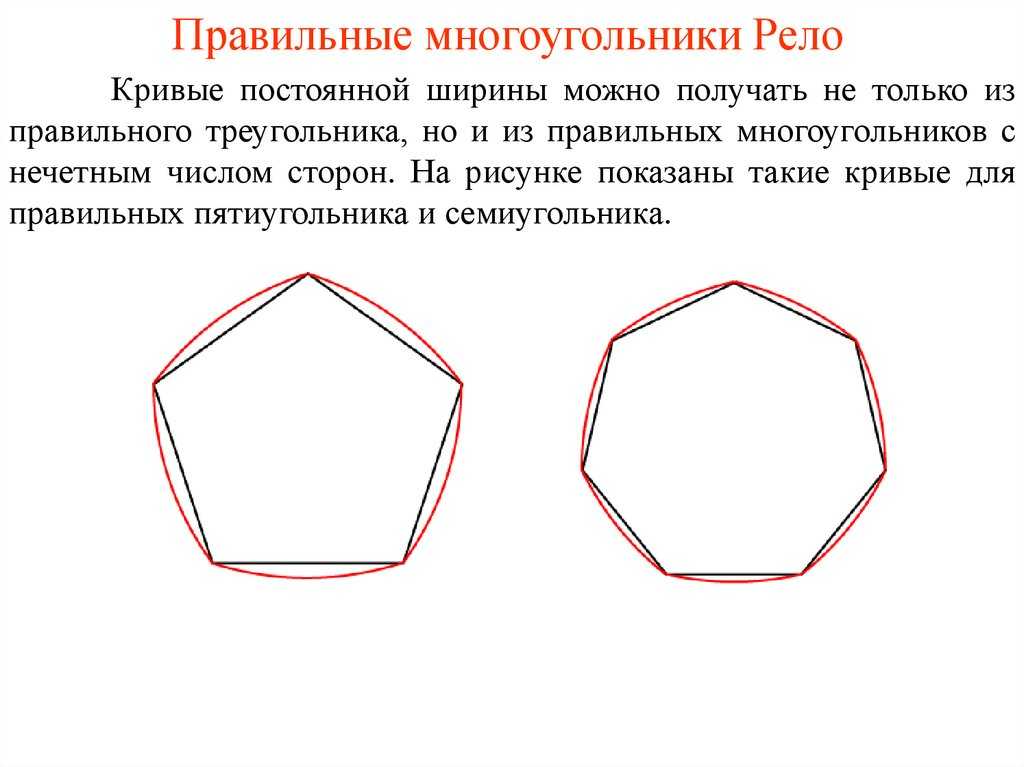
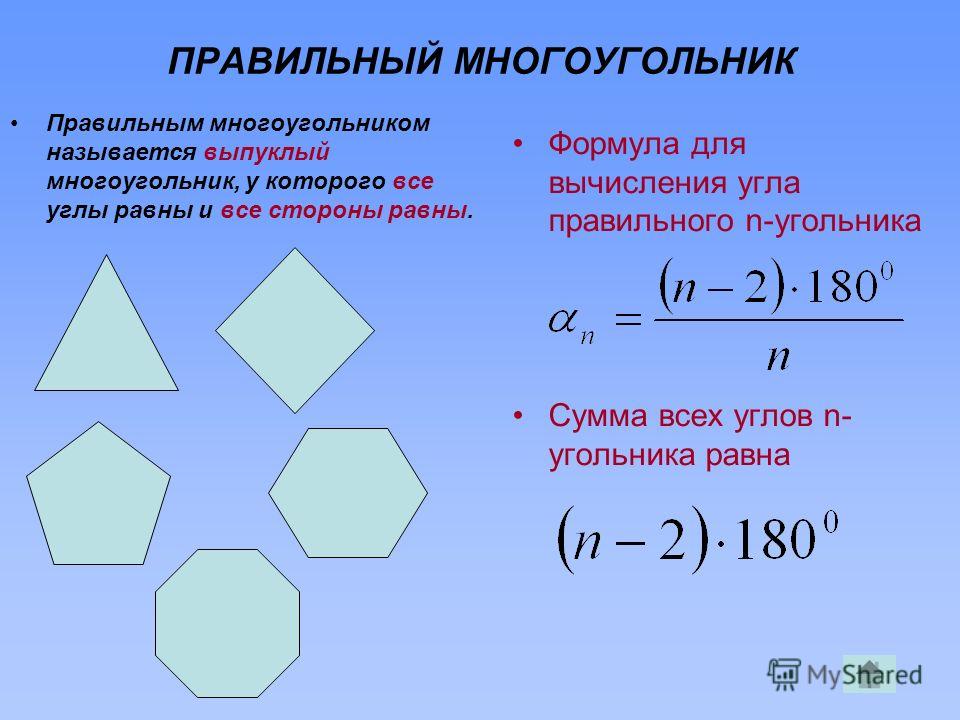 При желании вы можете контролировать процесс, а также легко «заблокировать» свои любимые атрибуты.Редактировать вершины фигур также просто: нажмите, чтобы создать одну, или нажмите на существующую, чтобы удалить ее.
При желании вы можете контролировать процесс, а также легко «заблокировать» свои любимые атрибуты.Редактировать вершины фигур также просто: нажмите, чтобы создать одну, или нажмите на существующую, чтобы удалить ее. Чтобы добраться до него, щелкните инструмент «Лассо», затем удерживайте кнопку мыши нажатой, пока не появится всплывающее меню с дополнительными доступными инструментами.Выберите инструмент Polygonal Lasso Tool из списка:
Чтобы добраться до него, щелкните инструмент «Лассо», затем удерживайте кнопку мыши нажатой, пока не появится всплывающее меню с дополнительными доступными инструментами.Выберите инструмент Polygonal Lasso Tool из списка:
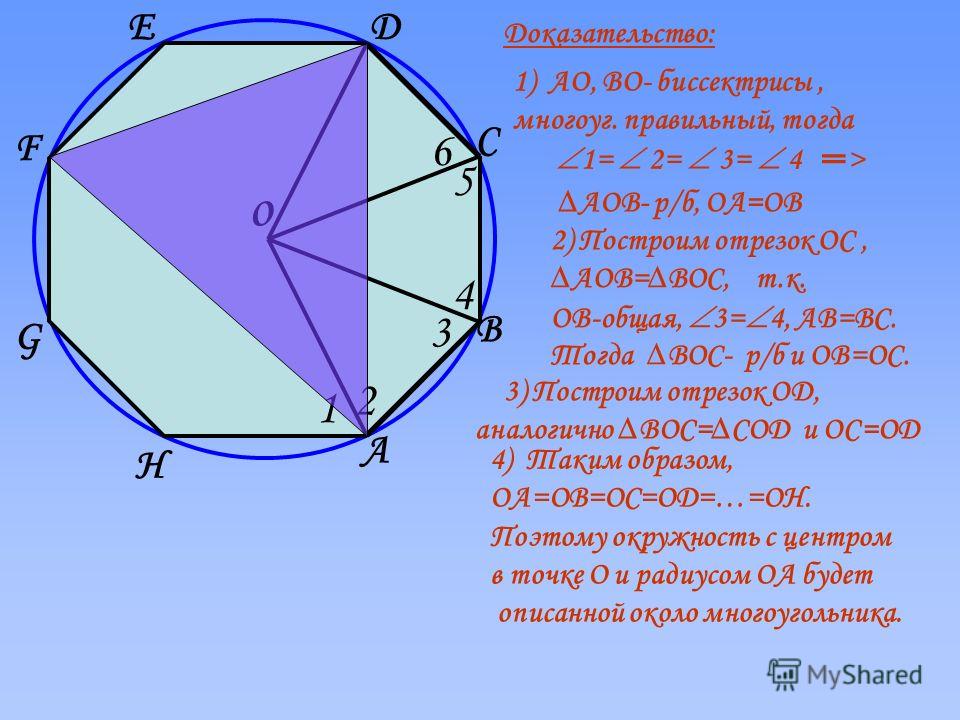 В отличие от стандартного инструмента «Лассо», а также многих других инструментов выделения Photoshop, нет необходимости удерживать кнопку мыши нажатой при перемещении от точки к точке. Просто щелкните, чтобы добавить точку, отпустите кнопку мыши, перейдите к следующему месту, где линия должна изменить направление, затем щелкните, чтобы добавить новую точку:
В отличие от стандартного инструмента «Лассо», а также многих других инструментов выделения Photoshop, нет необходимости удерживать кнопку мыши нажатой при перемещении от точки к точке. Просто щелкните, чтобы добавить точку, отпустите кнопку мыши, перейдите к следующему месту, где линия должна изменить направление, затем щелкните, чтобы добавить новую точку: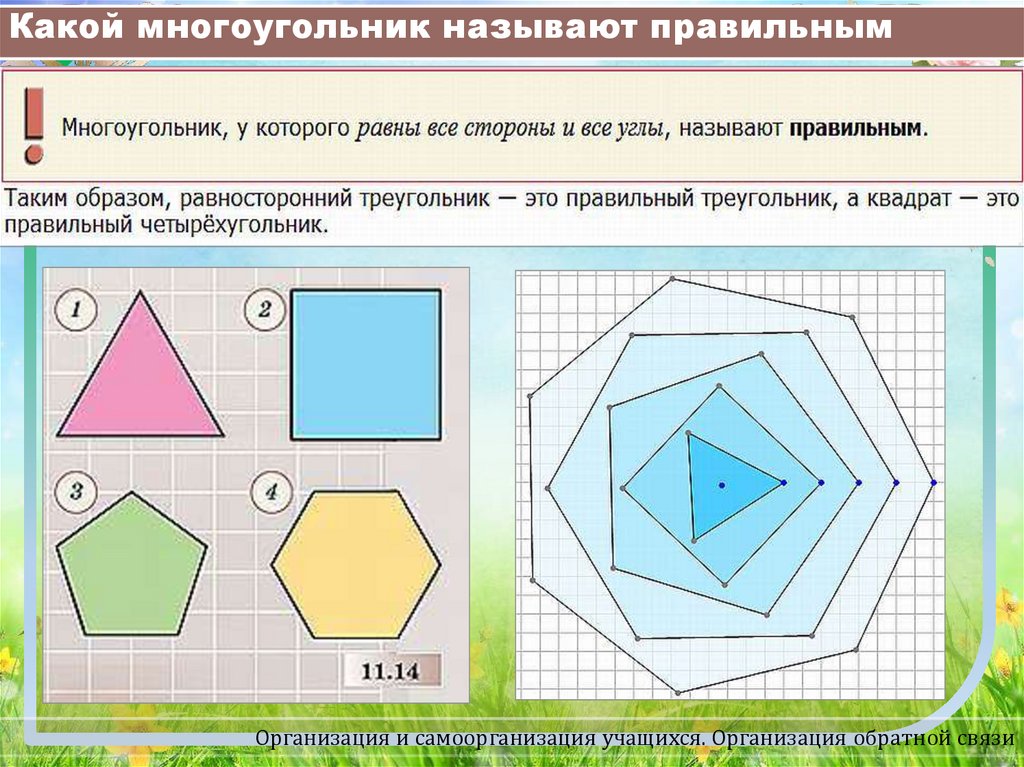 Photoshop автоматически закроет выделение прямой линией от точки, на которой вы щелкнули, до начальной точки.
Photoshop автоматически закроет выделение прямой линией от точки, на которой вы щелкнули, до начальной точки.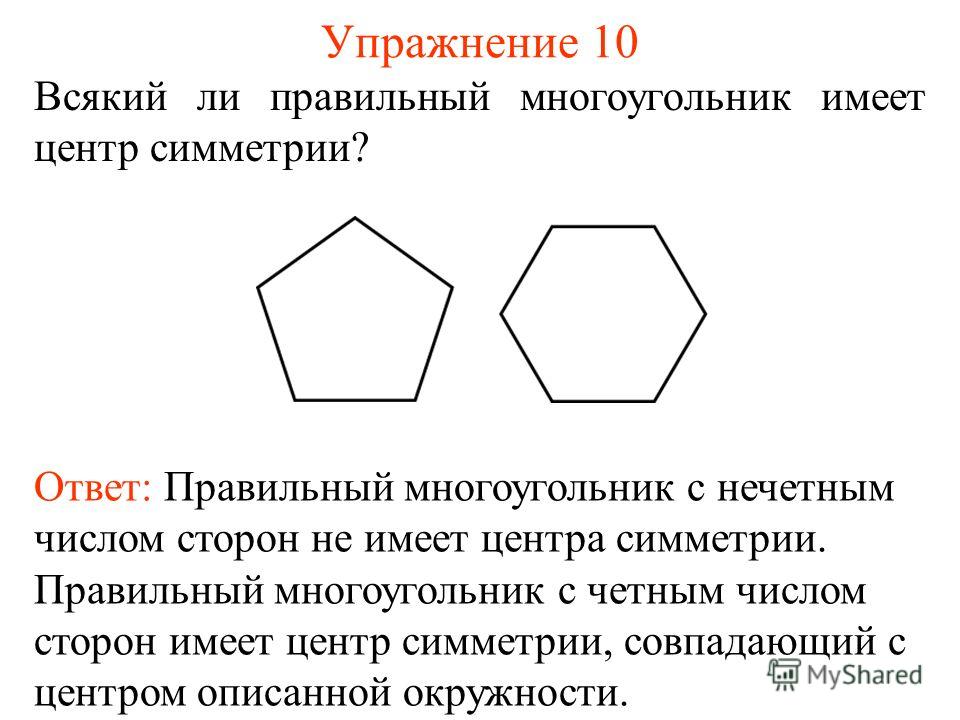 выбирая это.
выбирая это.
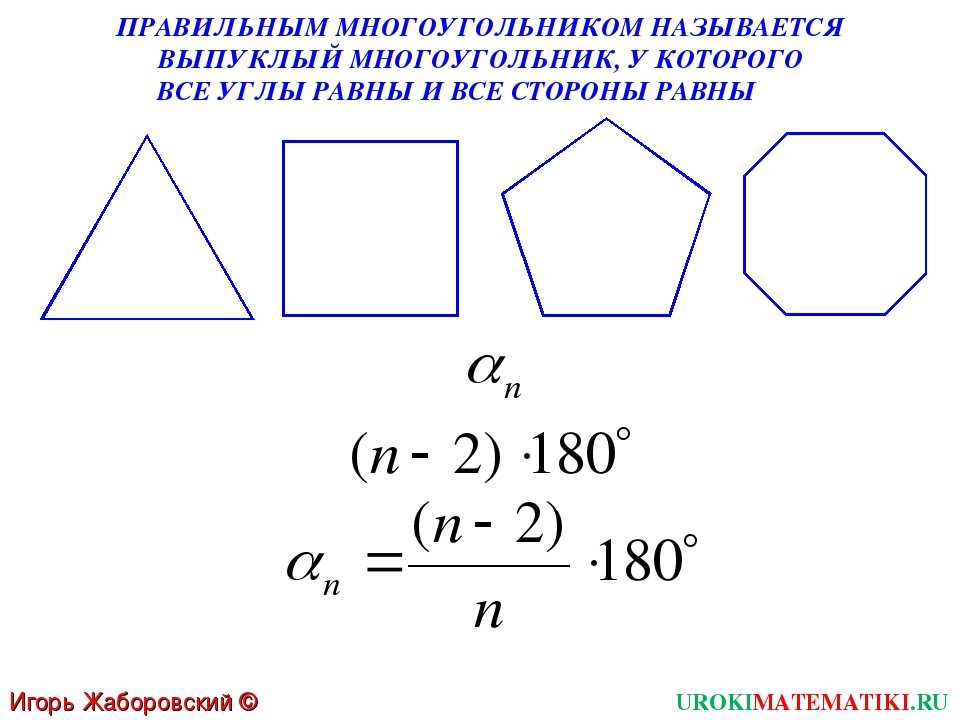 Чтобы добавить изображение на рекламный щит, я вернусь к своей исходной фотографии, затем перейду в меню Edit вверху экрана и выберу команду Paste Into :
Чтобы добавить изображение на рекламный щит, я вернусь к своей исходной фотографии, затем перейду в меню Edit вверху экрана и выберу команду Paste Into :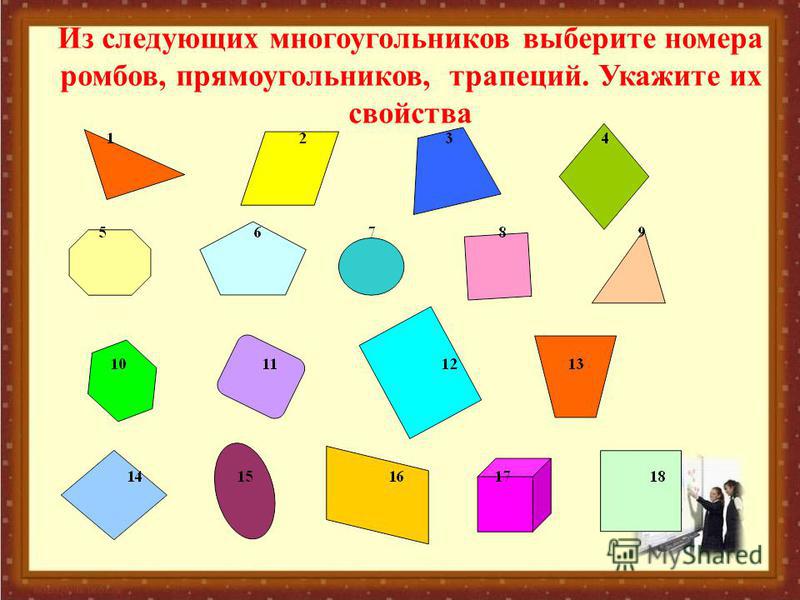 Просто щелкните, чтобы добавить точки вдоль объекта в те места, где контур выделения должен изменить направление, затем щелкните обратно в начальной начальной точке, чтобы завершить выделение.
Просто щелкните, чтобы добавить точки вдоль объекта в те места, где контур выделения должен изменить направление, затем щелкните обратно в начальной начальной точке, чтобы завершить выделение.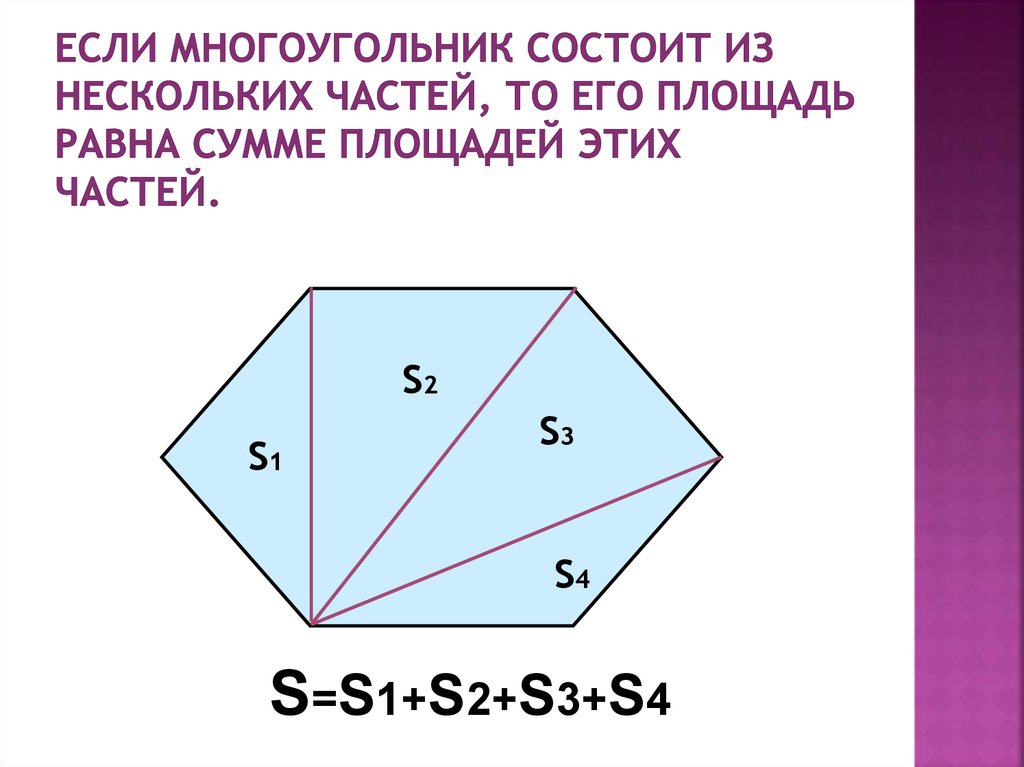 Отпустите клавишу пробела, чтобы вернуться к инструменту «Многоугольное лассо»:
Отпустите клавишу пробела, чтобы вернуться к инструменту «Многоугольное лассо»: 
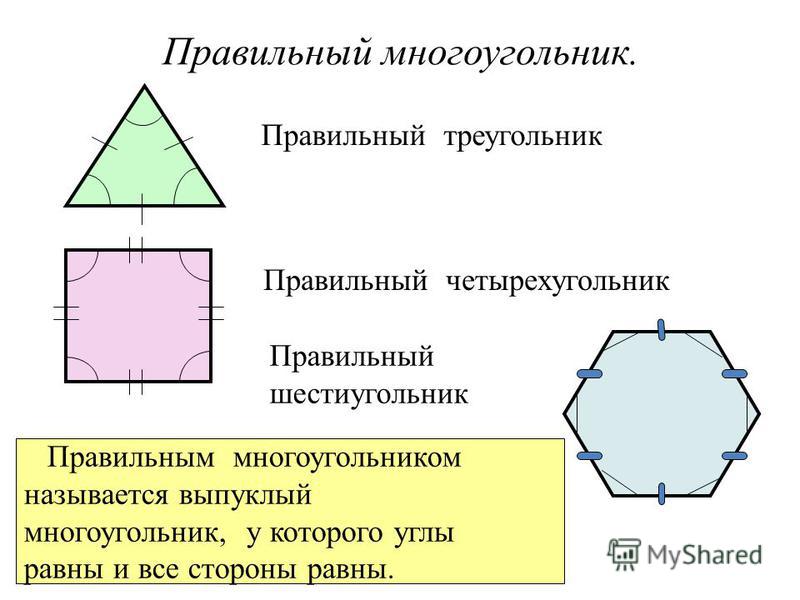
 (выбранная область) и оставить здание (невыделенную область) видимым:
(выбранная область) и оставить здание (невыделенную область) видимым:
 Затем мы применяем фильтр «Среднее», который показывает среднее значение для всех цветов в выделенной области, как если бы они смешивались в большом горшке. Затем мы просто повторяем этот процесс, пока он не закончится.
Затем мы применяем фильтр «Среднее», который показывает среднее значение для всех цветов в выделенной области, как если бы они смешивались в большом горшке. Затем мы просто повторяем этот процесс, пока он не закончится. Назовите действие, назначьте функциональную клавишу и нажмите «Запись».
Назовите действие, назначьте функциональную клавишу и нажмите «Запись». Backspace удаляет предыдущую точку.
Backspace удаляет предыдущую точку. Щелкните правой кнопкой мыши> Копировать стиль слоя, щелкните верхний и нижний треугольные слои, удерживая клавишу Shift, щелкните правой кнопкой мыши> Вставить стиль слоя.
Щелкните правой кнопкой мыши> Копировать стиль слоя, щелкните верхний и нижний треугольные слои, удерживая клавишу Shift, щелкните правой кнопкой мыши> Вставить стиль слоя. Цель состоит в том, чтобы получить изображение , представленное как набор перекрывающихся многоугольников различных цветов и прозрачностей .
Цель состоит в том, чтобы получить изображение , представленное как набор перекрывающихся многоугольников различных цветов и прозрачностей .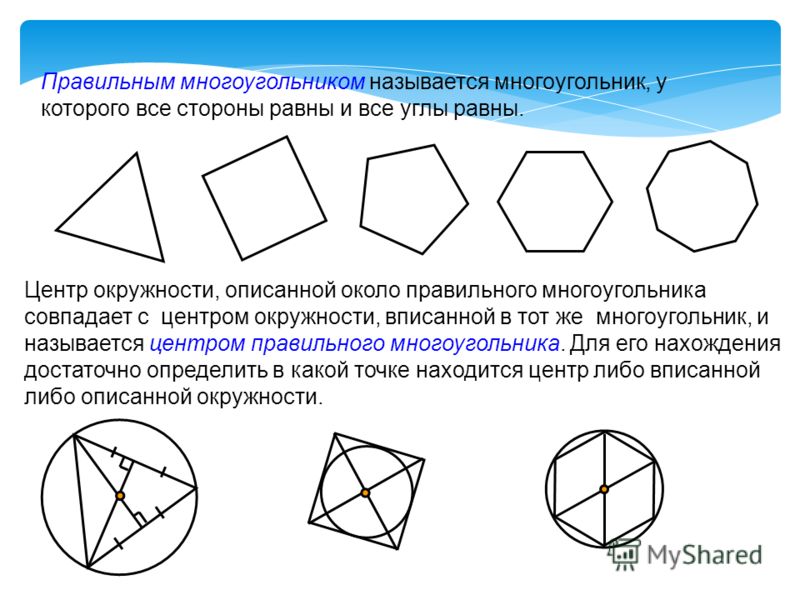 74% фитнес
74% фитнес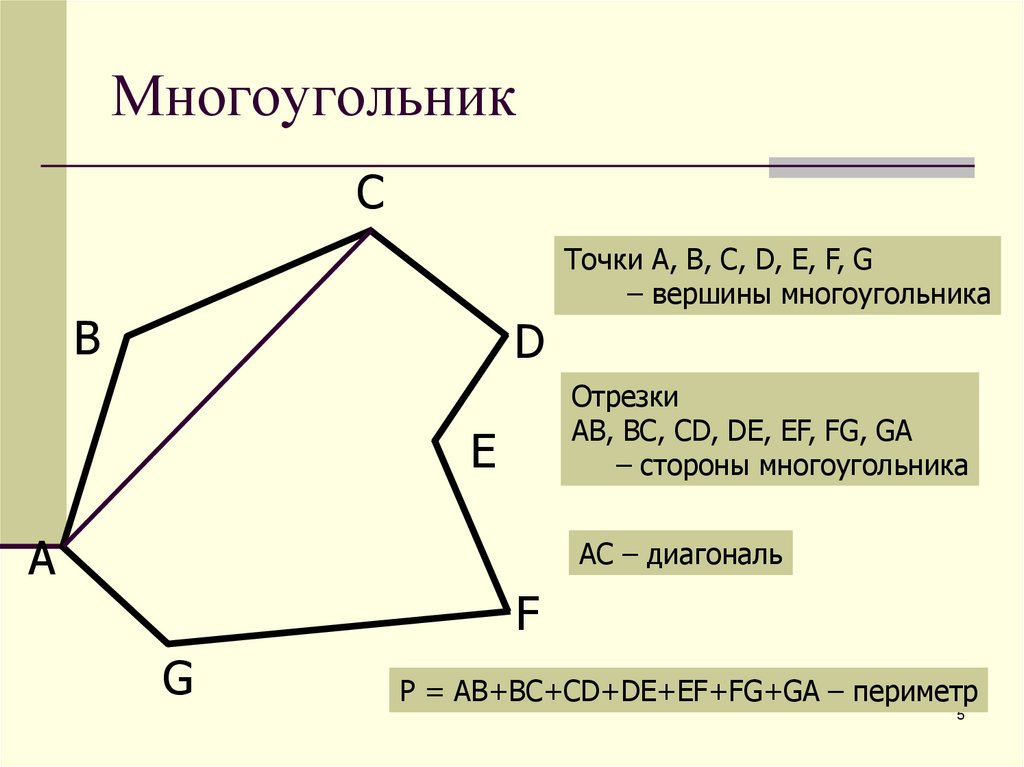 36% фитнес
36% фитнес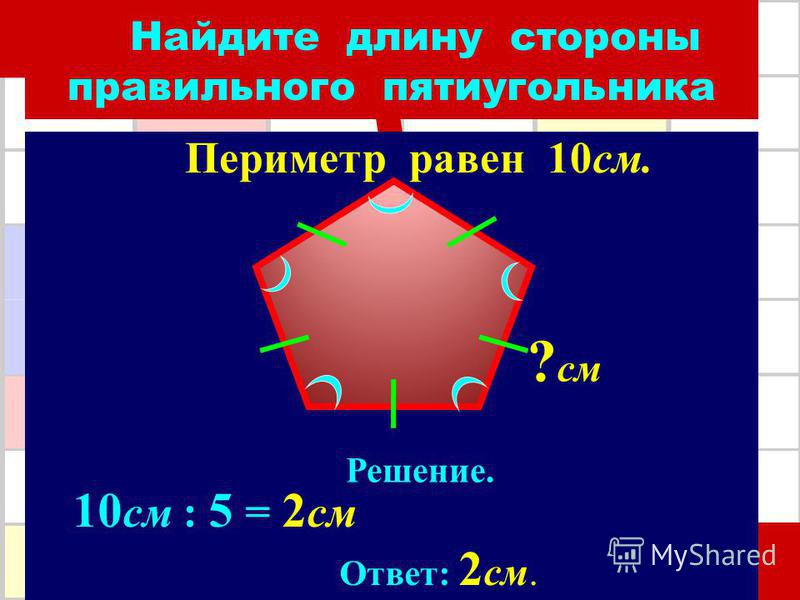
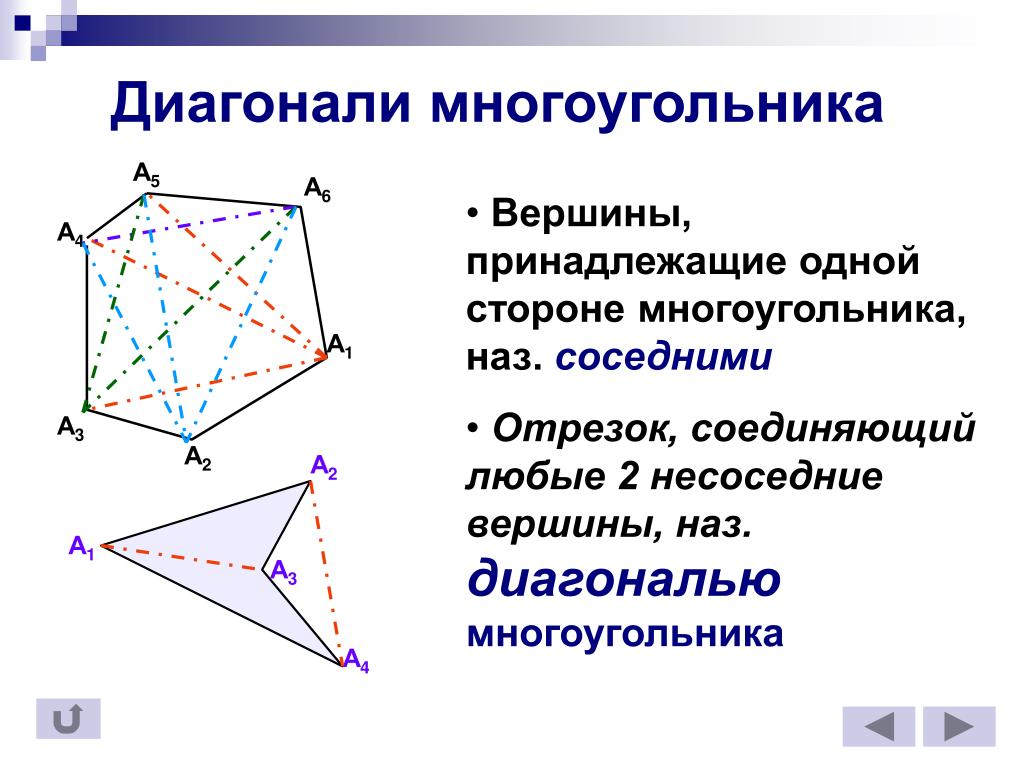 14% фитнес
14% фитнес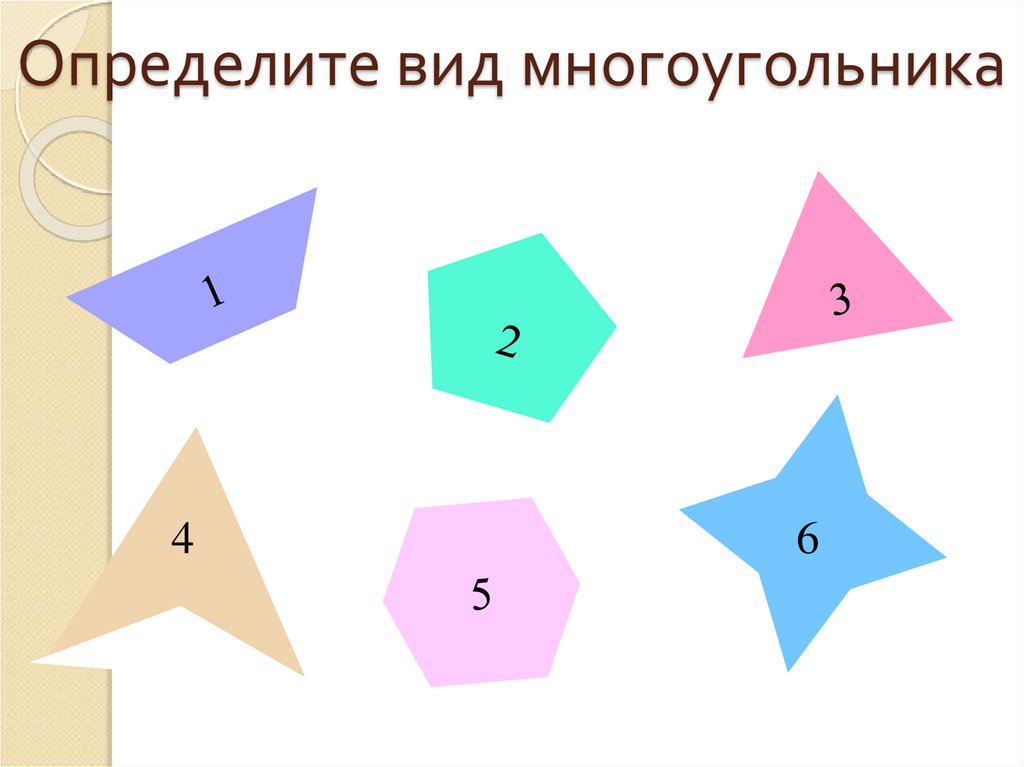 95.01%, макс 99,08%, среднее 96,59%, медиана 96,65%
95.01%, макс 99,08%, среднее 96,59%, медиана 96,65%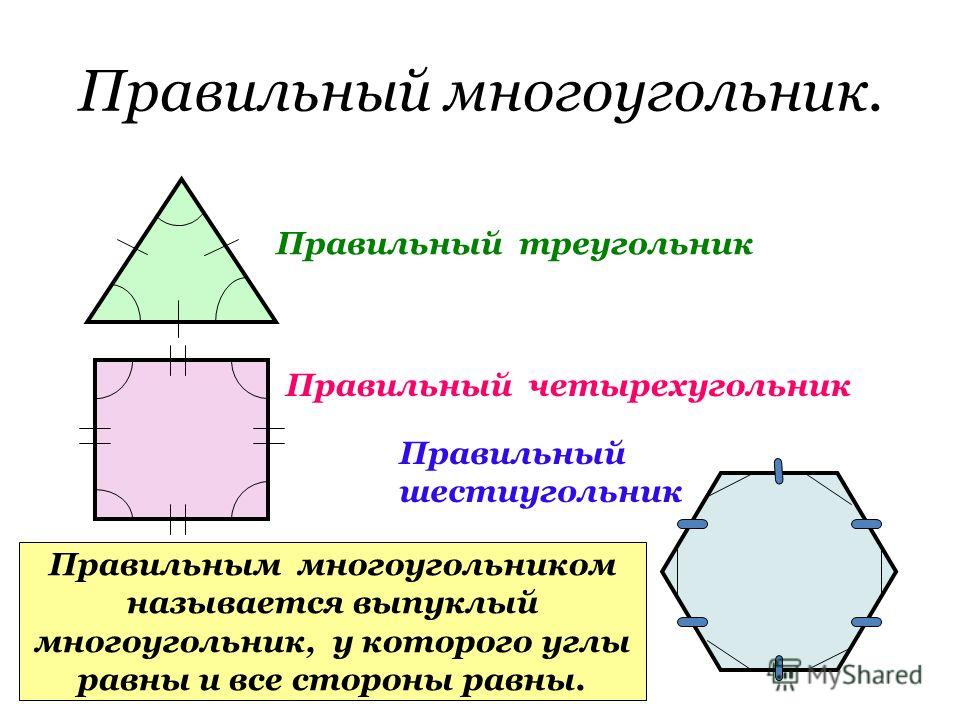 Большинство ошибок должны быть исправлены сейчас.
Большинство ошибок должны быть исправлены сейчас. .. XN YN ... R G B АЛЬФА X0 Y0 X1 Y1 ... XN YN ...
.. XN YN ... R G B АЛЬФА X0 Y0 X1 Y1 ... XN YN ... 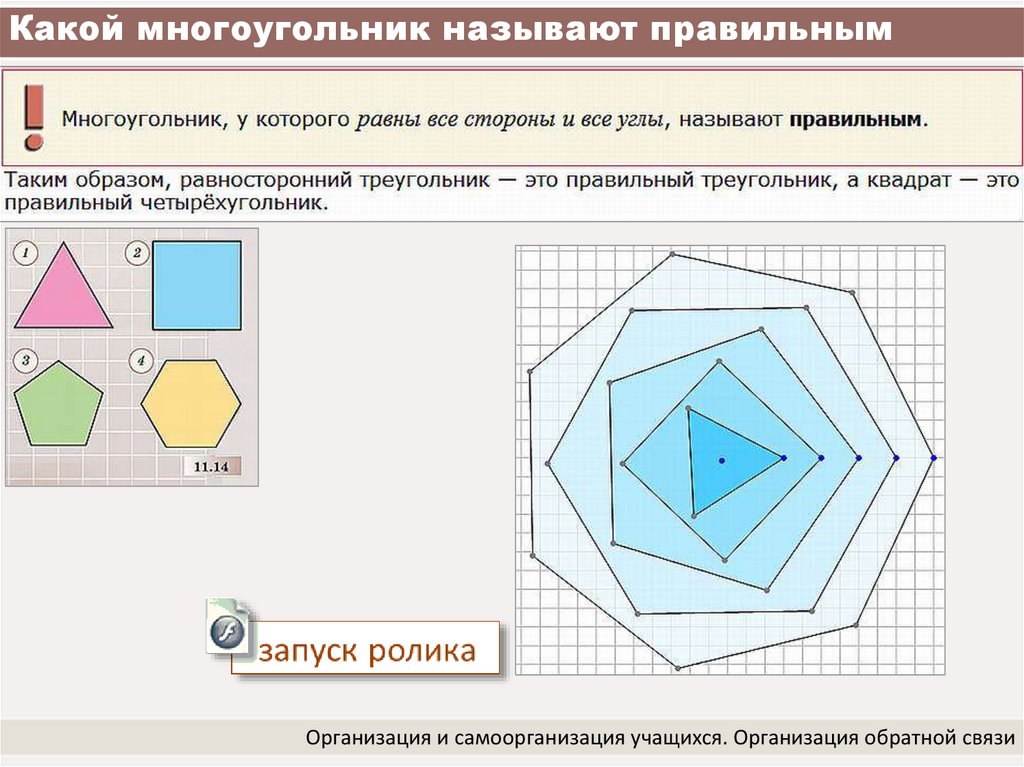
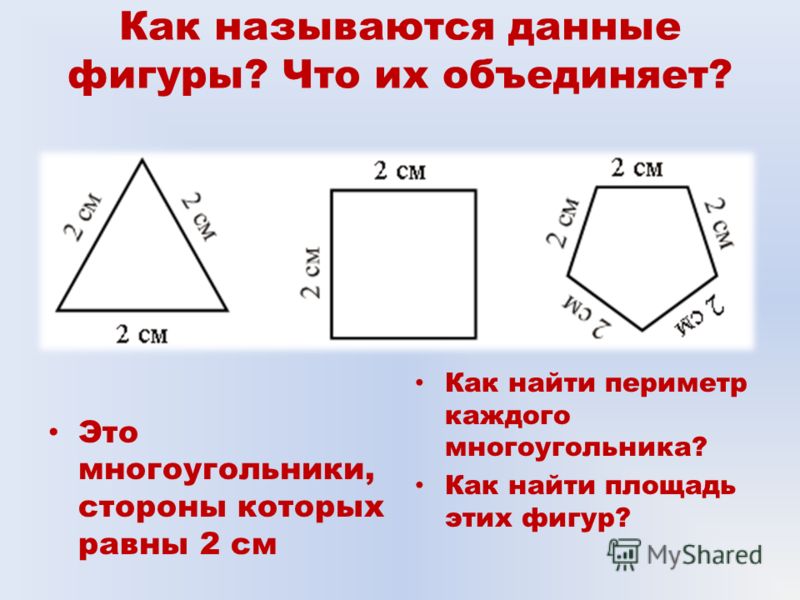 Чтобы применить изменения, которые вы выбрали для ортофотоплана: вы должны обновить ортофотоплан после назначения изображений в выбранной области. Нажмите кнопку Обновить ортофотоплан . Эта кнопка будет выделена только после того, как вы назначили изображения.(Рисунок 4)
Чтобы применить изменения, которые вы выбрали для ортофотоплана: вы должны обновить ортофотоплан после назначения изображений в выбранной области. Нажмите кнопку Обновить ортофотоплан . Эта кнопка будет выделена только после того, как вы назначили изображения.(Рисунок 4)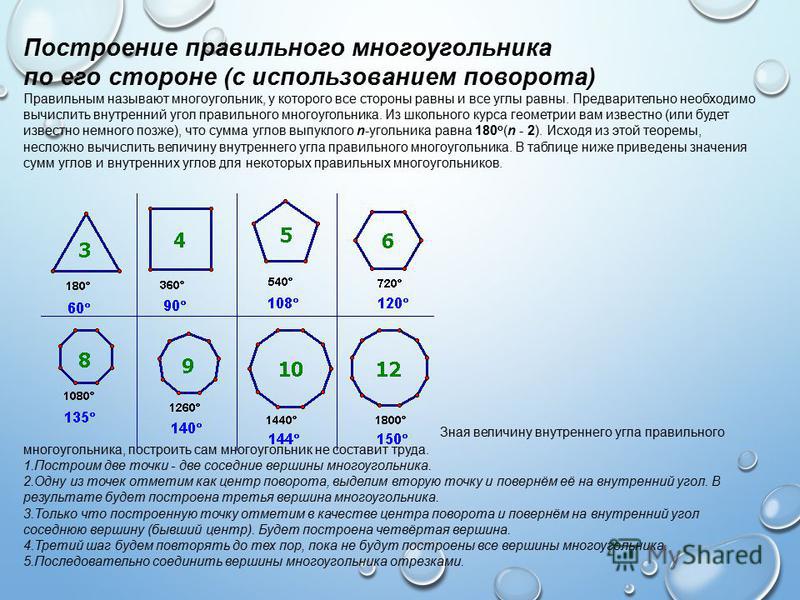
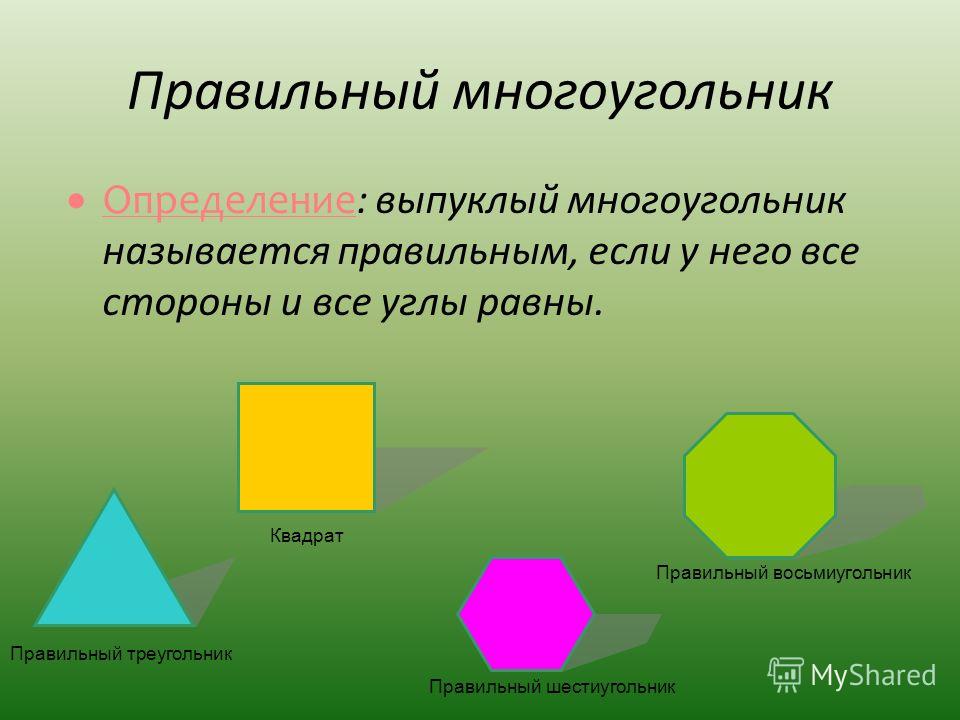
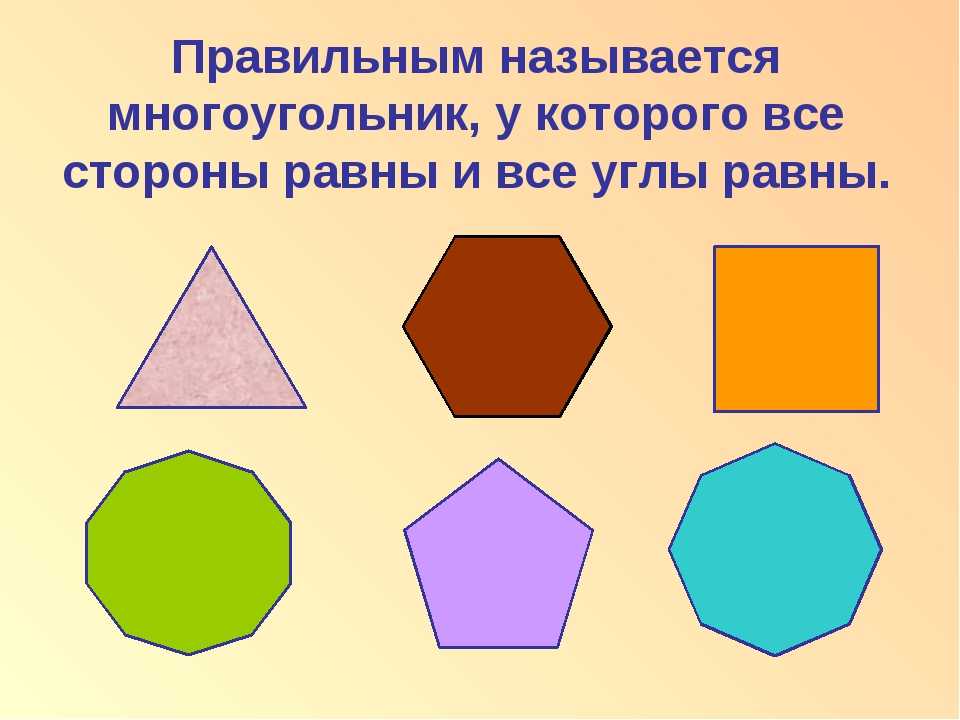

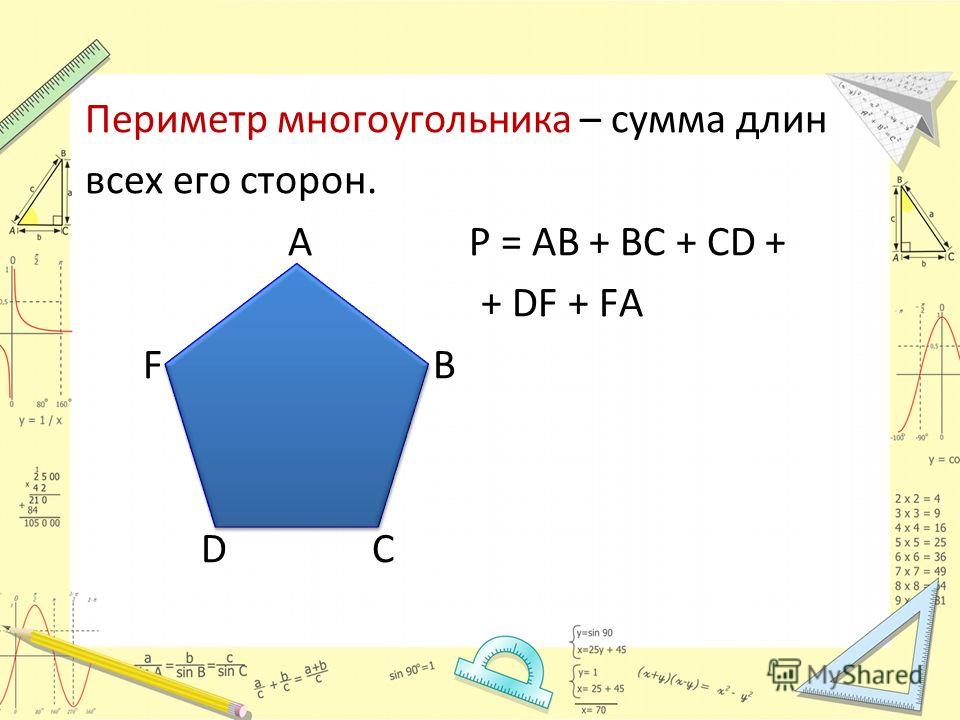
 5
5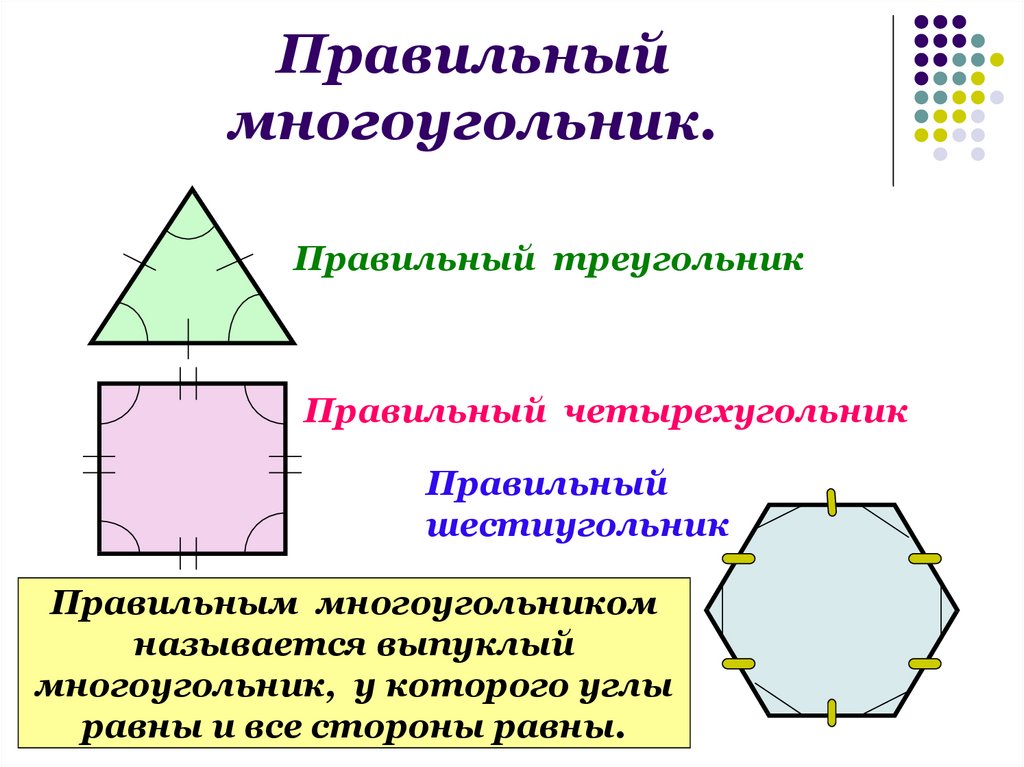
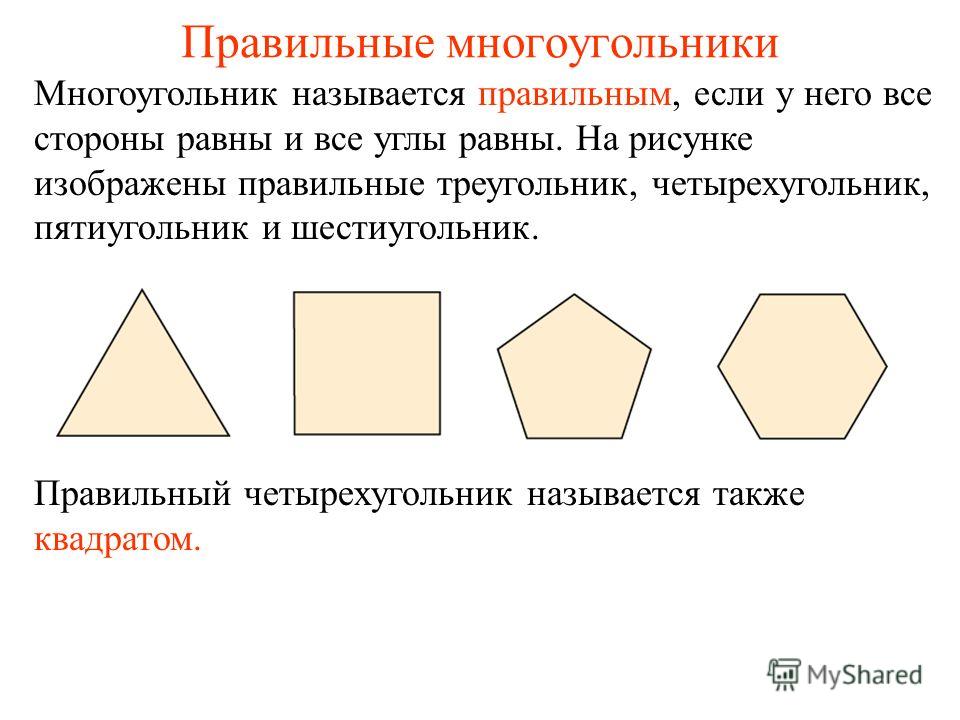 Так, в невыпуклом пятиугольнике, изображенном на рис.3, два угла прямые, два угла имеют по 45°, а один содержит 270°. Суммаа углов составляет 180° (5-2)=540°.
Так, в невыпуклом пятиугольнике, изображенном на рис.3, два угла прямые, два угла имеют по 45°, а один содержит 270°. Суммаа углов составляет 180° (5-2)=540°. 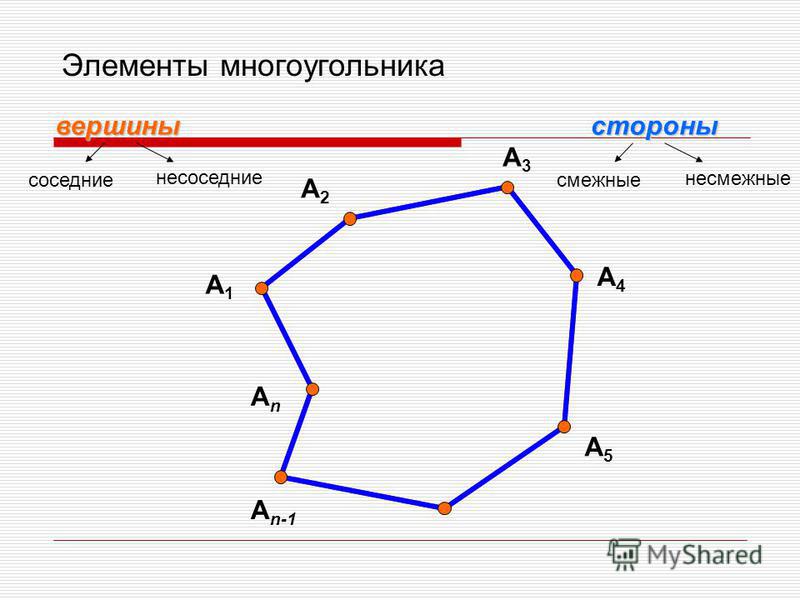 Нажмите на инструмент «Выбор произвольной формы», если хотите создать неправильную форму.
Нажмите на инструмент «Выбор произвольной формы», если хотите создать неправильную форму. Нажмите «Контур» в группе «Фигуры». Нажмите «Нет плана». Нажмите «Цвет 2» в группе «Цвета» и выберите белый (или любой другой цвет фона, который вы хотите использовать) в качестве цвета заливки. Форма, которую вы только что создали, должна появиться, чтобы обрезать фотографию под другим углом.
Нажмите «Контур» в группе «Фигуры». Нажмите «Нет плана». Нажмите «Цвет 2» в группе «Цвета» и выберите белый (или любой другой цвет фона, который вы хотите использовать) в качестве цвета заливки. Форма, которую вы только что создали, должна появиться, чтобы обрезать фотографию под другим углом.