Многоугольники фото 2 класс: стороны, вершины, диагонали. Периметр многоугольника

Многоугольники 2 класс — математика, уроки

Тема: Многоугольники.2 класс

Задачи урока:

• ввести понятие “Многоугольник”, научить находить и показывать вершины, стороны и углы многоугольника, рассмотреть обозначение многоугольника латинскими буквами;

• совершенствовать навыки решения задач; развивать устные вычислительные навыки, логическое мышление;

• обогащать кругозор обучающихся, прививать интерес к предмету, воспитывать чувство дружбы и взаимопомощи.

Оборудование:

• учебник “Математика” В.Н.Рудницкая, 2 класс,

• таблицы” Многоугольники”, “Меры длины”,

• индивидуальные карточки,

• примеры для игры на кленовых листочках,

• плакат “Овощи и фрукты”,

• набор муляжей — овощи и фрукты,

I. Организационный этап

Придумано кем-то
Просто и мудро
При встрече здороваться
— Доброе утро! —
Солнцу и птицам.
— Доброе утро! —
Улыбчивым лицам.
И каждый становится
Добрым, доверчивым.
Доброе утро длится до вечера.

В.Кривошеев “Доброе утро”

Сегодня урок необычный у нас.
Готов к нему вижу каждый из вас:
Улыбка, уверенность. Что ж: “Так держать!”
За парты садитесь, пора начинать.

(Звучит мелодия для релаксации)

Улыбнитесь друг другу. Сядьте удобно. Расслабьте лоб, брови, опустите веки. Расслабьте щеки, губы, мышцы шеи, плечи, кисти рук, ноги, пальцы ног. Ваши руки и ноги теплеют. Дыхание становится свободное, спокойное, ровное.

Вы на лесной поляне, ярко светит солнце. Весело щебечут птицы. Легкий ветерок развевает ваши волосы. У вас прекрасное настроение. Вы можете выполнить любое трудное задание. Я буду считать до пяти. Когда я скажу “пять”, вы откроете глаза: 1, 2, 3, 4, 5.

II. Устный счет

— О каком времени года пойдет речь?

Несу я урожаи,
Поя вновь засеваю.
Птиц к югу отправляю,
Деревья раздеваю,
Но не касаюсь елочек и сосен
Я… (осень)

(Просмотр отрывка из видеоролика “Краски осени”)

1.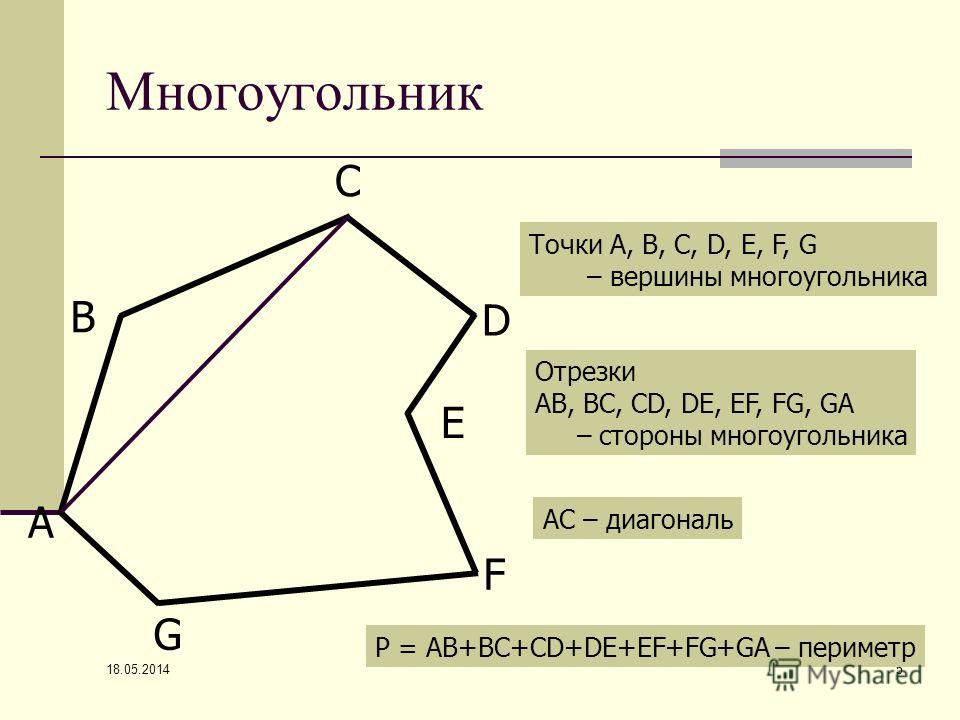 Игра “Собери листья”

На доске запись:

9+9	7+7
15-6	16-9
16-8	12-7
7+5	7+6

12, 7, 5, 18, 14, 9, 8, 13

(Оответы в примерах соответствуют определенной букве, собрав которые получается слово “Сентябрь”)

Этот месяц — самый прекрасный,
Появляется лист первый красный;
Остывает немного земля,
Урожай украшает поля.
Младших — мамы за руки ведут,
Воздух будто наполнен добром,
Этот месяц зовут сентябрем.

— Какие народные приметы знаете о сентябре?

— На какие две группы можно разбить эти числа?

12, 7, 5, 18, 14, 9, 8, 13

(Однозначные и двузначные)

2. Работа 1 группы обучающихся по индивидуальным карточкам, 2 группа — работают по электронному пособию “Математический тренажер”.

На уроке интересно,
Дети все решают вместе.
Чтобы нам умнее стать,
Мы готовы посчитать.

3. Счет от 10 до 100 цепочкой в прямом и обратном порядке

— Как называются компоненты при сложении? Вычитании?

— Как узнать, на сколько одно число больше или меньше другого?

— Чему равна сумма чисел 20 и 10? 30 и 20?

— Чуму равна разность чисел 80 и 60? 50 и 10?

— На сколько 40 больше чем 10?

— Назовите число, которое состоит из 3 десятков и 5 единиц, 8 десятков и 2 единиц?

4. Считалка “Шла бабка с Загорья”

Несла кузовок.
В том кузовочке лежали грибочки.
Кому-гриб,
Кому-два,
А тебе, дитятко,
Весь кузовок.

(Кто вышел из игры, тот придумывает задачу про грибы)

5. Составление задач по схеме. (На доске панно “Корзина и грибочки”)

Осень – славная пора!
Любит осень детвора.
Сливы, груши, виноград,
Все поспело для ребят.

6. Игра “Найди лишний предмет”

Крыжовник, малина, вишня, клубника, яблоко (на доске иллюстрации).

Рассказ о пользе витаминов.

7. Нарисуйте недостающую фигуру, чтобы в каждом ряду были фигуры разной формы.

(Выполнение работы на карточках. Самопроверка с доски)

8. Сказочные задачи

— Крош сначала съел 8 морковок, а затем 9. Сколько всего морковок съел Крош?

— Из первого улья медвежонок собрал 10 кг меда, из второго — 5 кг, а из третьего — столько, сколько из первого и второго вместе. Сколько килограммов меда собрал медвежонок из третьего улья?

Физминутка

Косолапый мишка встал,
Присел, поднялся,
На носочках покачался.
Потом кругом пошел,
Красну ягодку нашел,
Съел и сел.

III. Введение в тему урока

Где играют дружно,
Считают умело,
Там и сказке можно
Появиться смело.
Жил-был на свете медвежонок. (Cлайд 2-15. Презентация у автора)

(Он поможет нам открыть новые знания о геометрических фигурах)

IV. Постановка проблемы

— Какую фигуру можно сложить из трех палочек? (Треугольник)

— Давайте разомнем наши пальчики перед практической работой.

Вот помощники мои.
Их как хочешь, поверни.
По дороге белой, гладкой,
Скачут пальцы как лошадки.
Чок — чок-чок-чок.
Скачет резвый табунок.

V. Открытие новых знаний”. Практическая работа

1. Возьмите в руки листочек. Поставим 3 точки в разных местах. Сгибаем лист так, чтобы линия сгиба проходила через каждые две точки. Соединим линейкой все точки. Вырезаем фигуру. Какая фигура получилась? Сколько поставили точек? Это вершины треугольника. Покажите стороны треугольника. Сколько их? Сколько углов?

Рассмотрите чертежи на доске.

2. Покажите четырехугольник. Его стороны, вершины, углы. Дайте название этой фигуре. {Четырехугольник). Расскажите о пятиугольнике.

— Какое название дадим этой фигуре? (Шестиугольник)

— Можно ли к этим фигурам добавить круг? (Нет, нет углов)

— Какое название дадим всем фигурам с углами? Как их можно назвать, одним словом. (Многоугольники)

— Какую закономерность вы обнаружили? (У каждой следующей фигуры увеличивается количество углов и сторон на 1)

(Молодцы! Возьмите мой солнечный луч!) Слайд 16

Физминутка для глаз. (Песенка Кота Леопольда). Слайд 17–19

Помоги нам, месяц ясный, спаси волшебный лес от чудища. Помогу, только выполните задания учебника.

VI. Работа по учебнику

1. С. 36, №1.

— Рассмотрите печенье. Сколько углов имеет каждая из фигур? Теперь рассмотрите желтый многоугольник. Сколько в нем углов?

— Какой фигурой является каждая сторона многоугольника? (Отрезком). Сколько сторон у желтого многоугольника?

— Какой фигурой является вершина многоугольника? (Точкой)

— Сколько вершин имеет желтый многоугольник? (Пять)

Вывод: В желтом многоугольнике 5 углов, 5 сторон, 5 вершин.

VII. Работа с рубрикой “Обрати внимание!” (чтение правила)

В любом многоугольнике одно и тоже количество углов, сторон и вершин.

— Сколько же углов в семиугольнике?

— Сколько углов в десятиугольнике?

— Сколько сторон в пятнадцатиугольнике?

На доске: плакат “14-тиугольник”.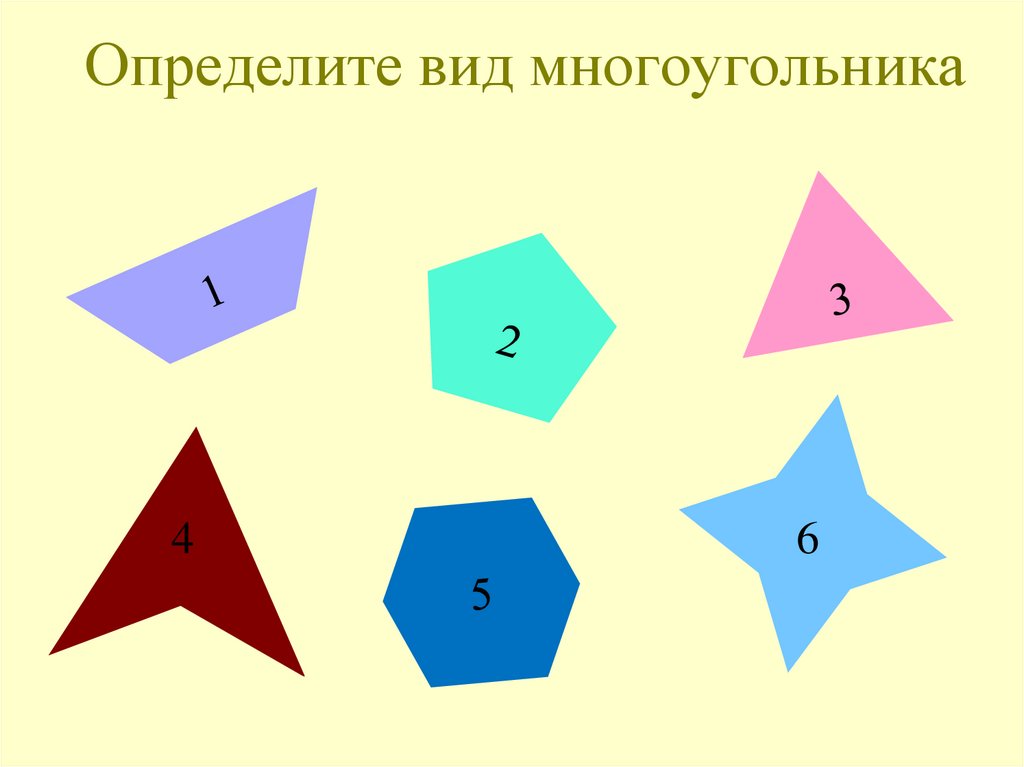

— Как определить название этого многоугольника? Что проще всего считать? (Вершины)

А теперь попробуйте ответить на более сложные вопросы: бывают ли одноугольники? Двуугольники?

— Как называется многоугольник, у которого 100 вершин?

VIII. Знакомство с показом элементов многоугольника

— Давайте научимся показывать элементы многоугольника: вершины, стороны, углы. (На доске — рисунок треугольника)

Вершины — это точки. (Указкой показать каждую точку треугольника)

Теперь покажем стороны. Сторона многоугольника — это какая фигура? (Отрезок) Показываем стороны как отрезки. (Конец указки движется от вершины, далее по отрезку до другой вершины)

Углы будем показывать вращением указки. Один конец указки должен находиться в вершине треугольника, сама указка — вдоль стороны, выходящей из этой вершины. Далее, не отрывая указки от вершины угла, двигаем указку по направлению к другой стороне, пока указка не совместится с этой стороной. (Продемонстрировать обучающимся, как это правильно делать)

— Вершины треугольника обозначают буквами. Читать обозначения можно разными способами, начиная с любой вершины. (Например: треугольник АВС, АСВ и т.д.)

2. Работа по учебнику

С.37, №2.

— Что изображено на рисунке? (Многоугольники)

— Как называются данные многоугольники? (Треугольник, пятиугольник)

— Какими геометрическими фигурами являются вершины и стороны многоугольника? (Это точки и отрезки)

— Как принято обозначать точки на чертеже? (Прописной буквой латинского алфавита)

— А отрезки? (Двумя прописными буквами латинского алфавита)

— Найдите вершины треугольника. (О, М, К)

— Найдите стороны треугольника. (МО, МК, ОК)

— Сколько вершин и сторон у этой фигуры?

Вот вам звездная пыль. Слайд 20

Физминутка для глаз. (Звезды). Слайды 21

Помоги нам ,Дюймовочка, спаси наш лес от чудища.

— Конечно помогу, только вы покажите, как вы умеете работать в тетрадях. Слайды 22-23

IX. Работа тетради №1

1. Задание № 50 стр. 16. Закрасьте только многоугольники.

2. Задание.№ 51 стр. 16.

Отметьте вершины многоугольников красным карандашом.

Стороны многоугольников синим карандашом. (Самопроверка с доски)

3. Задание № 49 с. 16. — Прочитайте задачу.

— Что вам известно? Что требуется узнать?

— Какая схема нужна для записи условия задачи? Запишите решение задачи самостоятельно. Проверка в парах. (Показ сигнальными кругами)

Спасибо вам, дорогие ребята. Я дарю вам волшебную розу. Бегите, спасайте свой лес. Слайд 24-29

X. Применение новых знаний на практике

Недавно мы поздравляли Сашу с Днем рождения. Посмотрите внимательно на фото. Слайд 30

— Какой геометрической фигурой можно назвать торт, которым нас угощал Саша? (Квадрат, многоугольник)

— Сколько у квадрата углов, сторон, вершин?

1. Это интересно! Слайд 31

Пирамида Хеопса.

— Перед вами — одно из семи чудес света — Пирамида Хеопса. Это крупнейшая из египетских пирамид, единственное из “Семи чудес света”, сохранившееся до наших дней. В основании пирамиды — квадрат. Вы узнаете о ней много интересного на уроках истории в старших классах.

XI. Домашнее задание

Выполнить аппликацию из многоугольников.

1 класс, 2 класс (круг, овал, квадрат, треугольник и многоугольник)

Рисунок из геометрических фигур — это задание для детей дошкольного и младшего школьного возраста, позволяющее развить пространственное воображение, знание геометрических фигур и улучшить моторные навыки черчения.

Для вашего удобства мы сделали рисунки-раскраски из геометрических фигур, которые можно распечатать и раскрасить (для дошкольников). После каждой раскраски представлен пример рисунка на эту же тему. Рисунок дети выполняют самостоятельно по линейке и раскрашивают красками или карандашами (для школьников). Раскраски и рисунки выполнены на следующие темы:

• «Воздушный транспорт»
• «Игрушки»
• Животные из геометрических фигур «Кошка и мышка»
• «Транспорт»
• «Домик в деревне»
• «Море и корабль»
• «Железная дорога»
• «Лесная новогодняя сказка»
• «Летняя поляна»
• «Космический полет»

Рисунки из геометрических фигур для детей — план занятия

• Начните занятие с того, что выясните какие геометрические фигуры помнит ребенок. Он должен уверенно называть и видеть круг (полукруг), овал, квадрат, треугольник и многоугольник . Дети постарше смогут увидеть в рисунках ломаную линию.
• Найдите геометрические фигуры на рисунке. Чем больше ребенок найдет геометрических фигур — тем лучше. Можно их посчитать.
• Заполните цветом раскраску или нарисуйте и выбранную композицию. Очень хорошо, если ребенок пойдет дальше и нарисует свои элементы рисунка.

Композиция из геометрических фигур рисунок «Воздушный транспорт»

Рисунок из геометрических фигур 1 класс — воздушный транспорт. Самолет, воздушный шар и вертолет вызовут интерес у мальчиков. Можно рассказать интересные факты об устройстве транспорта, его скорости, истории создания и роли в наши дни.

Раскраска «Воздушный транспорт из геометрических фигур»Рисунок «Воздушный транспорт из геометрических фигур»

Рисунок из геометрических фигур «Игрушки»

Тема игрушек подойдет для самых маленьких художников. Сюда можно нарисовать любимого мишку или зайчика, выполнив его из геометрических фигур.

Раскраска «Игрушки из геометрических фигур»Рисунок «Игрушки из геометрических фигур»

Животные из геометрических фигур рисунки — «Кошка и мышка»

Самый любимый сюжет — война кошки и мышки.

Раскраска из геометрических фигур»Кошка и мышка»Рисунок из геометрических фигур»Кошка и мышка»

Рисунок из геометрических фигур «Транспорт»

Рисуя транспорт можно повторить его виды и предназначение.

Раскраска из геометрических фигур»Транспорт»Рисунок из геометрических фигур»Транспорт»

Рисунок из геометрических фигур»Домик в деревне»

Нежный яркий рисунок с уточками и домиком понравиться всем.

Раскраска из геометрических фигур»Домик в деревне»Рисунок из геометрических фигур»Домик в деревне»

Рисунок из геометрических фигур»Море и корабль»

Дети обожают рисовать море, рыбок и других морских жителей.

Раскраска из геометрических фигур»Море и корабль»Рисунок из геометрических фигур»Море и корабль»

Рисунок из геометрических фигур»Железная дорога»

Раскраска из геометрических фигур»Железная дорога»Рисунок из геометрических фигур»Железная дорога»

Рисунок из геометрических фигур «Лесная новогодняя сказка»

Раскраска из геометрических фигур»Лесная новогодняя сказка»Рисунок из геометрических фигур»Лесная новогодняя сказка»

Рисунок из геометрических фигур»Летняя поляна»

Любимый сюжет — лето, поляна, цветы и различные насекомые.

Раскраска из геометрических фигур»Летняя поляна»Рисунок из геометрических фигур»Летняя поляна»

Рисунок из геометрических фигур»Космический полет»

Раскраска из геометрических фигур»Космический полет»Рисунок из геометрических фигур»Космический полет»

Рисунки из геометрических фигур (подборка из интернета)

Раскраска из геометрических фигур «Петушок»Рисунок из геометрических фигур «Петушок»Раскраска из геометрических фигур «Домик»Рисунок из геометрических фигур «Домик»Раскраска из геометрических фигур «Робот-солдат»Рисунок из геометрических фигур «Робот-солдат»Раскраска из геометрических фигур «Цветок»Рисунок из геометрических фигур «Цветок»Пчелка из геометрических фигурРаскраска из геометрических фигур «Солнечная улица»

Рисунки из геометрических фигур (видео)

Картинки из геометрических фигур:

Рисунок из геометрических фигур «Домик»:

Аппликации из геометрических фигур 1 класс:

Аппликации тренируют моторику, ведь каждую деталь надо вырезать ножницами. Аппликации помогут научиться представлять целое и его части, помогут не только вспомнить фигуры, но и ощутить их руками.

Рисунки из геометрических фигур (идеи из интернета)

Рисунок «ракета»Ракета из овалов, башня из квадратов, ракета из треугольников, человечек из квадратов, человечек из треугольников, человечек из овалов

Что такое многоугольник? Форма, типы, формулы, примеры, факты

Что такое многоугольник?

В геометрии многоугольник можно определить как плоскую или плоскую двумерную замкнутую форму, ограниченную прямыми сторонами. У него нет изогнутых сторон. Стороны многоугольника также называются его ребрами. Точки, где встречаются две стороны, являются вершинами (или углами) многоугольника.

Вот несколько примеров полигонов.

Вот несколько не-примеров многоугольника

Диаграмма многоугольников

Многоугольники именуются на основе количества их сторон. Многоугольники обычно обозначаются n-угольником, где n представляет количество сторон, которые он имеет. Например, пятиугольник называется 5-угольником, десятиугольник называется 10-угольником и так далее.

Однако несколько полигонов имеют специальные имена. Минимальное количество сторон, которое может иметь многоугольник, равно 3, потому что ему нужно как минимум 3 стороны, чтобы быть замкнутой формой, иначе он будет открытым.

Несмотря на то, что многоугольники со сторонами больше 10 также имеют специальные имена, мы обычно обозначаем их n-угольником, так как имена сложные и непростые для запоминания.

Типы многоугольников

Многоугольники можно классифицировать на основе количества их сторон и углов:

1. Классификация на основе сторон: Правильные и неправильные многоугольники:

90 007 Правильные–0 многоугольники Многоугольники, имеющие равные стороны и углы, являются правильными многоугольниками.

Например, равносторонний треугольник — это трехсторонний правильный многоугольник. Квадрат – это правильный четырехугольник. Правильный шестиугольник – это правильный шестиугольник.

Вот несколько примеров правильных многоугольников.

Неправильные многоугольники  – Многоугольники с неравными сторонами и углами являются неправильными многоугольниками.

Вот несколько примеров неправильных многоугольников.

2. Классификация по углам: Выпуклые и вогнутые Многоугольники:

Выпуклые многоугольники — Выпуклый многоугольник — это многоугольник, все внутренние углы которого меньше 180°.

В выпуклых многоугольниках все диагонали находятся внутри многоугольника.

( Диагональ — это отрезок, соединяющий любые две непоследовательные вершины многоугольника )

Вот несколько примеров выпуклых многоугольников.

Вогнутые многоугольники — Вогнутый многоугольник — это многоугольник, у которого хотя бы один внутренний угол больше 180°.

В вогнутых многоугольниках не все диагонали находятся внутри многоугольника.

Вот несколько примеров вогнутых многоугольников.

Разница между выпуклым и вогнутым многоугольником

3. Простой и сложный многоугольник:

Простой многоугольник – Простой многоугольник имеет только одну границу. Стороны простого многоугольника не пересекаются.

Сложный многоугольник – Сложный многоугольник – это многоугольник, стороны которого пересекаются один или несколько раз.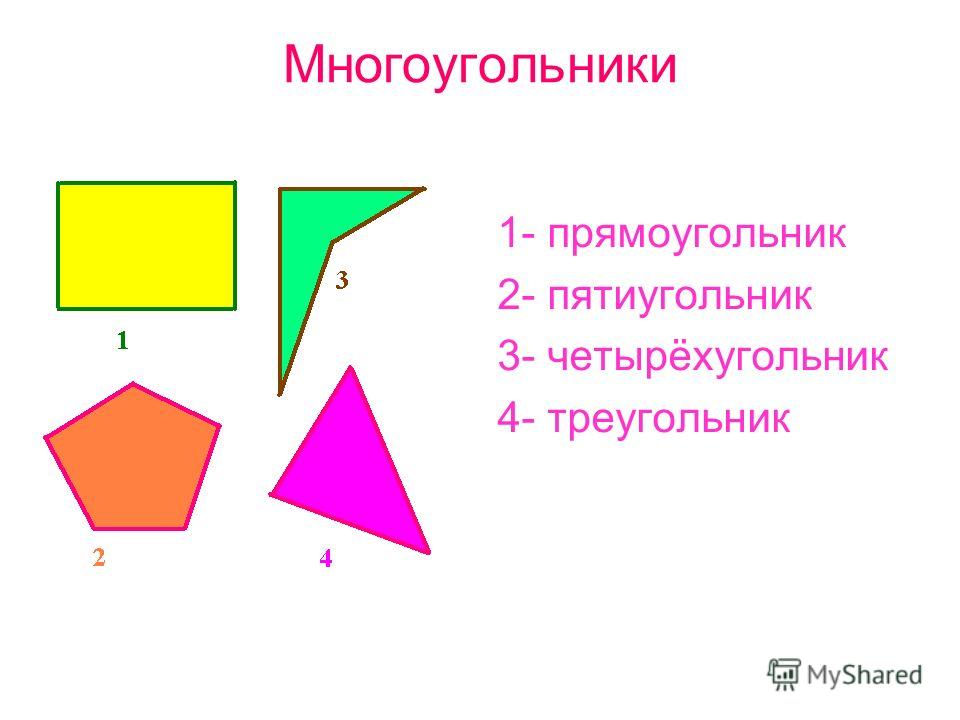

Сумма углов многоугольника

1. Сумма внутренних углов многоугольника:

Сумма внутренних углов многоугольника с n сторонами = (n – 2) × 180°

Для Пример: Рассмотрим следующий многоугольник с 6 сторонами

Здесь ∠ a + ∠ b + ∠ c + ∠ d + ∠ e + ∠ = 6 × ° = 720°       (n = 6, так как данный многоугольник имеет 6 сторон)

2. Сумма внешних углов многоугольников

Сумма внешних углов многоугольников = 360°

Сумма всегда будет равна 360 градусам, независимо от количества сторон.

Например: рассмотрим следующий многоугольник с 5 сторонами

здесь, тий M + тий N + ♂ O + тий P + ♂ Q = 360 ° 9005

ANGLES в RATGET POLYGON Q = 360 °

ANGLE

В правильном многоугольнике все его

• стороны равны
• внутренние углы равны
• внешние углы равны

Внутренний угол: 

Сумма внутренних углов многоугольника с n сторонами = (n – 2) × 180°

Таким образом, каждый внутренний угол =  (n – 2) × 180n

Внешний угол:

Сумма внешних углов многоугольников = 360°

Итак, каждый внешний угол = 360°n или неправильной, в каждой вершине многоугольника сумма внутреннего и внешнего углов равна 180°.

Решенные примеры на многоугольнике

Пример 1: Заполните пропуск.

1. Имя трехстороннего правильного многоугольника ________________.
2. Правильный многоугольник — это многоугольник, у которого все _____________ равны и все углы равны.
3. Сумма внешних углов многоугольника равна __________.
4. Многоугольник — это простая замкнутая фигура, образованная только _______________.

Решение:

1. равносторонний треугольник
2. сторон
3. 360°
4. отрезков

Пример 2: Напишите количество сторон данного многоугольника.

1. Nonagon
2. Triangle
3. Pentagon
4. Decagon

Solution:

1. 9
2. 3
3. 5
4. 10

Example 3:  Find мера каждого внешнего угла правильного многоугольника с 20 сторонами.

Решение:

Многоугольник имеет 20 сторон. Итак, n = 20.

Сумма внешних углов многоугольников = 360°

Итак, каждый внешний угол = 360°n = 360°20 = 18°

Пример 4: Сумма внутренних углов многоугольника многоугольник 1620°. Сколько у него сторон?

Решение:

Сумма внутренних углов многоугольника с n сторонами = (n – 2) × 180°

1620° = (n – 2) × 180°

n – 2 = 0920180005

n – 2 = 9

n = 9 + 2

n = 11

Итак, данный многоугольник имеет 11 сторон.

Практические задачи

360°

540°

720°

900°

Правильный ответ: 900°
У семиугольника 7 сторон. Итак, n = 7, Сумма углов многоугольника = (n – 2) × 180° = (7 – 2) × 180° = 5 × 180° = 900°

180°

360°

540 °

720°

Правильный ответ: 360°
Сумма внешних углов многоугольника всегда будет равна 360 градусам, независимо от количества его сторон.

Правильный многоугольник

Вогнутый многоугольник

Выпуклый многоугольник

Правильный ответ: Вогнутый многоугольник
Четырехугольник имеет 4 стороны. Итак, n = 4 Сумма углов многоугольника = (n – 2) × 180° = (4 – 2) × 180° = 2 × 180° = 360° 55° + 55° + 55° + четвертый угол = 360° Мера четвертого угла = 360° — 165° = 195° Таким образом, данный четырехугольник является вогнутым многоугольником, так как имеет хотя бы один внутренний угол больше 180°.

Квадрат

Равносторонний треугольник

Ромб

Шестиугольник с равными сторонами

Правильный ответ: Ромб
Какой из следующих многоугольников не является правильным?

F Часто задаваемые вопросы

Что такое диагональ многоугольника?

Диагональ многоугольника — это отрезок, соединяющий две непоследовательные вершины (углы).

Каковы свойства правильных многоугольников?

Правильный многоугольник имеет все стороны одинаковой длины и все углы равны.

Является ли круг многоугольником?

Многоугольник представляет собой замкнутую форму, состоящую из прямолинейных сегментов. Круг — это замкнутая фигура, но она состоит из кривой. Итак, круг не является многоугольником.

Какое минимальное количество сторон должно быть у многоугольника?

Многоугольник должен иметь как минимум три стороны.

Может ли количество углов и количество сторон у многоугольника быть разными?

Нет, многоугольники имеют одинаковое количество сторон и углов, потому что это замкнутые фигуры с непересекающимися линиями.

Что такое многоугольник? | TheSchoolRun

Можете ли вы отличить шестиугольники от семиугольников? Ваши восьмиугольники из ваших десятиугольников? Мы объясняем, как учат многоугольникам в начальной школе, с примерами правильных и неправильных вариантов каждой многогранной формы.

или Зарегистрируйтесь, чтобы добавить к своим сохраненным ресурсам

Что такое многоугольник?

Многоугольник — это плоская двумерная (2D) фигура с прямыми сторонами, которая полностью замкнута (все стороны соединены).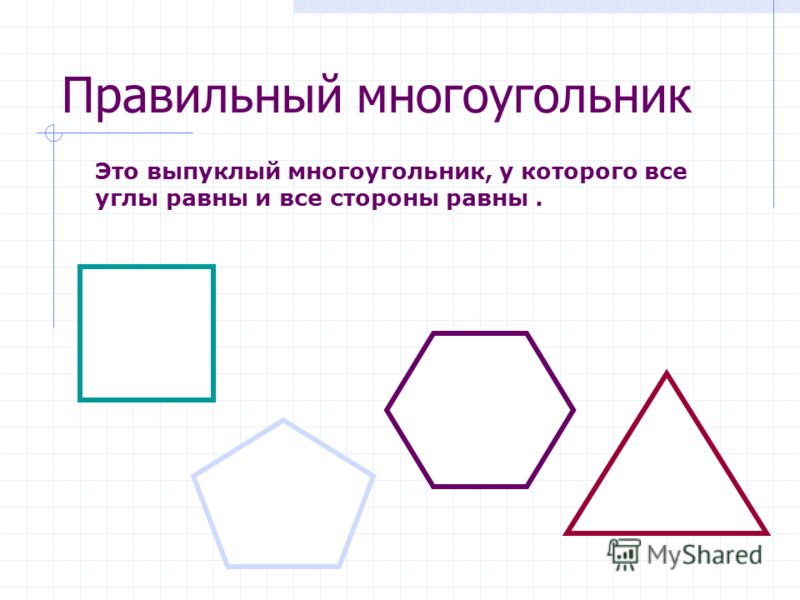 Боковые стороны должны быть прямыми. Многоугольники могут иметь любое количество сторон.
 

Многоугольник	Многоугольник не является фигурой с изогнутыми сторонами.	Форма, которая не полностью замкнута, не является многоугольником.

Правильные и неправильные многоугольники

Правильный многоугольник — это многоугольник, у которого все стороны имеют одинаковую длину и под одинаковыми углами .

Ан неправильный многоугольник — это многоугольник с сторонами и/или углами различной длины и размеров . (Although they still must be straight and joined up.)

Primary-school polygons

Polygons taught in primary school include:
 

	Regular	Irregular
Треугольник (3 стороны)
Quadrilateral (4 sides)
Pentagon (5 sides)
Шестигранник (6 сторон)
Шестигранник 91 777 0372
Octagon  (8 sides)
Nonagon  (9 sides)
Decagon (10 сторон)

*Правильный четырехугольник имеет специальное название.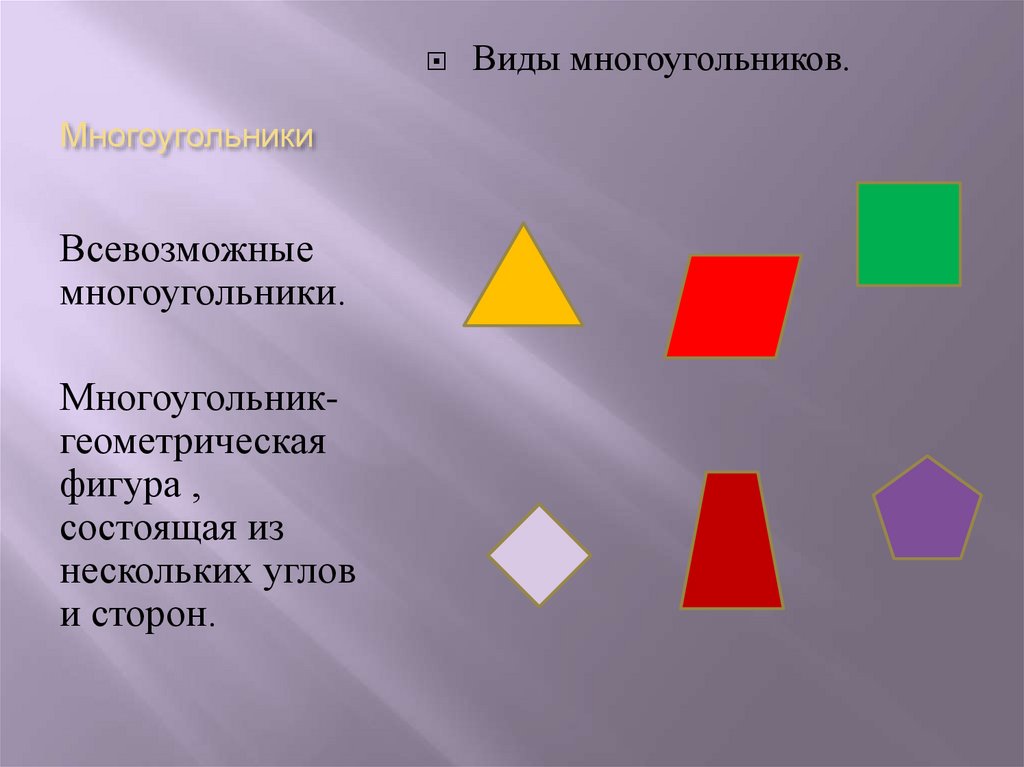 Называется квадрат.

*Треугольники бывают разных типов: 9Равносторонний треугольник 0007 является правильным треугольником , а прямоугольный треугольник и равнобедренный треугольник являются примерами неправильных треугольников.

When and how polygons are taught in primary school

	What is taught	How it might be taught
Year 1	Children are taught to name common 2D формы, включая многоугольники, такие как квадраты, прямоугольники, треугольники, пятиугольники, шестиугольники и восьмиугольники.	Дети могут выучить фигуры, выполняя упражнения на сопоставление, прогулку по фигуре на территории школы, карточки и игры. Они будут смотреть на реальные примеры форм, а также фотографии.
2-й класс	Детей научат определять свойства фигур, такие как количество сторон и вершин (углов).	Дети будут считать количество сторон и углов фигуры. Они будут описывать фигуры с помощью свойств, например: У этой фигуры 3 угла и 3 стороны. Какова форма?
3-й класс	Дети расширят свои знания о многоугольниках, включив в них различные типы треугольников и четырехугольников. Они познакомятся с семиугольниками, девятиугольниками и девятиугольниками. Знание свойств формы будет включать углы и симметрию этих многоугольников.	Дети будут описывать формы и определять их, используя их свойства, включая симметрию и углы. Их могут попросить отсортировать фигуры в соответствии с их свойствами, используя диаграммы Венна и диаграммы Кэрролла.
4-й класс	Детей учат сравнивать длины и углы многоугольников, чтобы определить, правильные они или неправильные. Будут использоваться слова «многоугольник», «правильный» и «неправильный».	Детям будет дан набор многоугольников, которые нужно отсортировать на правильные и неправильные; это может быть выполнение практических заданий или использование ИКТ. Share : Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт