На окна решетки образцы: Решетки на окна — 100 фото готовых решений. Лучшие варианты для частного дома
Решетки на окна — 100 фото готовых решений. Лучшие варианты для частного дома
В зимний период времени многие частные загородные владения остаются нежилыми, поэтому, подобные дома становятся простой добычей для злоумышленников. Чтобы избавить себя от ненужных переживаний и обеспечить своему жилью полную безопасность, хозяева загородных домов устанавливают на их окна решётки.
Однако выбор такого варианта безопасности вовсе не простой, так как современный рынок предлагает разнообразие оконных конструкций, в котором несложно потеряться, ведь решётки отличаются по форме, виду, а также назначению. Поговорим, как правильно приобрести решётки на дачные оконные проёмы, чтобы быть полностью уверенным в их безопасности.
Краткое содержимое статьи:
Классификация
Ориентируясь на базовые виды, можно выделить такие конструкции, как кованые, а также сварного типа.
К более востребованным элементам относятся сварные конструкции по причине доступности ценовой категории, практичности и лёгкости.
Изделия из ковки не такие востребованные по причине дороговизны. Но этот минус имеет вполне обоснованные объяснения, так как кружево из ковки, созданное по персональному заказу, впишется в любой дизайн, при этом удовлетворит все пожелания будущего хозяина.
Существует и иная разновидность решёток для дачных окон в зависимости от нюансов их установки, по этой причине если нужно купить подобные конструкции недорого, следует сделать грамотный выбор. Создаются данные конструкции из профилей металлических, которые имеют разную форму, длину, изготовителей.
Так, выбором во многом зависит от внешних характеристик и формы необходимых решёток. При правильном выборе можно изготовить эксклюзивные защитные оконные решётки и получить множество великолепных идей для обустройства необычного экстерьера.
Подходящие дачные решётки
По особенностям и варианту установки оконные элементы бывают нескольких типов.
Съёмные модели являются цельным вариантом. В критичных случаях подобную конструкцию можно убрать с окна, однако благодаря плотному закручиванию элементов, провести подобные манипуляции крайне сложно. Вероятность устранения не лучшим образом отражается на прочности изделия в дальнейшей эксплуатации.
Варианты стационарного типа можно крепить к фасаду наглухо. Подобного вида защита относится к одной из самых долговечных. Данного плана модели вскрыть практически невозможно, так как они имеют внушительную толщину, а также соответствуют требуемым нормам пожаробезопасности.
Недостаток состоит в том, что в критическом случае у хозяев не будет возможности выбраться на улицу из дома через оконный проём, поэтому лучше комбинировать подобные изделия с различными другими вариантами решёток.
Решётки распашного вида имеют одну, либо пару створок, которые при необходимости несложно устраняются. Установка изделий проводится с использованием высокопрочного крепления, которое уходит достаточно глубоко непосредственно внутрь настенной поверхности. Створка закрывается на специальную щеколду.
Установка изделий проводится с использованием высокопрочного крепления, которое уходит достаточно глубоко непосредственно внутрь настенной поверхности. Створка закрывается на специальную щеколду.
Если в процессе изготовления использованы мизерные прутья, то открыть подобные элементы невозможно. В данном варианте прутья перерезаются специальным инструментом для работы по металлу.
Оконные решётки раздвижные представляют собой самые удобные в эксплуатации модели. Их закрывание и открывание осуществляется достаточно просто, а необычное размещение прутьев даёт им возможность складываться по типу гармошки. Данного вида элементы надёжно защищают оконные проёмы, а также двери.
Один минус — простота оформления и невозможность создания привлекательного узора. К тому же, надёжность защиты, которую обеспечивает подобная конструкция, средняя, так как для бесперебойности функционирования механизма применяются прутья-пластины, поддающиеся беспроблемной поломке.
Виды решёток раздвижного типа
Одностворчатые. В таких конструкциях одна сторона крепится к несущей стойке, а другая — к контактной. Подобного вида вариация позволяет элементам открываться в разные стороны — неоспоримый плюс.
Двустворчатые варианты представлены в виде нескольких подвижных композиций, запирающиеся в центральной части оконного проёма, незначительно смещающиеся в одну сторону.
Композиции вертикальные оснащены створками, а также соединением крестообразного типа.
Все перечисленные оконные решётки, фото которых представлены в каталоге, создаются требуемого размера. Таким образом, данные изделия могут иметь несколько видов, однако чтобы они были полезны в использовании, следует сочетать типовые конструкции с решёткой съёмной, либо распашного типа.
Если вы желаете преобразить окна своего жилья и купить для них решётки по доступной стоимости, тогда оптимальным решением может стать приобретение кованых элементов съёмного вида.
Благодаря размеру полотна можно создать эксклюзивный и привлекательный рисунок.
Особенности приобретения решёток
Как правило, изготовлением подобных конструкций занимаются специализированные фирмы, поэтому предпочтительно остановить выбор непосредственно на изделиях, которые предлагают именно они. В основном, данные компании предлагают разнообразие качественных моделей решёток для оконных дачных проёмов.
Некоторые элементы решёток из ковки являются истинным произведением искусства и производятся исключительно одарёнными мастерами. В подобных случаях необязательно обращаться в огромные фирмы, так как можно сотрудничать и с маленькой мастерской для получения прекрасного результата.
Немаловажный показатель безупречного качества создаваемых конструкций — возраст фирмы, которые изготавливают их. Всё же элементы считаются не настолько востребованными и отличаются минимальным спросом среди населения.
При необходимости установки оконных решёток сварных или другого вида, ориентируйтесь не на рекламу, а только на положительные отзывы.
Решётки своими руками: делаем грамотный выбор
Стационарные
Подобные модели отлично справляются с функцией охраны. Однако необходимо смириться с их внешней простотой и другими нюансами в виде невозможности комбинирования и невозможности снятия.
Достоинства
- Отличная защита от нежелательного проникновения в дом;
- Несложность процесса установки;
- Простота производственного процесса;
- Высокая степень надёжности в отношении безопасности.
Минусы
- Недостаточная огнеупорность;
- Внешняя простота.
Установка
Данные конструкции просты в монтаже, но при условии, если вы будете придерживаться соответствующей инструкции. При отсутствии усидчивости и свободного времени альтернативным выходом станет приобретение решёток, так как сегодняшний рынок готов предложить множество элементов из самых разнообразных современных материалов, которые привнесут в ваше жильё эстетику.
Раздвижные
Это достойный вариант для тех, кто является приверженцем эстетики, элегантной простоты. Этого типа модели отличаются рядом особенностей.
Плюсы
- Универсальность использования и удачная сочетаемость с каждым фасадом;
- Простота эксплуатации;
- Внешняя привлекательность;
- Требует минимум места;
- Многообразие модельного ряда.
Монтаж
Существует несколько главных способов установки таких конструкций — выкладка с внутренней части оконного проёма и внешняя. Первый метод достаточно удобен и весьма надёжен, так как благодаря креплению изнутри систему использовать очень просто.
Решётки, монтаж которых осуществлён изнутри, характеризуются высокой степенью безопасности в отношении нежелательного проникновения в дом, по этой причине при выборе подходящих конструкций следует уделить максимум внимания удобству в процессе эксплуатации.
Съёмные модели
Механизм элементов представлен в виде шпилек с резьбой.
Плюсы:
- Возможность устранения элементов;
- Недорогая ценовая категория;
- Простота проведения монтажных работ;
- Внешняя привлекательность.
Минусы: Возможность устранения для злоумышленников.
Установочный процесс
Если вы решили поставить на оконные проёмы схемного вида решётки, тогда придётся хорошо поработать, чтобы создать надёжную и красивую конструкцию. Правильный выбор в сторону конкретного вида решёток, их монтаж даст возможность владельцам строения полную безопасность, а также огромное эстетическое удовлетворение.
Фото решеток на окна
youtube.com/embed/j7B3YBVstSw?rel=0&controls=0&showinfo=0″ frameborder=»0″ allowfullscreen=»allowfullscreen»>Пост опубликован: 02.12
Присоединяйтесь к обсуждению:
detector
Решетки на окна — 89 фото лучших примеров безопасно окна 2019 годаall-designstroy.ru
Зачастую решетки на окна ставят жители частных домов, коттеджей и жители первых этажей многоквартирных домов. Это не удивительно, ведь люди хотят обезопасить себя и близких от возможных проблем.
В основном решетки ставят с первого по третий этаж, потому что забраться на первые этажи не сложно.
Установив качественные решетки на окна можно не беспокоится о своей безопасности. Также решетки не только оберегают имущество от кражи, но и эффектно смотрятся.
Какие бывают оконные решетки?
Решетка для окна может быть любой формы и выполнена по личному заказу. Каждый сможет выбрать для себя подходящий вариант, который украсит фасад здания и обезопасит от незваных гостей.
Металлические
Такие решетки выполнены из металлов повышенной прочности, могут быть сварными или кованными. Бюджетным вариантом является простая решетка.
Кованые изделия стоят значительно дороже, за счет трудоемкости изготовления.
Сварные
Данные решетки выполняют из металлических прямых прутов, которые могут иметь разное сечение.
Красотой такие изделия не отличаются, за то первостепенные функции выполняют на отлично. Все швы в ходе производства фиксируются сваркой.
Кованые
Стоит отметить тот факт, что при изготовлении кованых решеток зачастую используется закаленный метал с повышенной прочностью.
Такой материал не имеет проблем с коррозией и является наиболее прочным металлическим изделием. Из кованых элементов возможно создание неповторимых решеток для окон.
Из кованых элементов возможно создание неповторимых решеток для окон.
Декоративные деревянные
Решетки для окон могут быть самыми разными и функции таких изделий направлены не только на защиту имущества, но а также придать фасаду особый стиль.
Виды оконных решеток
Раздвижные
Складываются решетки по типу гармошки, прячась в специальный отсек. Они просты и надежны в эксплуатации, но прочность значительно ниже, чем у других.
Конструкция решеток позволяет выбрать оптимальный вариант сборки, в одну сторону либо в обе стороны. Замок для решетки может быть встроенным либо навесным.
Распашные
Такие оконные решетки наиболее популярны, удобны в эксплуатации и имеют хорошие показатели прочности.
При выборе такой решетки следует учесть тот факт, что при минусовых температурах работоспособность данной системы выходит из под контроля.
Рольставни
Рольставни в настоящий момент применяются для оконных и для дверных проемов. Они широко используются в служебных и торговых помещениях.
Они широко используются в служебных и торговых помещениях.
Такие изделия отлично зарекомендовали себя, как в надежности от взлома, так и в защите от солнечного света и шума. Также являются незаметными в сложенном виде. Эксплуатационные характеристики высокие.
Достоинства оконных решеток неоспоримы, их наличие на первых этажах многоэтажных и частных домов обоснованны.
Решетки для окон можно установить без привлечения специалистов, при определенных навыках.
Креплениями могут быть:
- Металлические элементы — данные элементы используются для сварных решеток. Главное при выборе данного способа это наличие крепких, прочных стен.
- Метизы — метизами крепят кованые решетки.
- Шпильки — этот вид креплений используется для установки решеток в деревянных домах.
Каждый тип креплений относится к разным видам оконных решеток, необходимо помнить об этом. Наличие оконных решеток способно обезопасить себя и своих близких.
Фото решеток на окна
Также рекомендуем просмотреть:
- Наличники на окна
- Регулировка пластикового окна
- Рольставни на окна
- Мансардные окна
- Как поставить окна на лоджию
- Устанавливаем балконные рамы
- Отделка откосов
- Запотевание пластиковых окон
- Арочные окна
- Установка пластиковых откосов на окна
- Установка деревянного подоконника
Эскизы металлических решеток на окна.
 Эскизы металлических решеток на окна.
Эскизы металлических решеток на окна.Решетки
Решетка кованая РК-168
Решетки кованые РК-207
Решетка на окно РС-88
Решетка РС-15 (рис. Монастырка)
Решетки сварные РС-27
Решетка на окно РС-89
Решетки кованые РК-105
Решетки кованые РК-10
Решетки сварные РС-134
Решетки сварные РС-23
Решетки кованые РК-199
Стеллаж лофт СЛ-2
Стеллаж лофт СЛ-1
Ворота откатные, усиленые, промышленного назначения
Решётки кованые РК-196
Кованые решетки на заказ, любого дизайна и сложности, изготовление в сжатые сроки
Навес с монолитным поликарбонатом НП-80
Решётки кованые РК-112
Цветники на окна КЦ-31
Решетки кованые РК-109
Цветники на окна КЦ-30
Решетки кованые РК-106
Решетки кованые РК-105
Решётки кованые РК-103
Кованый забор КЗ-8
Решётки кованые РК-101
Решетки кованые РК-19
Решетки кованые РК-9
Решетка антикошка РА-14
Решетки сварные РС-24
Внутренние кованые решетки ВР-7
Внутренние кованые решётки ВР-5
Решетки сварные РС-17
Решетки кованые РК-1
Решетки сварные РС-4
Решетки сварные РС-16
Решетка на окно РС-95
Решетка на окно РС-82
Решетка на окно РС-71
Решетки сварные РС-11
Решетки сварные РС-5
Откатные кованые ворота КВ-13
Дверь решетчатая ДР-1
Раздвижные решетки на двери РР-5
Кованые навершия над забором
Решетки кованые РК-9
Цветник кованый КЦ-07
Цветник кованый КЦ-02
Решетки кованые РК-14
Решетки кованые РК-13
Французский балкон ФБ-7
Французский балкон ФБ-6
Решетки сварные РС-36
Решетки кованые РК-17
Дутые решетки Д-19
Решетки кованые РК-23
Решетки кованые РК-25
Решетки распашные РС-45
Решетки сварные РС-44
Решетки сварные РС-38
Французский балкон ФБ-1
решетка распашная РР-16
Перила кованые в ландшафте ПК-83
Забор ЗД-19
Решетки кованые РК-35
Кованый цветник КЦ-21
Решетка кованая РК-102
Решетки сварные РС-45
Решетки сварные РС-46
Решетка кованая РК-122
Решетки кованые РК-78-1
Решетки кованые РК-159
Решетки кованые РК-157
Решетка на окно РС-83
Цветник кованый КЦ-15
Решетки кованые РК-54
Решетки кованые РК-55
Решетки кованые РК-56
Дутая решетка д-3
Решетки кованые РК-64
Решетка сварная РС-58
Дутая решетка д-16
Решетки кованые РК-66
Решетки кованые РК-69
Решетки кованые РК-70
Накладные решетки на дачу РС-103
Решетки на балкон РБ-39
Кованая решетка КР-18-3
Решетка антикошка РА-2
Дутая решетка Д-7
Решетки кованые РК-74
Решетка кованая РК-15-6
Решетка кованая РК-12
Решетки на балкон РБ-75 остеклёный
Решетки кованые РК-77
Решетка на окно РС-81 (рис. Волна)
Волна)
Цветник кованый КЦ-04
Решетка на окно РС-77
дутая решетка д-1
Решетки кованые РК-96
Решетка сварная РС-62
Решетки на окна РС-60
Решетка сварная РС-63
Решетки кованые РК-85
Решетка кованая рк-17
Решетка на окно РС-79
Решетка на окно РС-150
Решетка сварная РС-54
Решетки на балкон
Дутая решетка д-2
Цветник кованый КЦ-08
Решетка кованая РК-211
Решетка на окно РС-102
Решетка кованая РК-114
Решетки кованые РК-7
Распашные кованые решётки РК-5
Решетка кованая РК-107
Дутая решетка Д-18
Решетка кованая РК-155
Решетка кованая РК-50
Решетка кованая РК-20-3
Кованая решетка РК-55
кованые решетки РК-101
Решетка на окно РС-74
Решетка на окно РС-78
Кованые решетки РК-20-6
Решетки кованые РК-17
Кованая решетка КР-18-2
Кованые решетки РК-38
Решетка кованая РК-19
Решетка кованая РК-18
Кованая решетка с лепестками РК-20-5
Кованая решетка с пиками РК-20-4
Решетка кованая дутая РКД-1
Сварные решетки РС-64
Решетка сварная РС-68
Решетка сварная РС-66
Решетка сварная РС-65
Решетки на окна РС-59
Решетки на окна РС-61
Решетка на окно РС-99
Дутая решетка Д-9
Решетка на окно РС-131
Решетки сварные РС-70
Решетка на окно РС-101
Решетки сварные РС-69
Навесы
Навес с мягкой кровлей НП-72
Навес над входом металлический НП-32
Навес с монолитным поликарбонатом сложной формы НП-74
Навес с поликарбонатом НП-73
Навес с сотовым поликарбонатом НП-70
Навес с поликарбонатом НП-55
Навес над входом в подвал НП-52
Навес с поликарбонатом НП-51
Радиусный навес с поликарбонатом НП-49
Навес с поликарбонатом НП-47
Навес с металлочерепицей
Навес с поликарбонатом НП-39
Навес кованый с поликарбонатом НП-37
Навес на дачу НП-35
Навес над крыльцом НП-34
Навес над терминалом НП-31
Навес с поликарбонатом НП-30
Навес с поликарбонатом НП-29
Навес с поликарбонатом НП-28
Навес из поликарбоната НП-23
Навес из поликарбоната НП-21
Навес из поликарбоната НП-13
Навес для дачи НП-17
Металлическая лестница под крыльцо МЛ-1
Навес из поликарбоната НП-15
Навес с металлочерепицей НП-7
Навес с влагостойкой фанерой под мягкую кровлю НП-10
Навес с поликарбонатом НП-9
Навес с поликарбонатом НП-11
Козырьки
Козырёк над входом КК-65
Кованый козырёк с мягкой кровлей КК-63
Козырек над входом КК-61
Козырек над входом КК-60
Козырек над входом КК-57
Козырек над входом КК-58
Козырек над входом КК-56
Козырек над входом в подвал КК-55
Козырек на балкон КК-53
Кованый козырёк над приямком КК-51
Кованый козырёк КК-48
Кованый козырек с поликарбонатом КК-47
Кованый козырёк над входом КК-46
Кованый козырёк над входом КК-45
Кованый козырёк КК-44
Кованый козырек КК-42
Козырек над входом КК-35
Козырек над стеклянным тамбуром КК-33
Козырек над входом КК-30
Козырек над входом КК-31
Кованый козырёк КК-28
Кованый козырек КК-21
Кованый козырек КК-19
Кованый козырек КК-15
Входная группа КВГ-1
Кованый козырек К-9
Кованый козырек КК-14
Кованый козырек КК-12
Кованый козырек КК-13
Перила
Перила кованые ПК-239
Перила кованые ПК-236
Перила кованые ПК-235
Перила кованые ПК-232
Перила кованые ПК-230
Перила сварные ПК-229
Перила сварные ПК-227
Перила на винтовую лестницу ПК-226
Кованое ограждение ПК-225
Кованые ограждения ПК-224
Кованые ограждения ПК-223
Перила кованые ПК-222
Перила на лестницу ПК-221
Перила на лестницу ПК-220
Перила кованые ПК-219
Перила на лестницу ПК-218
Перила на лестницу ПК-217
Кованые перила ПК-215
Кованые перила ПК-214
Кованые перила ПК-213
Кованые перила ПК-212
Кованые перила ПК-211
Кованые перила ПК-210
Кованые перила ПК-209
Кованые перила ПК-208
Кованые перила ПК-207
Кованые перила ПК-206
Кованые перила ПК-205
Кованые перила ПК-204
Перила кованые ПК-203
Перила кованые ПК-202
Перила кованые ПК-201
Перила кованые ПК-198
Перила кованые ПК-194
Перила кованые ПК-193
Перила кованые ПК-190
Перила кованые ПК-189
Перила кованые ПК-188
Перила кованые ПК-187
Лестничные перила ПК-149
Лестничные перила ПК-148
Лестничные перила ПК-147
Перила кованые ПК-52
Лестничные перила ПК-146
Лестничные перила ПК-144
Перила для лестниц ПК-141
Уличные ограждения для крыльца ПК-137
Лестничные ограждения ПК-136
Лестничные ограждения ПК-135
Лестничные ограждения ПК-134
Перила кованые на лестницу ПК-86
Лестничные ограждения ПК-127
Перила для лестниц ПК-101
Перила кованые ПК-124
Перила уличные ПК-114
Перила кованые ПК-113
Перила кованые ПК-112
Французский балкон ФБ-5
Защитные ограждения для французских окон ПК-95
Лестничные ограждения ПК-92
Ограждения для лестниц с деревянными ступенями ПК-94
Перила на лестницу забежные ПК-91
Перила кованые ПК-89
Перила кованые на лестницу ПК-85
Кованый козырёк над входом КК-40
Перила кованые на парадную лестницу ПК-84
Перила кованые на лестницу ПК-84
Кованые перила на лестницу ПК-17
Перила кованые на лестницу ПК-80
Перила кованые для лестниц ПК-80
Перила кованые ПК-77
Перила кованые ПК-76
Перила кованые ПК-71
Перила для лестниц ПК-73
Перила для лестниц ПК-72
Перила кованые ПК-66
Перила кованые ПК-65
Перила кованые ПК-62
Перила кованые ПК-58
Кованые перила ПК-18
Кованые перила ПК-15
Кованые перила ПК-17
Кованые перила ПК-14
Перила кованые ПК-55
Кованые перила ПК-16
Перила кованые ПК-54
Перила кованые ПК-48
Кованые перила ПК-22
Кованые перила ПК-25
Кованые перила ПК-19
Кованые перила ПК-20
Кованые перила ПК-5
Перила кованые ПК-46
Перила кованые ПК-45
перила ПК-43
перила для лестниц ПК-41
Перила для балконов ПК-44
Кованые перила ПК-26
Ставни жалюзи СЖ-3
Мы перезвоним и ответим на все Ваши вопросы
Отправить
Решётки на окна – эскизы
Главная » Окна » Решётки на окна – эскизы
Самым уязвимым местом в доме, с точки зрения несанкционированного проникновения, были и остаются окна. Нижние этажи многоэтажных домов и частные жилые постройки как только не предохраняются от квартирных воров. Но какие бы современные сигнализации и средства охраны мы ни устанавливали бы, ничего так эффективно не препятствует взлому, как решетки на окна.
Нижние этажи многоэтажных домов и частные жилые постройки как только не предохраняются от квартирных воров. Но какие бы современные сигнализации и средства охраны мы ни устанавливали бы, ничего так эффективно не препятствует взлому, как решетки на окна.
Содержание:
- Применение металлических решеток
- Способы монтажа оконных решеток
- Как правильно выбрать решетку
- Материалы и способы изготовления
Применение металлических решеток
Видов оконных решеток и вариантов исполнения есть немыслимое количество, но наиболее распространены сварные или кованые решетки на окна эскизы которых мы будем рассматривать сегодня. По форме различают также решетки луковицы, арочные и прямые решетки. Наиболее ценными с точки зрения эстетики всегда были кованые конструкции, но они же и самые дорогие.
В первую очередь, решетки на окнах обеспечивают безопасность квартиры или дома. Хотя о стопроцентной гарантии неприступности жилья говорить не приходится, решетка значительно усложнит путь к семейным сокровищам квартирного вора. Другая и, пожалуй, не менее важная составляющая, которая влияет на выбор охранных конструкций — эстетическое исполнение. Никто не захочет жить за не слишком эстетичной казенной решеткой, пусть она будет хоть сто раз крепкой.
Другая и, пожалуй, не менее важная составляющая, которая влияет на выбор охранных конструкций — эстетическое исполнение. Никто не захочет жить за не слишком эстетичной казенной решеткой, пусть она будет хоть сто раз крепкой.
Способы монтажа оконных решеток
Чаще всего решетки устанавливают вместе с заменой оконных блоков. Это наиболее простой путь и наиболее эффективный, поскольку так закрепить каркас решетки, как это можно сделать при снятом оконном блоке, не получится никогда. Тем не менее, если же окна демонтировать неохота, существуют несколько методов крепления оконных решеток в проем.
Первый — самый эффективный, но сложный. Для этого необходимо связать силовую структуру окна с решеткой. Поскольку сварка здесь не пройдет, то нужно обеспечивать доступ для резьбового или крюкового соединения. А это довольно долго и сложно. Долго, потому что приходится разрушать часть оконного проема, а после монтажа оконной решетки снова его восстанавливать.
Второй способ более простой, но менее надежный. Решетка может быть установлена на анкера, которые внедрены в стену или в оконный проем. Так проще и быстрее установить любую металлическую решетку. Для этого в стену всверливается определенное количество анкеров, к которым после приваривается каркас решетки.
Решетка может быть установлена на анкера, которые внедрены в стену или в оконный проем. Так проще и быстрее установить любую металлическую решетку. Для этого в стену всверливается определенное количество анкеров, к которым после приваривается каркас решетки.
Как правильно выбрать решетку
Решетки также могут иметь разные методы фиксации. При условии, что каркас решетки установлен одним из тез способов, о котором мы говорили, сама решетка может быть как несъемной, стационарной, так и съемной. Есть конструкции решеток с возможностью открывания створок, с местом для кондиционера. Также существуют раздвижные и распашные решетки. Какую из них выбрать?
Довольно неоднозначные напрашиваются ответы, поскольку плюсы и минусы есть у каждой из конструкций и здесь стоит учитывать некоторые нюансы:
- Если спросить у пожарного инспектора, какие типы решеток посоветовал бы он, то его выбор, скорее всего, пал бы на любые решетки, кроме стационарных, закрепленных наглухо.
 И он будет совершенно прав. При непредвиденных обстоятельствах с такой решеткой не получится воспользоваться окном, как запасным выходом.
И он будет совершенно прав. При непредвиденных обстоятельствах с такой решеткой не получится воспользоваться окном, как запасным выходом. - Распашные и раздвижные решетки — напротив. Открываются легко и просто, а закрываются при помощи замка встроенного или даже навесного. Единственное неудобство — нужно всегда иметь под руками ключ, иначе такая решетка автоматически превращается в стационарную.
- С точки зрения участкового милиционера, самым лучшим вариантом станет глухая стационарная решетка. Ее труднее всего взломать, а перерезать болгаркой без шума и пыли не получится.
- Если проконсультироваться с мудрым владельцем квартиры, то он скажет, что на всю квартиру вполне достаточно одной распашной или раздвижной решетки, а остальные окна можно делать глухими.
Материалы и способы изготовления
По материалу изготовления решетки могут выполняться из нескольких видов металлопроката: круглого прута сечением от 10 до 20 мм, квадратного прута сечением от 12 до 16 мм (по длине одной стороны), также нередко используют стальную мощную полосу шириной от 10 мм и толщиной не менее 5 мм. Наиболее убедительно выглядят комбинации из всех этих материалов.
Наиболее убедительно выглядят комбинации из всех этих материалов.
По типу фиксации элементов решетки между собой, решетки могут быть сварными или коваными. Сварные конструкции применяются чаще всего, как утилитарные с минимумом декоративных элементов, но с максимальной степенью защиты. Полностью кованые конструкции — изящны, эстетичны и могут по-настоящему украсить фасад дома. Но их стоимость в несколько раз превысит цену сварной решетки. Компромиссный вариант, когда некоторые кованые декоративные элементы привариваются к сварной решетке — самый оптимальный по цене, а по виду может и не отличаться от кованых конструкций.
Таким образом, выбрав решетку на окна, можно обезопасить дом от квартирных воров и сделать фасад еще чуточку интереснее.
Читайте также Решетки на окна своими руками
Решётки на окна по цене от производителя
Сварная решетка на окна №157
от 940 руб/м2
+
Купить в 1 клик
Металлическая решетка на окно №31
от 950 руб/м2
+
Купить в 1 клик
Глухая решетка на окно №22
от 980 руб/м2
+
Купить в 1 клик
Сварная решетка на окна №20
от 950 руб/м2
+
Купить в 1 клик
Сварная решетка на окна №11
от 980 руб/м2
+
Купить в 1 клик
Решетка на балкон №11
от 1190 руб/м2
+
Купить в 1 клик
Сварная распашная открывающееся решетка №166
от 1320 руб/м2
Скидка: 12%
Старая цена:
1500 руб/м2
+
Купить в 1 клик
Кованая решетка на окно №93
от 2610 руб/м2
+
Купить в 1 клик
Решетка на окно из металла №92
от 2600 руб/м2
+
Купить в 1 клик
Кованая решетка с цветочницей на окно №83
от 2790 руб/м2
+
Купить в 1 клик
Кованая решетка на окно №74
от 2690 руб/м2
+
Купить в 1 клик
Решетка для ребенка №58
от 2680 руб/м2
+
Купить в 1 клик
Кованая решетка на окно №56
от 2600 руб/м2
+
Купить в 1 клик
Кованая решетка на окно №55
от 2750 руб/м2
Скидка: 15%
Старая цена:
3240 руб/м2
+
Купить в 1 клик
Кованая решетка на окно №51
от 2620 руб/м2
Скидка: 15%
Старая цена:
3090 руб/м2
+
Купить в 1 клик
Кованая защитная решетка на окно №39
от 2870 руб/м2
Скидка: 15%
Старая цена:
3380 руб/м2
+
Купить в 1 клик
Кованая решетка с цветником на окно №18
от 2800 руб/м2
+
Купить в 1 клик
Кованая решетка от выпадения детей на окно №6
от 2850 руб/м2
+
Купить в 1 клик
Решетка на окно квартиры №4
от 2760 руб/м2
Скидка: 12%
Старая цена:
3140 руб/м2
+
Купить в 1 клик
Сварная решетка на окна №151
от 960 руб/м2
+
Купить в 1 клик
Решетка на окно из металла №149
от 960 руб/м2
+
Купить в 1 клик
Сварная высокая решетка на окна №30
от 930 руб/м2
+
Купить в 1 клик
Сварная решетка на окна №23
от 940 руб/м2
+
Купить в 1 клик
Сварная защитная решетка на окна №2
от 980 руб/м2
+
Купить в 1 клик
Решетка на лоджию или балкон №8
от 1030 руб/м2
+
Купить в 1 клик
Раздвижная решетка на окна №3
от 3500 руб/м2
Скидка: 8%
Старая цена:
3810 руб/м2
+
Купить в 1 клик
Раздвижная решетка на окна №2
от 3700 руб/м2
+
Купить в 1 клик
Решетка гармошка на окно №1
от 3400 руб/м2
Скидка: 5%
Старая цена:
3580 руб/м2
+
Купить в 1 клик
Решетка на окно металлическая внутренняя №168
от 1290 руб/м2
Скидка: 10%
Старая цена:
1440 руб/м2
+
Купить в 1 клик
Сварная распашная решетка на окна №167
от 1300 руб/м2
Скидка: 7%
Старая цена:
1400 руб/м2
+
Купить в 1 клик
Решётки на окна сварные и кованые в Москве от завода-производителя «РУСРЕШЕТКА»
Компания «РУСРЕШЕТКА» производит и продает решетки на окна из металла, заборы, ворота, ограждения, козырьки, перила и предметы декора.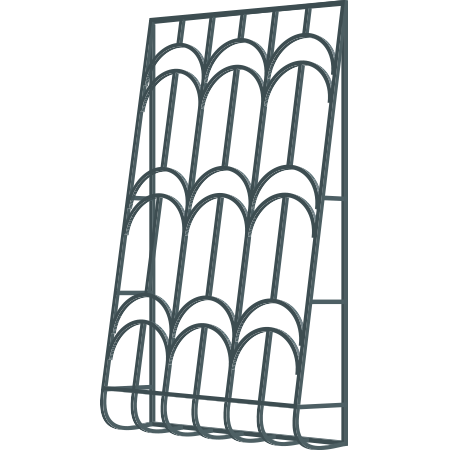 Создаем, доставляем и монтируем металлические конструкции для физических и юридических лиц в Москве и по всей Московской области.
Создаем, доставляем и монтируем металлические конструкции для физических и юридических лиц в Москве и по всей Московской области.
Чаще всего к нам обращаются за покупкой и монтажом металлических оконных решеток, которые надежно защищают оконные проемы зданий от хулиганов и воров. Их устанавливают также, чтобы дети или домашние животные не выпали из окна. Третья важная функция металлических решеток – оформление оконного проема.
Какие решетки мы производим?
В каталоге представлены кованые, распашные, сварные, дутые решетки, а также модели на кондиционер. Всего в ассортименте более 1000 различных вариантов, отличающихся стоимостью и конструкцией. В наличии как экономичные изделия, так и дорогие эксклюзивные. Мы также изготавливаем решетки по вашему эскизу или эскизу нашего дизайнера на основе ваших предпочтений и пожеланий. Это возможно благодаря собственному современному производству.
Сварные решетки
Самый популярный вид решеток, самый простой и бюджетный вариант. Представляет собой металлическую целиковую конструкцию из прутьев. Главная задача – защита от проникновения злоумышленников. Второстепенная – декор фасада сооружения. Прекрасно подходит и для помещений на первых этажах в городе, и для частных загородных домов. Сварные решетки изготавливаются быстрее всего. Обычно все готово уже через 2-3 дня.
Представляет собой металлическую целиковую конструкцию из прутьев. Главная задача – защита от проникновения злоумышленников. Второстепенная – декор фасада сооружения. Прекрасно подходит и для помещений на первых этажах в городе, и для частных загородных домов. Сварные решетки изготавливаются быстрее всего. Обычно все готово уже через 2-3 дня.
Коварные решетки
Еще один популярный вариант. Они так же как и сварные, защищают помещение от грабителей и хулиганов. Но в отличие от сварных, кованые смотрятся еще более эстетично. Их можно изготовить по нашим готовым эскизам или по вашим задумкам. Кованые изделия создаются вручную, поэтому они уникальны.
Дутые решетки
Дутые решетки – это вид решеток, имеющий объем, чаще это выпуклость, располагающуюся снизу или наверху. Делается только для эстетики, никакой практической значимости она не несет.
Распашные решетки
Главное отличие распашной решетки – это возможность ее открыть изнутри. При этом снаружи ее открыть нельзя. Обратите внимание при установке решеток, что в помещении по нормам пожарной безопасности хотя бы одна должна обязательно открываться.
Обратите внимание при установке решеток, что в помещении по нормам пожарной безопасности хотя бы одна должна обязательно открываться.
Решетки для кондиционера
Главная задача решетки для кондиционера – защита от грабителей и вандалов. Также решетка надежно защищает внешний блок от ветра, дождя, снега, льда, падающих из чужих окон предметов. Менее явная функция – скрыть некрасивый и громоздкий блок кондиционера или придать ему более эффектный и изящный вид, украсить фасад дома.
Чтобы заказать решетки на окна в Москве, напишите нам на электронную почту или позвоните по указанному в разделе «Контакты» телефону. Наш менеджер ответит на вопросы, поможет сделать выбор и примет заявку.
Изготовление решеток на окна от компании «РУСРЕШЕТКА»
Мы занимаем одну из лидирующих позиций на рынке металлоконструкций не просто так. Наш собственный производственный цех способен создавать не только типовую продукцию, но и эксклюзивные изделия. Над ними работают профессиональные дизайнеры. Они помогут воплотить идеи и пожелания в жизнь. Дизайнеры имеют опыт работы более 10 лет, они регулярно изучают тренды и совершенствуют свои умения, благодаря чему вы получаете дизайнерское решение.
Наш собственный производственный цех способен создавать не только типовую продукцию, но и эксклюзивные изделия. Над ними работают профессиональные дизайнеры. Они помогут воплотить идеи и пожелания в жизнь. Дизайнеры имеют опыт работы более 10 лет, они регулярно изучают тренды и совершенствуют свои умения, благодаря чему вы получаете дизайнерское решение.
Выезд замерщика осуществляется бесплатно. Вы можете приобрести продукцию без замера, но при этом есть риск, что решетки окажутся не по размеру. Вы потеряете время и деньги. Не пропускайте этот этап во избежание недоразумений. Чтобы вызвать замерщика бесплатно и получить расчет стоимости металлической решетки, напишите или позвоните нам.
Почему с нами выгодно и приятно сотрудничать?
- У нас собственное производство. Производственный цех оборудован современной техникой. Регулярно поставляются качественные материалы без задержек. Технологии отлажены, процессы оптимизированы. Поэтому вы получите свой заказ в установленный срок и надлежащего качества.
 Чтобы вы получили его без задержек, в штате работают более 50 человек, каждый из которых профи. Доставляем по Москве и Московской области.
Чтобы вы получили его без задержек, в штате работают более 50 человек, каждый из которых профи. Доставляем по Москве и Московской области. - Продаем не только типовые изделия. Работаем в индивидуальном порядке, воплотим вашу идею в жизнь.
- Специалисты успешно сочетают древние традиции и современные технологии, от чего вы получаете эксклюзивные изделия высокого качества.
- Используем пескоструйную обработку, благодаря которой срок эксплуатации увеличивается в 1,5 раза.
- Скорее всего, вы о нас уже слышали. Работаем более 10 лет. О нашей качественной работе говорят отзывы довольных покупателей.
- Типовые варианты мы можем изготовить в течение 48 часов в срочном порядке. Производство дизайнерских решеток занимает обычно 7-14 дней. В остальном срок зависит от объема партии.
- Стоимость прописывается в договоре и не меняется в процессе установки. Вы знаете точную цену, которая точно не изменится.
- Кроме покупки решетки вы сразу можете воспользоваться всеми сопутствующими услугами: отрисовкой эскиза решетки, покраской, доставкой, демонтажем предыдущей решетки и, конечно же, установкой.
 Гарантия распространяется на все виды решеток и на установку.
Гарантия распространяется на все виды решеток и на установку. - Вы получите аккуратную и чистую работу, строительный мусор вывезем самостоятельно.
- Доставка и установка решеток каждому клиенту в подарок!
Работаем в Москве
Замер
Выезд замерщика бесплатный. Наш специалист измерит оконные проемы, покажет полный каталог эскизов, поможет с подбором
и рассчитает точную стоимость оконных решеток. Вызвать замерщика.
Доставка и установка
Стоимость доставки зависит от удаленности. По Москве доставка бесплатная. Доставка в Москве уточняйте по телефону. Подробные тарифы смотрите на странице доставка. Установка производится в день доставки.
Оплата
Оплата производится в 2 этапа:
- Предоплата 30% после замера и заключения договора;
- Остаток 70% вы оплачиваете после установки решеток.
Принимаем к оплате как наличные, так и безналичные переводы.
Чтобы заказать решетки на окна с установкой, свяжитесь с нами по телефону 8 800 600 78 14 +7 495 231-90-00
оконная решетчатая решетка — 7 для продажи на 1stdibs
Расположение предмета
Сортировка на
Рекомендуемое Newestrelevanceprice: High — Lowprice: Low — Highpopular
решетчатая оконная панель, вероятно, возникла в северном китайском доме с нейтральным и сбалансированным интерьером. Геометрический решетчатый узор является линейным и открытым, и…
Геометрический решетчатый узор является линейным и открытым, и…
Категория
Китайские настенные скульптуры Цин начала 20-го века
Материалы
Pine
Панель из китайской решетки, около 1900
H 44,75 дюйма W 37 дюймов D 1,25 дюйма. Эта решетчатая оконная панель начала 20-го века, вероятно, возникла в северном китайском доме с нейтральным и сбалансированным интерьером. Геометрический решетчатый узор является линейным и открытым, и…
Категория
Китайские настенные скульптуры Цин начала 20-го века
Материалы
Pine
Панель из китайской решетки, около 1900
H 44,5 дюйма W 37 дюймов D 1,5 дюйма.
Эта решетчатая оконная панель начала 20-го века, вероятно, возникла в северном китайском доме с нейтральным и сбалансированным интерьером. Геометрический решетчатый узор является линейным и открытым, и…
Геометрический решетчатый узор является линейным и открытым, и…
Категория
Китайские настенные скульптуры Цин начала 20-го века
Материалы
Сосновая
Панель из китайской алмазной решетки, около 1900
H 42,25 дюйма W 52,25 дюйма D 1,25 дюйма
Китайская лат -панель с латтизмом Chrysanthem, Circa 1900
Эта решетчатая оконная панель начала 20-го века из китайской провинции Шаньси, вероятно, возникла в традиционном доме со сбалансированным интерьером. Как функциональные, так и декоративные, решетчатые …
Категория
Китайские настенные скульптуры Цин начала 20 века
Материалы
Сосновая
КИТАЙНА
Пара деревянных оконных панелей или решеток в китайском стиле с геометрической решеткой. Врезные и шиповые столярные изделия с окрашенной отделкой и китайской письменностью на одной двери, как видно из. ..
..
Категория
Китайский экспорт 20-го века Еще Азиатское искусство, предметы и мебель
Материалы
Дерево
Пара китайских оконных панелей с геометрической решеткой
В 72,5 дюйма Ш 27,5 дюйма Г 1,5 дюйма
Характерная пара китайских резных дверей с решетчатыми окнами в виде открытой лепнины. Толстые рамы имеют старинные врезные и шиповые столярные изделия. Высота более 9,5 футов…
Категория
Китайская мебель династии Мин 20-го века
Материалы
Дерево
Пара китайских резных дверей с решетчатыми окнами
В 114,5 дюйма Ш 20,5 дюйма Г 2,5 дюйма IL
Треугольная решетчатая оконная панель из загородного клуба Oak Park, около 1914 года.0023 Решетчатая оконная панель из загородного клуба Oak Park
В 41 дюйм Ш 24,5 дюйма Г 1 дюйм
Набор из шести старинных решетчатых оконных панелей Мин, XIX век
Находится в Сомис, Калифорния
Эти красивые оконные сетки являются прекрасным примером простого элегантного стиля домашнего интерьера династии Мин. Линии формируются кропотливо вручную с помощью традиционной столярной мастерской.0016
Линии формируются кропотливо вручную с помощью традиционной столярной мастерской.0016
Материалы
Дерево
Набор из шести старинных решетчатых оконных панелей династии Мин, 19 век
В 65 дюймов Ш 20 дюймов Г 2 дюйма Чикаго, Иллинойс
Пара оконных решетчатых панелей из китайского вяза XIX века с цветочным узором. Красная коллекция пагоды #: CAI082 Ключевые слова: решетка, окно, панель, архитектурная, дверь
Категория
Антично китайские окна 19 -го века
Материалы
ELM
Пара китайского окна 19 -го века
H 45 дюймов. W 44,5 дюйма D 1,5 дюйма
Пара оконных решетча в Чикаго, Иллинойс
Пара оконных решетчатых панелей из китайского камфорного дерева XIX века с вырезанными кривыми мотивами дракона и феникса на зеркалах.
Пагода Красная Коллекция #: CAE103<...
Категория
Старинные настенные зеркала XIX века
Пара оконных решетчатых панелей с зеркалами
В 29 дюймов Ш 22 дюйма Г 1 дюйм Чикаго, Иллинойс
Китайское оконное решетчатое зеркало начала 20 века с переплетенными кольцами и бриллиантами. Красная коллекция пагоды #: Z174E Ключевые слова: Зеркало, окно, решетка, картина, настенный…
Категория
Настенные зеркала начала 20 века
Китайская оконная решетка начала 20 века с зеркалом
В 23 дюйма Ш 39 дюймов Г 1,5 дюйма
Зеркало начала 20 века 3 Китайское окно 9000 9000 в Чикаго, Иллинойс
Китайская оконная решетка начала 20-го века с резными цветами лотоса и зеркалом. Красная коллекция пагоды #: Z174B Ключевые слова: Зеркало, настенная подвеска, картина, фото. ..
..
Категория
начало 20 -го века китайские настенные зеркала
Материалы
Glass, ELM
РАННЯЯ КИТАЙСКА Китайская оконная решетка с зеркалом
Расположена в Чикаго, штат Иллинойс
Китайская зеркальная оконная решетка начала 20-го века с декоративными элементами, вырезанными в виде бабочек.
Пагода Красная Коллекция #: Зеркало, панно, картина, фотография, настенный га…
Категория
Стенные зеркала начала 20 -го века
Материалы
FIR
РАННЯЯ КИТАЙСКАЯ ОКЛОВАЯ РАБОТА С Зеркалом
H 32 дюйма. с зеркалом
Находится в Чикаго, штат Иллинойс.
Китайская оконная решетка начала 20-го века с резными цветочными деталями и зеркалом. Красная коллекция пагоды #: Z174D Ключевые слова: Зеркало, панно, картина, фотогр. ..
..
Категория
Стенные зеркала начала 20-го века
Материалы
FIR
РАННЯЯ КИТАЙНАЯ ВЕЛИКА Китайская оконная решетчатая решетка с зеркалом
H 32 дюйма W 35 дюймов D 1,5 дюйма
ELM ELM Windenel окна Решетчатые двери-ширмы, провинция Шаньси
Расположен в Лондоне, GB
Китайский вяз, восьмипанельные окна, решетчатые двери-ширмы из провинции Шаньси, 19 век, с круглыми железными ручками.
Категория
Антиквариат 19Китайские картины и ширмы
Восьмипанельные оконные решетки из китайского вяза, провинция Шаньси
В 90,6 дюйма, Ш 170 дюймов, Г 1,5 дюйма
Китайская оконная решетка начала 20 века с зеркалом
2 Расположен в Чикаго, IL
Китайская оконная решетка начала 20-го века с резными картушами в цветочном стиле и зеркалом. Красная коллекция пагоды #: Z174G Ключевые слова:
Зеркало, панно, картина, фото…
Красная коллекция пагоды #: Z174G Ключевые слова:
Зеркало, панно, картина, фото…
Категория
Стенные зеркала начала 20 -го века
Материалы
FIR, стекло
Раннее 20 -е век китайскую оконную панель с зеркалом
H 26,5 дюйма W 36 дюйма D 1,75 дюйма
Китайская оконная решетчатая панель с зеркалом
Расположена в Чикаго, штат Иллинойс.
Китайская оконная решетчатая панель начала 20-го века со стилизованным мотивом бабочки и зеркалом. Красная коллекция пагоды #: Z174J Ключевые слова: Зеркало, панно, картина,…
Категория
Антиквариат 19-го века Еще азиатское искусство, предметы и мебель
Китайская оконная решетка начала 20-го века с зеркалом
В 30 дюймов Ш 35 дюймов Г 1,5 дюйма Век
Пара Оконные решетки
Находится в Чикаго, штат Иллинойс.
Пара оконных панелей из китайского вяза XIX века с резной решеткой в цветочек. Красная коллекция пагоды #: CAI072A Ключевые слова: Решетка, панно, панно, картина, фотография
Категория
Скульптуры 19 -го века
Материалы
ELM
Пара китайского цветочного окна 19 -го века
H 27 дюймов. Окно с зеркалом
Находится в Чикаго, штат Иллинойс.
Китайская оконная решетка 19-го века с резными бабочками и геометрическими фигурами, подкрепленная зеркалом. Красная коллекция пагоды #: Z174H Ключевые слова: Зеркало, рама
Категория
Начало 20 -го века Металлические изделия
Материалы
FIR, стекло
РАННОЕ 20 -й век китайский бабочка .
Находится в Нью-Йорке, штат Нью-Йорк
Решетчатая панель из кедрового дерева из провинции Чжэцзян, конец 19 века.
Категория
Старинное китайское декоративное искусство XIX века
Китайская решетчатая оконная панель.
В 39 дюймов Ш 35 дюймов Г 2 дюйма
Китайская решетчатая оконная панель
Расположенная в Чикаго, Иллинойс
Элегантная в своей простоте эта решетчатая оконная панель 19-го обеспечение определенной степени конфиденциальности. В отличие от резьбы или перфорации дерева…
Категория
Антикварная китайская мебель Цин середины XIX века
Материалы
Пихта
Китайская решетчатая оконная панель
В 84 дюйма Ш 30,5 дюйма Г 2,25 дюйма
Зеркало из китайской решетчатой оконной панели
Расположено в Чикаго, Иллинойс
Эта решетчатая оконная панель, вероятно, возникла в аристократическом китайском доме с нейтральным и гармоничным интерьером. Геометрический узор решетки является линейным и открытым, и был разработан или…
Геометрический узор решетки является линейным и открытым, и был разработан или…
Категория
Китайские настенные зеркала Qing начала 20-го века
Материалы
Кедр, зеркало
Китайская решетчатая оконная панель Зеркало
В 59,75 дюйма Ш 43,75 дюйма Г 2 дюйма
Китайская решетчатая оконная панель, около 1900 г.
Находится в Чикаго, Иллинойс
сбалансированный интерьер. Геометрический решетчатый рисунок является линейным и открытым, с…Категория
Китайские настенные скульптуры Цин начала 20-го века
Материалы
Сосна
Китайская решетчатая оконная панель, около 1900
В 42,5 дюйма Ш 52 дюйма Г 1,25 дюйма
Китайская решетчатая оконная панель, около 1900 г. и сбалансированный интерьер. Геометрический решетчатый рисунок является линейным и открытым, с…
Геометрический решетчатый рисунок является линейным и открытым, с…
Категория
Китайские настенные скульптуры Цин начала 20-го века
Материалы
Сосна
Китайская решетчатая оконная панель, около 1900
В 47,5 дюйма Ш 40,25 дюйма Г 1,25 дюйма
Китайская решетчатая оконная панель зеленого цвета
Находится в Чикаго, Иллинойс
Эта решетчатая оконная панель, вероятно, возникла в аристократическом китайском доме с нейтральным и гармоничным интерьером. Геометрический рисунок решетки является линейным и открытым, и был разработан или…
Категория
Китайский лак Цин начала 20-го века
Материалы
Кедр
Китайский зеленый лак Решетчатая оконная панель
В 59,75 дюйма Ш 43,75 дюйма Г 2 дюйма
Китайская решетчатая оконная панель, около 1900 г.
Находится в Чикаго, Иллинойс
сбалансированный интерьер. Геометрический решетчатый рисунок является линейным и открытым, с…Категория
Китайские настенные скульптуры Цин начала 20-го века
Материалы
Сосна
Китайская решетчатая оконная панель, около 1900
В 50,25 дюйма Ш 37,5 дюйма Г 1,25 дюйма
Китайская решетчатая оконная панель, около 1900 г. и сбалансированный интерьер. Геометрический решетчатый рисунок является линейным и открытым, с…
Категория
Китайские настенные скульптуры Цин начала 20-го века
Материалы
Сосна
Китайская решетчатая оконная панель, около 1900
В 41,5 дюйма Ш 53,75 дюйма Г 1,25 дюйма
Китайская решетчатая оконная панель, около 1900 г. и сбалансированный интерьер. Геометрический решетчатый рисунок является линейным и открытым, с…
и сбалансированный интерьер. Геометрический решетчатый рисунок является линейным и открытым, с…
Категория
Китайские настенные скульптуры Цин начала 20-го века
Материалы
Сосна
Китайская решетчатая оконная панель, около 1900
В 47,25 дюйма Ш 43,5 дюйма Г 1,5 дюйма
Китайская решетчатая оконная панель, около 1900 г. нейтральный и сбалансированный интерьер. Геометрический решетчатый рисунок является линейным и открытым, и имеет…
Категория
Китайские настенные скульптуры Цин начала 20-го века
Материалы
Сосна
Китайская алмазная решетчатая оконная панель, около 1900
В 37,75 дюйма Ш 45,5 дюйма Г 1,25 дюйма
Китайская решетчатая оконная панель, около 1900 г. нейтральный и сбалансированный интерьер. Геометрический решетчатый узор является линейным и открытым, и…
нейтральный и сбалансированный интерьер. Геометрический решетчатый узор является линейным и открытым, и…
Категория
Китайские настенные скульптуры Цин начала 20-го века
Материалы
Сосна
Оконная панель с китайской алмазной решеткой, около 1900 г.
В 42,5 дюйма, Ш 47,25 дюйма, Г 1,5 дюйма
Оконная панель с китайской алмазной решеткой, около 1900 г. вероятно, возник в северном китайском доме с нейтральным и сбалансированным интерьером. Геометрический решетчатый узор является линейным и открытым, и…
Категория
Китайские настенные скульптуры Цин начала 20-го века
Материалы
Сосновая
Панель из китайской алмазной решетки, около 1900
H 51,75 дюйма. решетчатая оконная панель, вероятно, возникла в аристократическом китайском доме с нейтральным и сбалансированным интерьером. Замысловатая решетчатая конструкция была разработана для того, чтобы впустить свет и воздух в …
Замысловатая решетчатая конструкция была разработана для того, чтобы впустить свет и воздух в …
Категория
Антиквариат середины 19-го века Китайский Цин Еще Азиатское искусство, предметы и мебель
Материалы
Вяз
Китайская цветочная решетчатая оконная панель 19-го века
В 36,5 дюйма Ш Г 36,5 дюйма 2 дюйма CT
Изящный набор из четырех оконных панелей с геометрической решетчатой резьбой. Посетите наш веб-сайт по адресу: www.greenwichorientalantiques.com для выбора дополнительных «аксессуаров».
Категория
Старинное китайское декоративное искусство XIX века
Набор из четырех оконных панелей с решетчатой резьбой
Высота 61 дюйм, ширина 18,5 дюйма, глубина 2 дюйма
Шестиугольный садовый фонарь из японского кедра с решетчатыми окнами, период Мэйдзи
Японский садовый фонарь шестиугольной формы, изготовленный из кедра, подвергшегося влиянию ветра и дождя, чтобы образовалась самая приятная на ощупь патина под древесину, которая придает внешнему. ..0016
..0016
Материалы
Iron
Японский шестиугольный садовый фонарь с решетчатыми окнами, период Meiji
H 11,82 дюйма. Решетчатая панель окна из китайского кипариса начала 20 века, изображающая стилизованный повторяющийся мотив цветка хризантемы. Красная коллекция пагоды #: BJB119E Ключевые слова: Решетка, панель…
Категория
20 -го века китайские рисунки и экраны
Материалы
Cypress
Раннее 20 -е век китайская оконная решетчатая панель
H 49 дюймов Wecond. W 54,5 дюйма. D 1,5 дюйма
Расположен в Вашингтоне, округ Колумбия
Окна с окрашенными решетчатыми решетками из кованого железа
Категория
Старинные французские настенные зеркала конца XIX века
Материалы
Кованое железо
Окрашенная решетчатая решетка из кованого железа Зеркальные окна
В 37,50 дюйма Ш 31,75 дюйма Г 1,75 дюйма вероятно. в аристократическом китайском доме с нейтральными и уравновешенными интерьерами. Геометрический узор решетки является линейным и открытым, и был разработан или…0016
в аристократическом китайском доме с нейтральными и уравновешенными интерьерами. Геометрический узор решетки является линейным и открытым, и был разработан или…0016
Материалы
CEDAR
КИТА -ЗЕЛЕНЫ Эта решетчатая оконная панель начала 20-го века, вероятно, возникла в северном китайском доме с нейтральным и сбалансированным интерьером. Геометрический решетчатый узор является линейным и открытым, и…
Категория
Китайские настенные скульптуры Цин начала 20-го века
Материалы
Сосновая
Панель из китайской алмазной решетки, около 1900
H 54,5 дюйма W 47,5 дюйма D 1,25 дюйма
Компания Windate Windate Windate, Circa 1900
, расположенная в Chicago, il
Эта решетчатая оконная панель начала 20-го века, вероятно, возникла в северном китайском доме с нейтральным и сбалансированным интерьером. Геометрический решетчатый узор является линейным и открытым, и…
Геометрический решетчатый узор является линейным и открытым, и…
Категория
Китайские настенные скульптуры Цин начала 20-го века
Материалы
Сосна
Китайская решетчатая оконная панель, около 1900 г.
В 44 дюйма Ш 47 дюймов Г 1,75 дюйма CA
Собранный набор из четырех китайских оконных панелей с геометрической открытой резной решеткой. Аналогичные по размеру с одной узкой 18-дюймовой панелью и одной короткой 51-дюймовой панелью. Может быть, мы…
Категория
Китайский Мин 20-го века Еще Азиатское искусство, предметы и мебель
Материалы
Дерево
Набор из четырех китайских оконных панелей с геометрической решеткой
В 54 дюйма Ш 21 дюйм Г 1 дюйм 1900
Расположенная в Чикаго, штат Иллинойс, штат Иллинойс.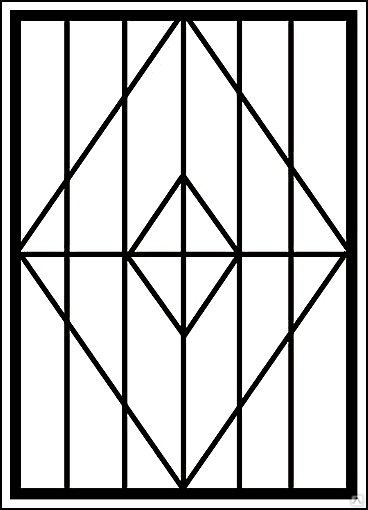
Эта пара богато украшенных оконных панелей, украшенных кроваво-красным лаком и оригинальной золотой краской, является прекрасным примером традиционной китайской решетки. Встраивается в стену или дверь…
Категория
Антиквариат Конец 19Китайский цинский древний век
Материалы
Тик
Пара оконных панелей из китайской позолоты, ок. 1900
В 32 дюйма Ш 39,5 дюймов Г 2 дюйма
резная деревянная оконная решетка
Расположено в Бруклине, штат Нью-Йорк
прекрасное резное деревянное окно. Сделанный из цельного куска вяза, его можно переустановить в интерьере или просто повесить как произведение искусства.
Категория
Старинное китайское декоративное искусство XIX века
Материалы
Дерево
оконная решетка из резного дерева
В 37 дюймов Ш 19,5 дюймов Г 1 дюйм
Категория
Винтаж 1950S Китайские Windows
Материалы
Wood
РАЗРЕШЕНИЯ ОКРЫВАЙСТВА
H 92 дюйма. 0003
0003
Китайская решетчатая оконная панель минимального геометрического дизайна. Бледная, сырая хвойная древесина.
Категория
20 -й век китайские окна
Материалы
СОВЕРКА
БЕСПЛАТНАЯ ПАНЕЛА РАЗРЕШЕНИЯ
H 52 дюйма. Китайская решетчатая оконная панель минимального геометрического дизайна. Бледная сырая хвойная древесина.
Категория
Китайские окна 20-го века
Материалы
Софта
Отделенная решетчатая панель
H 54 дюйма. . Рамка со скошенными углами и вставкой из сетки.
Категория
Китайские ширмы и перегородки ХХ века
Материалы
Дерево
Китайская решетчатая оконная ширма
В 92 дюйма Ш 35,5 дюйма Г 2 дюйма
Пара китайских решетчатых оконных панелей
Расположен в Вашингтоне, округ Колумбия
Две прямоугольные панели с геометрическими решетчатыми вставками в рамке, каждая с декоративной латунной подвеской.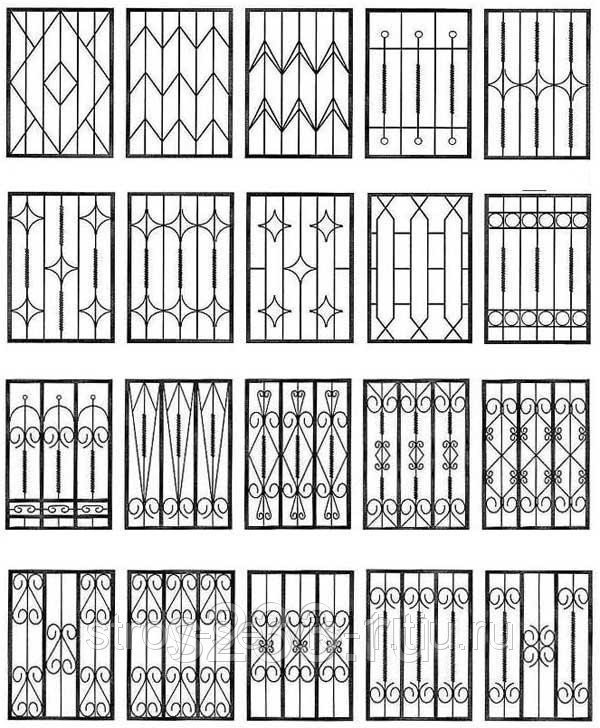
Категория
Античный китайский декоративное искусство 19 -го века
Материалы
Латунь
Пара оконных решетчатых панелей
H 35,5 дюйма W 17,5 дюйма D 1,25 дюйма
19 -й век.0003
Расположен в Нью-Йорке, штат Нью-Йорк.
Большая резная оконная панель из китайского дерева с решетчатым узором.
Категория
Античные китайские рисунки и экраны 19 -го века
Материалы
Wood
19 -й век китайская решетчатая панель
H 53 дюйма. Century
Расположен в Сарасоте, Флорида
Прекрасные резные китайские окна. Можно встроить в стену или повесить декоративно. Потрясающий пример тонкой решетчатой работы.
Категория
Антично 1890S китайские китайские скульптуры и резьбы китайского чиппендейла
Материалы
Дерево
Китайская решетчатая фретка Резное панно XIX века
Расположено в Сарасоте, Флорида
Прекрасное резное китайское окно. Можно встроить в стену или повесить декоративно. Потрясающий пример тонкой решетчатой работы.
Можно встроить в стену или повесить декоративно. Потрясающий пример тонкой решетчатой работы.
Категория
Антично 1890S Китайские китайские экспортные скульптуры и резьбы
Материалы
Wood
Новые поступления
Сохраните «Оконная решетка», и мы сообщим вам, когда появятся новые объявления в этой категории.
Оконная решетка для продажи на 1stDibs
Найдите множество разновидностей аутентичных оконных решеток, доступных на 1stDibs. Оконная решетка, часто сделанная из дерева, хвойных пород и сосны, может поднять любой дом. Ваша гостиная может быть неполной без оконной решетки — найдите в продаже старые выпуски от 19th Century и более новые версии, сделанные совсем недавно, в 20-м веке. Оконная решетка – предмет мебели в целом популярный, но и те, что созданы в стилях, пользуются спросом часто.
Сколько стоит оконная решетка?
Цены на оконные решетки могут различаться в зависимости от размера, периода времени и других атрибутов — на 1stDibs они начинаются с 750 долларов и могут доходить до 5600 долларов, а в среднем могут достигать 1680 долларов.
Дополнительные способы просмотра
Окно с зеркалом
китайское окно с решеткой
Старинные стеклянные зеркальные панели
Чин Art
Китайская панель с резьбой по дереву
Экраны Дверные панели
Посмотреть все популярные поисковые запросы мебели
Что такое решетчатое окно?
`;
Термин «решетчатое окно» относится к типу окна, которое имеет ряд прямых или изогнутых стержней, которые используются для удерживания небольших кусочков стекла. Эти стержни могут быть изготовлены из дерева или металла. В некоторых случаях перекладины функциональны и удерживают на месте несколько квадратных или прямоугольных оконных стекол. В других случаях металлические или деревянные перерывы в решетчатом окне носят чисто декоративный характер.
В некоторых местах вместо решетчатого окна будет использоваться решетчатая панель. Решетчатая панель – это решетчатое окно без стекла. Это обычное явление во внешних коридорах и в регионах с умеренным климатом.
В зависимости от конструкции решетчатого окна узор, создаваемый в оконной раме, может быть очень простым или невероятно подробным. Примером простого дизайна может быть узор из перекрещивающихся стержней, которые создают ромбовидные секции стекла внутри оконной рамы. Более сложный дизайн может включать в себя множество кусочков стекла разных форм и размеров, которые вписываются в изгибы и завитки решетки. Чем сложнее конструкция в решетчатом окне, тем труднее ее выполнить. Эти более сложные конструкции также обычно дороже, чем более простые разновидности.
Более сложный дизайн может включать в себя множество кусочков стекла разных форм и размеров, которые вписываются в изгибы и завитки решетки. Чем сложнее конструкция в решетчатом окне, тем труднее ее выполнить. Эти более сложные конструкции также обычно дороже, чем более простые разновидности.
Решетчатые окна веками использовались в архитектуре. Различные конструкции, которые используются до сих пор, уходят своими корнями в древность. Людям, занимающимся реставрацией старых зданий, часто приходится заменять решетчатые окна. Иногда можно воссоздать окна, которые были оригинальными для конструкции, или найти почти идентичные старинные решетчатые окна, которые были спасены из подобных зданий. В других случаях оригинальное решетчатое окно должно быть аппроксимировано новой моделью, которая не является аутентичной, но часто является более доступным вариантом.
В других случаях оригинальное решетчатое окно должно быть аппроксимировано новой моделью, которая не является аутентичной, но часто является более доступным вариантом.
Решетчатые окна также используются при проектировании новых конструкций. Это верно для ряда видов сооружений, включая частные дома и места отправления культа. Дизайн в кадре в определенной степени прерывает вид, но иногда это делается намеренно. Очень сложный дизайн в решетчатом окне может обеспечить определенную степень конфиденциальности. Это может быть полезно для окон, которые находятся на уровне улицы здания.
В дополнение к своей работе в качестве внештатного автора для HomeQuestionsAnswered, Дайан является исполнительным редактором Black Lawrence Press, независимое издательство, базирующееся в северной части штата Нью-Йорк. Она также редактировала несколько антологии, электронный информационный бюллетень Sapling и The Adirondack Review. Дайан имеет степень бакалавра. из колледжа Сары Лоуренс и степень магистра Бруклинского колледжа.
Дайан Геттель В дополнение к своей работе в качестве внештатного автора для HomeQuestionsAnswered, Дайан является исполнительным редактором
Black Lawrence Press, независимое издательство, базирующееся в северной части штата Нью-Йорк. Она также редактировала несколько
антологии, электронный информационный бюллетень Sapling и The Adirondack Review. Дайан имеет степень бакалавра. из колледжа Сары Лоуренс и
степень магистра Бруклинского колледжа.
Она также редактировала несколько
антологии, электронный информационный бюллетень Sapling и The Adirondack Review. Дайан имеет степень бакалавра. из колледжа Сары Лоуренс и
степень магистра Бруклинского колледжа.
Многооконный поиск фазы STFT: уникальность решетки — arXiv Vanity
Philipp Grohs * , † , ‡ * Факультет математики Венского университета, Oskar-Morgenstern-Platz 1, 109 Austria † Research Network [адрес электронной почты защищен], Венский университет, Колингассе 14-16, 1090 Вена, Австрия ‡ Институт прикладной и вычислительной математики имени Иоганна Радона Австрийской академии наук, Альтенбергштрассе 69, 4040 Линц, Австрия § Институт математики Бордо, Университет Бордо, UMR CNRS 5251, 351 Cours de la Libération 33405, Таланс, Франция , Лукас Лиер * а также Мартин Ратмайр §
30 июля 2022 г.
Аннотация.
Восстановление фазы с помощью кратковременного преобразования Фурье (STFT) относится к восстановлению сигнала f по его спектрограмме, т. е. величин его STFT
| Vgf(x,ω):=∫Rf(t)¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯g(t−x)e−2πitωdt, |
и является центральной проблемой в нескольких приложениях, включая когерентную дифракционную визуализацию и обработку звука. Известно, что для нескольких оконных функций g любую функцию f∈L2(R) можно восстановить по полной спектрограмме |Vgf(R2)| но на практике реконструкцию необходимо проводить только по дискретным образцам |Vgf(Λ)|, обычно по решетке Λ=AZ2. Оказывается, проблема выборки становится намного более тонкой:
Недавно установленные барьеры дискретизации заявляют, что уникальность с помощью решеточной выборки никогда не достижима в L2(R), независимо от оконной функции g и плотности решетки.
Поэтому в настоящей статье мы инициируем исследование извлечения фазы многооконного STFT. Мы обнаруживаем новую связь между многооконным поиском фазы STFT и выборкой в пространстве Фока, что позволяет нам установить результаты уникальности по восстанавливаемости функций, интегрируемых с квадратом, из выборок спектрограмм, расположенных на решетках. А именно, мы задаем условия на оконные функции g1,…,g4∈L2(R) такие, что каждая f∈L2(R) с точностью до глобальной фазы определяется
Мы обнаруживаем новую связь между многооконным поиском фазы STFT и выборкой в пространстве Фока, что позволяет нам установить результаты уникальности по восстанавливаемости функций, интегрируемых с квадратом, из выборок спектрограмм, расположенных на решетках. А именно, мы задаем условия на оконные функции g1,…,g4∈L2(R) такие, что каждая f∈L2(R) с точностью до глобальной фазы определяется
| (|Vg1f(AZ2)|,…,|Vg4f(AZ2)|) |
всякий раз, когда A∈GL2(R) удовлетворяет условию плотности |detA|−1≥4. Для вещественных сигналов f∈L2(R,R) достаточно, чтобы |detA|−1≥2. Также показаны соответствующие результаты для нерегулярной выборки. Таким образом, наши результаты преодолевают вышеупомянутые барьеры дискретизации и представляют собой первый общий результат уникальности для выборочного извлечения фазы STFT.
Ключевые слова. фазовый поиск, выборка, частотно-временной анализ, пространство Фока, решетки, многооконный анализ Габора
Тематические классификации AMS. 30х30, 46Е22, 94А12, 94А20
30х30, 46Е22, 94А12, 94А20
1. Введение
Проблема восстановления функции по ее спектрограмме, т. е. абсолютного значения ее кратковременного преобразования Фурье (STFT), является ключевым шагом в нескольких важных прикладных задачах, представляющих интерес в настоящее время, которые варьируются от когерентной дифракционной визуализации по сравнению с обработкой звука до квантовой обработки. механика. Полученная обратная задача широко известна как задача восстановления фазы STFT. Повсеместный характер проблемы восстановления фазы STFT и ее актуальность для многих субъектов привели к интенсивным исследованиям в последние годы, см., например, [2, 17, 15, 14, 16] и ссылки в нем. Короче говоря, эта задача требует инвертировать карту
| f↦|Vgf(Λ)|\coloneqq(|Vgf(z)|)z∈Λ |
, который переводит на свою спектрограмму |Vgf| интегрируемую с квадратом функцию f∈L2(R) выборка на Λ⊆R2. Отображение Vgf обозначает кратковременное преобразование Фурье f относительно оконной функции g∈L2(R) и определяется как
Отображение Vgf обозначает кратковременное преобразование Фурье f относительно оконной функции g∈L2(R) и определяется как
| (1) | Vgf(x,ω)=∫Rf(t)¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯g(t−x)e−2πitωdt,x,ω∈R. |
Обратите внимание, что умножение f на комплексный скаляр единичного модуля не меняет соответствующую спектрограмму, и поэтому реконструкция возможна только с точностью до неоднозначности глобального фазового коэффициента. Классическим результатом является то, что мягкие предположения об оконной функции g подразумевают, что каждая функция f∈L2(R) определяется (с точностью до глобальной фазы) |Vgf(Λ)| при условии, что Λ=R2.
В практических приложениях доступны только образцы спектрограммы. Поэтому крайне важно определить, в какой степени утверждения единственности из Λ=R2 переходят в утверждения единственности из дискретных множеств выборки Λ, особенно решеток, т. е. Λ=AZ2 для некоторой обратимой матрицы A∈GL2(R). К сожалению, недавно в [13, 3, 12] было показано, что реконструкция по образцам решетки невозможна:
К сожалению, недавно в [13, 3, 12] было показано, что реконструкция по образцам решетки невозможна:
не существует оконной функции и такой решетки Λ, что каждая f∈L2(R) с точностью до глобальной фазы определяется |Vgf(Λ)|.
Следовательно, выборка на решетках не приводит к дискретизации задачи восстановления фазы STFT, независимо от того, насколько плотная решетка выбрана. Обратите внимание, что это резко контрастирует с ситуацией, когда присутствует информация о фазе, поскольку классические результаты частотно-временного анализа демонстрируют стабильное восстановление любого f∈L2(R) из Vgf(AZ2) при условии, что AZ2 подчиняется подходящему условию плотности.
Поскольку приложения требуют возможности восстановления на основе выборочных измерений, вопрос о том, как адаптировать процедуру регистрации сигнала, чтобы гарантировать уникальность выборок, имеет первостепенное значение.
В настоящей статье мы предлагаем увеличить избыточность измерений помимо измерений на решетке, возникающих из-за единственной оконной функции. Мы используем многооконный подход, который хорошо зарекомендовал себя в анализе Габора 9.1111 [5, 10] , чтобы преодолеть барьеры дискретизации, присутствующие в ситуации «единого окна», и показать, что
Мы используем многооконный подход, который хорошо зарекомендовал себя в анализе Габора 9.1111 [5, 10] , чтобы преодолеть барьеры дискретизации, присутствующие в ситуации «единого окна», и показать, что
существуют оконные функции g1,g2,g3,g4 такие, что для каждого A∈GL2(R) с |det(A)|−1李4 каждая f∈L2(R) определяется с точностью до глобальной фазы по
(|Vg1f(AZ2)|,…,|Vg4f(AZ2)|).
Оконные функции имеют довольно простую форму, так как они могут быть выбраны как линейные комбинации
гауссиана и первая функция Эрмита. Таким образом, наши результаты показывают, что выборки спектрограмм по четырем оконным функциям содержат достаточно информации для восстановления любой интегрируемой с квадратом комплексной функции. Напротив, предыдущие результаты показали, что единственность решетки возможна только при жестких ограничениях класса сигналов подпространствами L2(R) [11] . Теоремы построены таким образом, что они дают легко проверяемое условие на g1,…,g4, такое, что гарантируется уникальное восстановление с помощью бесфазовой выборки. Кроме того, операторы гибки для получения результатов бесфазной выборки из неоднородных наборов выборки, отличных от решеток (см. теорему 4.3 в разделе 4).
Насколько нам известно, эти результаты представляют собой первый в истории результат уникальности для извлечения фазы STFT из дискретных и разделенных образцов.
Теоремы построены таким образом, что они дают легко проверяемое условие на g1,…,g4, такое, что гарантируется уникальное восстановление с помощью бесфазовой выборки. Кроме того, операторы гибки для получения результатов бесфазной выборки из неоднородных наборов выборки, отличных от решеток (см. теорему 4.3 в разделе 4).
Насколько нам известно, эти результаты представляют собой первый в истории результат уникальности для извлечения фазы STFT из дискретных и разделенных образцов.
Напомним, что существует однозначное соответствие между STFT с гауссовыми окнами и функциями в пространстве Баргмана-Фока. Несмотря на то, что пространства Фока содержат богатую теорию уникальности, выборки и интерполяции, эта теория до сих пор не играла сколько-нибудь существенной роли в изучении задачи восстановления фазы STFT. Методы доказательства, представленные в настоящем изложении, демонстрируют, что многооконный подход открывает дверь для применения результатов выборки в пространствах Фока к проблеме бесфазной выборки STFT, подчеркивая основную связь между двумя объектами и представляя первый шаг в представить литературу по переходу от классической выборки STFT к бесфазной выборке STFT.
1.1. Взносы
Мы считаем элементы f,h векторного пространства над комплексным полем C эквивалентными и пишем f∼h, если существует константа τ∈T\coloneqq{z∈C:|z|=1} такая, что f=τh . Если f ∼h, то мы также говорим, что f и h согласуются с точностью до глобальной фазы. Следующее определение устанавливает нотацию многооконного поиска фазы STFT.
Определение 1.1.
Пусть I — множество индексов, пусть {gp}p∈I⊆L2(R) — семейство оконных функций, пусть Λ⊆R2 — множество точек дискретизации, а C⊆L2(R) — класс сигналов. Мы говорим, что ({gp}p∈I,Λ) выполняет поиск фазы на C, если он содержит это
| (f,h∈C: |Vgpf(Λ)|=|Vgph(Λ)|, ∀p∈I)⟹f∼h. |
Немного злоупотребляя обозначениями, мы будем говорить, что семейство векторов V⊆Cn выполняет фазовый поиск, если оно содержит
| (z,w∈Cn: |⟨z,φ⟩|=|⟨w,φ⟩|, ∀φ∈V)⟹z∼w. |
Имея под рукой изложенную выше терминологию, мы можем теперь перейти к обсуждению основных результатов статьи. Для этого напомним, что первые два Функции Эрмита h0,h2∈L2(R) задаются как
Для этого напомним, что первые два Функции Эрмита h0,h2∈L2(R) задаются как
| h0(t)=21/4e−πt2, h2(t)=25/4πte−πt2. |
Мы будем использовать оконные функции, которые возникают как линейные комбинации h0 и h2, и определим
| (2) | gp:=λh0+µh2,p=(λ,µ)∈C2. |
Это приводит к семейству оконных функций {gp}⊆L2(R), параметризуемых p∈C2. Мы называем p∈C2 определяющим вектором gp. Теперь рассмотрим подмножество P⊆C2 и будем считать P набором индексов. Следующее утверждение раскрывает связь между поиском фазы в C2 и многооконным поиском фазы STFT. В ситуации, когда сигнальное пространство C состоит из всего пространства L2(R), решеточная версия этого утверждения читается следующим образом.
Теорема 1.2.
Предположим, что P⊆C2 выполняет восстановление фазы.
Если A∈GL2(R) удовлетворяет условию |det(A)|−1李4, то ({gp}p∈P,AZ2) выполняет поиск фазы на L2(R).
В ограниченных условиях, когда предполагается, что пространство сигналов состоит только из вещественных функций (C=L2(R,R)), достижимо уменьшение плотности точек выборки наполовину по сравнению со сложным режимом . Это содержание следующей теоремы.
Теорема 1.3.
Предположим, что P⊆C2 выполняет восстановление фазы. Если A=diag(α,β)∈GL2(R) удовлетворяет условию |det(A)|−1≥2, то ({gp}p∈P,(0,β4)T+AZ2) выполняет восстановление фазы на L2(R ,Р).
Две приведенные выше теоремы включают в качестве предположения, что векторы p, определяющие используемые оконные функции, образуют семейство, выполняющее фазовый поиск в C2.
Общеизвестно, что сложно решить, выполняет ли данный кадр поиск фазы в Cn или нет [6, 19, 8, 23, 9] .
Что касается задачи восстановления фазы в C2, то известно, что верна так называемая гипотеза 4n−4, то есть в размерности n=2 никакое семейство из трех и менее векторов не восстанавливает фазу, а общее семейство из четырех ( или больше) векторов делает работу [6, теор. 10] .
Напомним, что m векторов φ1,…,φm∈Cn называются общими, если они принадлежат некоторому непустому открытому по Зарисскому подмножеству Cn×m≃(Rn×m)2.
В этой статье мы отменим предположение о том, что фрейм является общим, и установим следующую характеристику для системы из четырех векторов, чтобы выполнять фазовый поиск в C2. Эта характеристика дает нам сразу легко проверяемое геометрическое условие выбора четырех оконных функций для рассматриваемой задачи.
10] .
Напомним, что m векторов φ1,…,φm∈Cn называются общими, если они принадлежат некоторому непустому открытому по Зарисскому подмножеству Cn×m≃(Rn×m)2.
В этой статье мы отменим предположение о том, что фрейм является общим, и установим следующую характеристику для системы из четырех векторов, чтобы выполнять фазовый поиск в C2. Эта характеристика дает нам сразу легко проверяемое геометрическое условие выбора четырех оконных функций для рассматриваемой задачи.
Теорема 1.4.
Пусть φ0,φ1,φ2,φ3∈C2. Кроме того, определите
| λk:=⟨φk,φ0⟩,µk:=⟨φk,(0−110)¯¯¯¯¯¯φ0⟩,k∈{1,2,3}. |
Следующие операторы эквивалентны:
{φ0,φ1,φ2,φ3}⊆C2 выполняет поиск фазы.
Верно, что µk≠0, k∈{1,2,3} и что числа λ1/µ1,λ2/µ2,λ3/µ3 не коллинеарны.
Комбинируя теоремы 1.2, теоремы 1.3 и теоремы 1.4, мы приходим к следующему довольно явному результату.
Следствие 1.5.
Предположим, что λ1,λ2,λ3∈C не лежат на одной прямой, и определить
| П:={(10),(λ11),(λ21),(λ31)}. |
Если A∈GL2(R) удовлетворяет условию |det(A)|−1李4, то ({gp}p∈P,AZ2) выполняет поиск фазы на L2(R). Более того, если A=diag(α,β)∈GL2(R) удовлетворяет условию |det(A)|−1李2, то ({gp}p∈P,(0,β4)T+AZ2) выполняет фазовый поиск на L2 (Р, Р).
Рисунок 1. Графики действительной и мнимой частей четырех оконных функций gp1,…,gp4, подвергнутых точечной конфигурации P={p1,…,p4}⊆C2, заданной P={(10),(11),(− 11),(i1)}. Согласно следствию 1.5, ({gp}p∈P,AZ2) выполняет фазовый поиск на L2(R) при условии, что |det(A)|−1≥4.1.2. Терминология и обозначения
На протяжении всего изложения мы будем небрежно отождествлять R2 с комплексной плоскостью C в силу отображения (x,y)T↦x+iy. Для подмножества S⊆C обозначим через ¯¯¯¯S множество, состоящее из соответствующих комплексно-сопряженных чисел S, т. е. ¯¯¯¯S\coloneqq{s∈C:¯¯¯s∈S}. Аналогичным образом, если S⊆R2, то ¯¯¯¯S означает множество ¯¯¯¯S\coloneqq{(x,y)T∈R2:(x,−y)T∈S}.
е. ¯¯¯¯S\coloneqq{s∈C:¯¯¯s∈S}. Аналогичным образом, если S⊆R2, то ¯¯¯¯S означает множество ¯¯¯¯S\coloneqq{(x,y)T∈R2:(x,−y)T∈S}.
Для множества Ω и класса функций A⊆CΩ мы говорим, что Z⊆Ω есть множество единственности для A, если
| (f∈A: f|Z=0)⟹f≡0. |
Подмножество Λ⊆R2≃C называется сдвинутой решеткой, если существуют вектор v∈R2 и обратимая матрица A∈GL2(R) такие, что
| Λ=v+AZ2={v+Ax:x∈Z2}. |
Матрица A называется порождающей матрицей Λ. Сдвинутая решетка Λ называется сепарабельной, если она порождена диагональной матрицей. Для матрицы A∈C2×2 мы обозначаем через A∗ сопряженную транспонированную матрицу A, т. е. A∗=(¯¯¯¯A)T.
Как обычно, мы обозначаем через L2(R) пространство Лебега всех измеримых, комплекснозначных и суммируемых с квадратом функций f:R→C. Подпространство в L2(R), состоящее из всех вещественнозначных функций из L2(R), обозначается через L2(R,R). Кратковременное преобразование Фурье Vgf функции f∈L2(R) относительно оконной функции g∈L2(R) определяется как в уравнении (1). Это равномерно непрерывное отображение, удовлетворяющее соотношению ∥Vgf∥L2(R2)=∥f∥L2(R)∥g∥L2(R) [18, следствие 3.2.2] . Следовательно, f↦Vgf образует изометрию из L2(R) в L2(R2), если ∥g∥L2(R)=1.
Наконец, векторное пространство Cn,n∈N снабжено скалярным произведением ⟨v,w⟩=∑nj=1vj¯¯¯¯¯¯wj, где v=(v1,…,vn)T∈Cn и w= (w1,…,wn)T∈Cn.
Кратковременное преобразование Фурье Vgf функции f∈L2(R) относительно оконной функции g∈L2(R) определяется как в уравнении (1). Это равномерно непрерывное отображение, удовлетворяющее соотношению ∥Vgf∥L2(R2)=∥f∥L2(R)∥g∥L2(R) [18, следствие 3.2.2] . Следовательно, f↦Vgf образует изометрию из L2(R) в L2(R2), если ∥g∥L2(R)=1.
Наконец, векторное пространство Cn,n∈N снабжено скалярным произведением ⟨v,w⟩=∑nj=1vj¯¯¯¯¯¯wj, где v=(v1,…,vn)T∈Cn и w= (w1,…,wn)T∈Cn.
1.3. Контур
В разделе 2 мы собираем все предварительные результаты, касающиеся свойств пространств Фока, уделяя особое внимание множествам уникальности и выборкам, которые понадобятся на протяжении всей статьи. Раздел 3 посвящен доказательству полной характеризации векторов, выполняющих восстановление фазы в C2.
Основываясь на фундаменте, заложенном в Разделах 2 и 3, мы переходим к получению и использованию новой связи между фазовым поиском в конечной системе координат, наборами уникальности в пространствах Фока, а также бесфазной выборкой STFT. В частности, мы доказываем результаты бесфазной выборки, изложенные в разделе 1.1, включая несколько расширений для нерегулярной выборки.
В частности, мы доказываем результаты бесфазной выборки, изложенные в разделе 1.1, включая несколько расширений для нерегулярной выборки.
2. Предварительные на пространствах Фока
Этот раздел посвящен тому, чтобы напомнить и собрать несколько фактов о фоковских пространствах. За обширным изложением темы фоковских пространств мы отсылаем к учебнику Чжу [24] .
2.1. Основные свойства и отношения к STFT
Пространство L2α(C) состоит из всех измеримых по Лебегу функций F:C→C, для которых
| ∥F∥α\coloneqq(απ∫C|F(z)|2e−α|z|2dA(z))12<∞ |
где dA(z) обозначает евклидову меру площади на C. Если O(C) представляет собой совокупность всех целых функций на C, то пространство Фока (или пространство Баргмана-Фока) определяется как пересечение
| F2α(C)\coloneqqL2α(C)∩O(C). |
Точечная оценка
| (3) | |F(z)|e−α|z|2/2≤∥F∥α |
, который выполняется для каждого F∈F2α(C) и каждого z∈C, переводит F2α(C) в гильбертово пространство с воспроизводящим ядром (RKHS) со скалярным произведением
⟨F,G⟩α=απ∫CF(z)¯¯¯¯¯¯¯¯¯¯¯¯¯G(z)e−α|z|2dA(z). |
Кроме того, структура RKHS предполагает следующее утверждение.
Лемма 2.1.
Пусть α,β>0 и F∈F2α(C) и G∈F2β(C). Тогда верно, что FG∈F2α+β(C).
Доказательство.
Использование поточечной оценки, приведенной в уравнении (3), показывает, что
| ∥FG∥2α+β | =α+βπ∫C|F(z)G(z)|2e−(α+β)|z|2dA(z) | ||
| ≤α+βπ∥F∥2α∫C|G(z)|2e−β|z|2dA(z) | |||
| =α+ββ∥F∥2α∥G∥2β<∞, |
по желанию. ∎
Для данной функции F∈F2α(C) мы определяем (взвешенный) сдвиг F на a∈C как
| (4) | TaF(z)\coloneqqeαz¯¯¯a−α2|a|2F(z−a). |
Согласно [24, предложение 2.38] оператор Ta является унитарным оператором на F2α(C) для любого a∈C. Мы называем Ta:F2α(C)→F2α(C) оператором сдвига (по a∈C) на F2α(C).
Мы называем Ta:F2α(C)→F2α(C) оператором сдвига (по a∈C) на F2α(C).
Если f∈L2(R), то преобразование Баргмана Bf функции f, определяемое как
| Bf(z)\coloneqq21/4∫Rf(t)e2πtz−πz2−π2t2dt, |
удовлетворяет Bf∈O(C). Фактически преобразование Баргмана B является изоморфизмом между гильбертовыми пространствами L2(R) и F2π(C) [24, теорема 6.8] . Существует тесная связь между STFT с окнами Эрмита и преобразованием Баргмана с точки зрения полианалитических функций, см., например, [1, раздел 3] . Для наших целей большое значение будут иметь два тождества: с
| (5) | η(z):=exp(−πixy+π2|z|2),z=x+iy∈C, |
для всех f∈L2(R) и для всех z=x+iy выполняется
| (6) | Vh0f(x,−y)⋅η(z) | = Бф(г), | ||
| (7) | Vh2f(x,−y)⋅η(z) | =(Bf)′(z)−π¯zBf(z). |
2.2. Наборы уникальности и выборки
Напомним, что множество Z⊆C является множеством единственности для F2α(C), если каждая функция из F2α(C), обращающаяся в нуль на Z, должна тождественно обращаться в нуль. Если Z={zn:n∈N} — последовательность различных точек в C, то Z называется набором дискретизации для F2α(C), если существует константа C>0 такая, что
| C−1∥F∥2α≤∞∑n=1|F(zn)|2e−α|zn|2≤C∥F∥2α |
для всех F∈F2α(C). Ясно, что каждый набор выборки является набором уникальности. Далее, мы говорим, что Z⊆C раздельно (или: равномерно дискретно), если
| infz,z′∈Zz≠z′|z−z′|>0. |
Обозначив через Br(w)\coloneqq{z∈C:|z−w|
D−(Z)\coloneqqliminfr→∞(infw∈C#(Z∩Br(w))πr2). |
Например, если Z=AZ2,A∈GL2(R) является решеткой, то D−(Z)=|det(A)|−1. Среди решеток множества единственности характеризуются своей плотностью.
Теорема 2.2 (Переломов
[21] ).Решетка AZ2⊆C,A∈GL2(R) является множеством единственности для F2α(C) тогда и только тогда, когда |det(A)|−1≥α/π.
Для общих разделенных множеств мы имеем следующую характеристику множеств выборки.
Теорема 2.3 (Любарский
[20] , Сейп и Вальстен [22] ).Если Z⊆C разделен, то Z является набором дискретизации для F2α(C) тогда и только тогда, когда D−(Z)>α/π.
С помощью оператора сдвига, определенного в уравнении (4), мы можем легко проверить, что свойство множества Z⊆C быть множеством единственности для F2α(C) инвариантно относительно переносов. Действительно, если Z — множество единственности и если v∈C, то функция F∈F2α(C) обращается в нуль в точке v+Z={v+z:z∈Z} тогда и только тогда, когда T−vF∈F2α(C) обращается в нуль в Z. Следовательно, T−vF≡0 и тот факт, что T−vF равно F(⋅+v) с точностью до ненулевого весового коэффициента, заставляет F тождественно обращаться в нуль.
Следовательно, T−vF≡0 и тот факт, что T−vF равно F(⋅+v) с точностью до ненулевого весового коэффициента, заставляет F тождественно обращаться в нуль.
Обратите внимание, что в отличие от выборочных множеств общая характеристика множеств единственности в F2α(C) с точки зрения плотности представляет собой сложную задачу, а множества единственности могут иметь неожиданную структуру. Например, Асенси, Любарский и Сейп показали, что если
| R\coloneqq{(1,0),(−1,0)}∪{(±√2n,0):n∈N}∪{(0,±√2n):n∈N} |
, то √π/αR — множество единственности для F2α(C), обладающее тем свойством, что существуют сколь угодно большие диски, не содержащие точек из √π/αR [4] . В частности, верно, что D−(R)=0. Наконец, упомянем необходимое условие плотности, полученное Беловым, Боричевым и Кузнецовым, которые доказали в [7] , что если Z⊆C есть множество единственности для F2π(C), то
limsupr→∞#(Z∩Br(0))πr2≥13π. |
3. Фазовый поиск в C2
Цель настоящего раздела состоит в том, чтобы дать полную характеристику извлечения фазы в C2. Именно, докажем следующее утверждение.
Теорема 3.1.
Пусть φ0,φ1,φ2,φ3∈C2. Кроме того, определите
| λk:=⟨φk,φ0⟩,µk:=⟨φk,(0−110)¯¯¯¯¯¯φ0⟩,k∈{1,2,3}. |
Следующие операторы эквивалентны:
{φ0,φ1,φ2,φ3}⊆C2 выполняет поиск фазы.
Верно, что µk≠0, k∈{1,2,3} и что числа λ1/µ1,λ2/µ2,λ3/µ3 не коллинеарны.
3.1. Вспомогательные результаты
Прежде чем перейти к доказательству теоремы 3.1, приведем несколько важных фактов. Во-первых, мы требуем, чтобы свойство восстановления фазы было инвариантным относительно обратимых линейных преобразований.
Лемма 3.2.
Пусть Φ={φk}k∈I⊆Cn и A∈GLn(C). Тогда Φ выполняет фазовый поиск в Cn тогда и только тогда, когда ~Φ:={Aφk}k∈I выполняет фазовый поиск в Cn.
Доказательство.
Очевидно, поскольку можно заменить Φ на ~Φ и A на A−1 соответственно, достаточно показать одно следствие.
Предположим, что Φ выполняет восстановление фазы, и предположим, что
z,z′∈Cn таковы, что
| (8) | |⟨z,Aφk⟩|=|⟨z′,Aφk⟩|, ∀k∈I. |
Нам нужно показать, что z~z′. Из (8) следует, что
| |⟨A∗z,φk⟩|=|⟨A∗z′,φk⟩|,∀k∈I. |
Поскольку Φ выполняет восстановление фазы, это означает, что A∗z∼A∗z′. Поскольку A∗ обратим, мы получаем, что z∼z′, и готово. ∎
Кроме того, центральную роль будет играть следующее геометрическое условие, гарантирующее, что точка на плоскости однозначно определяется своим расстоянием от трех фиксированных точек.
Лемма 3.3.
Пусть z,w,a1,a2,a3∈C такие, что
| (9) | |z−aj|=|w−aj|,j∈{1,2,3}. |
Если a1,a2,a3 не коллинеарны, то z=w. Наоборот, если a1,a2,a3 коллинеарны, существуют z≠w такие, что (9) держит.
Доказательство.
Предположим противное, что z≠w. Тогда существует единственный отрезок L конечной длины, соединяющий точки z и w. Предположение, что |z−aj|=|w−aj| для всех j∈{1,2,3} следует, что a1,a2,a3 лежат на единственном серединном перпендикуляре к отрезку L. Это противоречит предположению, что a1,a2,a3 не лежат на одной прямой.
Для второго утверждения пусть J обозначает прямую, содержащую три точки a1,a2,a3. Поскольку точки лежат на одной прямой, такая прямая существует.
Пусть z — любая точка в C∖J, а w — отражение z через J. Тогда z≠w удовлетворяет (9).
∎
Теперь мы хорошо подготовлены для работы со следующей простой конфигурацией.
Предложение 3.4.
Пусть β1,β2,β3∈C. Семья
| {(10),(β11),(β21),(β31)}⊆C2 |
выполняет поиск фазы тогда и только тогда, когда β1,β2,β3 не коллинеарны.
Доказательство.
Положим φ0:=(1,0)T и φk:=(βk,1)T, k∈{1,2,3}. Мы действуем в два этапа и показываем
- .
Если β1,β2,β3 не коллинеарны, то {φk}3k=0 выполняет поиск фазы.
Если β1,β2,β3 коллинеарны, то {φk}3k=0 не выполняет восстановление фазы.
Этап а) Предположим, что β1,β2,β3 не коллинеарны, и пусть z,w∈C2 с z=(z1,z2)T и w=(w1,w2)T таковы, что
| (10) | |⟨z,φk⟩|=|⟨w,φk⟩|,k∈{0,1,2,3}. |
Нам нужно доказать, что z∼w.
Для этого мы различаем два случая в зависимости от z1=0 или z1≠0.
Если z1=0, то
| |w1|=|⟨w,φ0⟩|=|⟨z,φ0⟩|=0, |
и
| |w2|=|⟨w,φ1⟩|=|⟨z,φ1⟩|=|z2|. |
Таким образом, в данном случае имеем z∼w. Если z1≠0, мы получаем, что
| (11) | |w1|2=|⟨w,φ0⟩|2=|⟨z,φ0,⟩|2=|z1|2≠0. |
Кроме того, по предположению имеем, что
| |¯βkz1+z2|=|¯βkw1+w2|,k∈{1,2,3}. |
Деление на |z1|=|w1|≠0 означает, что
| ∣∣∣z2z1+¯¯¯¯¯βk∣∣∣=∣∣∣w2w1+¯¯¯¯¯βk∣∣∣,k∈{1,2,3}. |
Заметим, что −¯β1,−¯β2,−¯β3 не коллинеарны, так как β1,β2,β3 не коллинеарны. Таким образом, применение леммы 3.3 дает, что z2/z1=w2/w1, что эквивалентно
| z2w1z1=w2. |
Следовательно, при τ:=w1/z1∈T мы действительно имеем τz=w. В частности, отсюда следует, что z∼w.
Шаг b) Предположим теперь, что β1,β2,β3 коллинеарны.
Нам нужно найти пару векторов z,w∈C2, которые не эквивалентны при выполнении (10).
Согласно лемме 3.3 существуют комплексные числа p≠q такие, что |p−βk|=|q−βk| для каждого k∈{1,2,3}.
Так как p≠q мы имеем
| z=(−1¯p),w=(−1¯q) |
не эквивалентны. Кроме того, верно, что |⟨z,φ0⟩|=1=|⟨w,φ0⟩|, и для каждого k∈{1,2,3}
Кроме того, верно, что |⟨z,φ0⟩|=1=|⟨w,φ0⟩|, и для каждого k∈{1,2,3}
| |⟨z,φk⟩|=|p−βk|=|q−βk|=|⟨w,φk⟩|, |
что подтверждает доказательство. ∎
3.2. Доказательство теоремы 3.1.
Идея доказательства состоит в том, чтобы свести общую ситуацию к довольно частной конфигурации в предложении 3.4.
Сначала заметим, что если φ0=0, семейство {φk}3k=0 не может выполнять фазовый поиск. В самом деле, предположим, что он выполняет поиск фазы, тогда также {φk}3k=1 выполняет поиск фазы. Это приводит к противоречию, так как известно, что семейство векторов в C2, выполняющее фазовый поиск, состоит как минимум из четырех элементов [6, теор. 10] .
Таким образом, мы можем предположить, что φ0=(p,q)T≠0, и определить
| A:=(¯p¯q−qp)∈GL2(C). |
У нас есть это
| Aφ0=(|p|2+|q|20), |
и для каждого k∈{1,2,3}
Применение леммы 3. 2 дает, что {φk}3k=0 выполняет фазовый поиск тогда и только тогда, когда
2 дает, что {φk}3k=0 выполняет фазовый поиск тогда и только тогда, когда
| ~Φ:={(|p|2+|q|20),(λ1µ1),(λ2µ2),(λ2µ2)} |
выполняет поиск фазы.
Остается показать, что функция ~Φ выполняет восстановление фазы тогда и только тогда, когда выполняется условие ii).
Мы начнем с первой импликации и предположим, что ~Φ выполняет восстановление фазы. Отсюда следует, что µk≠0 при k∈{1,2,3}; действительно, если бы мы имели, что µk=0 для некоторого k, это означало бы, что существует пара линейно зависимых векторов в ~Φ. Тогда мы могли бы свести ~Φ к семейству трех векторов, которое выполняет восстановление фазы в C2, и снова получить противоречие.
Поскольку свойство восстановления фазы инвариантно относительно умножения на ненулевой скаляр отдельных векторов, мы получаем, что также
| Ψ:={(10),(λ1/µ11),(λ2/µ21),(λ3/µ31)} |
выполняет поиск фазы. Привлечение предложения 3.4 дает тогда, что точки
Привлечение предложения 3.4 дает тогда, что точки
| λ1/μ1, λ2/μ2, λ3/μ3 |
не коллинеарны.
Для второго следствия предположим ii).
Согласно предложению 3.4 мы имеем, что Ψ выполняет поиск фазы. Умножая каждый из отдельных векторов на соответствующие ненулевые скаляры, мы получаем, что ~Φ действительно выполняет восстановление фазы, и завершаем доказательство.
4. Выборка спектрограммы
Этот раздел объединяет результаты, представленные в Разделах 2 и 3, и устанавливает новый подход к получению результатов бесфазной выборки для задачи восстановления фазы STFT. Начав с абстрактного результата о бесфазовой выборке для общих классов сигналов C⊆L2(R), мы перейдем к изучению случая, когда пространством сигналов является все пространство L2(R), после чего следует рассмотрение класса сигналов C=L2(R). Р, Р).
4.1. Бесфазовый отбор проб
Мы начинаем с создания несколько абстрактного результата поиска фазы, чтобы выделить, какие ингредиенты необходимы для наших результатов.
Предложение 4.1.
Предположим, что P⊆C2 выполняет восстановление фазы. Более того, пусть C⊆L2(R) — сигнальный класс, и пусть Λ⊆R2 таково, что ¯Λ набор уникальности для
| (12) | A(C):={Bf: f∈C}∪{BfBh((Bf)′Bh−(Bh)′Bf): f,h∈C}. |
Тогда верно, что ({gp}p∈P,Λ) выполняет восстановление фазы на C.
Доказательство.
Предположим, что f,h∈C таковы, что для всех z∈Λ выполняется
| (13) | |Vgpf(z)|=|Vgph(z)|,p∈P. |
Нам нужно показать, что f∼h. Доказательство состоит из двух основных шагов: Сначала рассмотрим задачу фазового поиска локального аромата и покажем, что для каждой точки z∈Λ выполняется
| (14) | (Vh0f(z)Vh2f(z))∼(Vh0h(z)Vh2h(z)). |
Второй шаг состоит в объединении локальной информации, полученной на первом шаге, с использованием предполагаемых свойств множества Λ, чтобы сделать вывод, что f∼h.
Шаг 1:
Для любых z∈Λ, f∈L2(R) и p=(λ,µ)∈C2 имеем
| |Vgpf(z)|=∣∣¯λVh0f(z)+¯µVh2f(z)∣∣=∣∣∣⟨(Vh0f(z)Vh2f(z)),p⟩∣∣∣. |
Так как P выполняет поиск фазы, это следует из
(13) что эквивалентность
(14) верно для всех z∈Λ.
Шаг 2:
Обозначим через F,H преобразования Баргмана функций f и h соответственно.
Используя тождества (6) и (7), легко видеть, что из (14) для всех z∈Λ следует, что
| (15) | (F(z)F′(z))∼(H(z)H′(z)),∀z∈¯Λ |
Таким образом, имеем
| |F|2|¯Λ=|H|2|¯Λand(¯¯¯¯FF′)|¯Λ=(¯¯¯¯¯HH′)|¯Λ. |
Основная идея состоит в хитром сочетании этих двух тождеств, а именно в том, чтобы сделать наблюдение, что
| |F|2⋅¯¯¯¯¯¯HH′−|H|2⋅¯¯¯¯FF′=¯¯¯¯¯¯¯¯¯FH(FH′−F′H) |
обращается в нуль на ¯Λ. Таким образом, также
G:=FH(FH′−F′H) обращается в нуль на ¯Λ. Поскольку G∈A(C), из предположения на Λ следует, что G обращается в нуль всюду на C.
Таким образом, поскольку произведение G состоит из множителей F,H,FH′−F′H, являющихся целыми функциями, по крайней мере один из них должен быть нулевой функцией.
Таким образом, также
G:=FH(FH′−F′H) обращается в нуль на ¯Λ. Поскольку G∈A(C), из предположения на Λ следует, что G обращается в нуль всюду на C.
Таким образом, поскольку произведение G состоит из множителей F,H,FH′−F′H, являющихся целыми функциями, по крайней мере один из них должен быть нулевой функцией.
Если F=0, то из (15) следует, что H обращается в нуль на ¯Λ. Поскольку H∈A(C), отсюда следует, что и H тождественно обращается в нуль. Следовательно, мы имеем, что f=h=0 и, в частности, f∼h.
Таким же образом доказывается, что f ∼h в случае, когда H тождественно обращается в нуль.
Чтобы закончить доказательство, осталось рассмотреть случай, когда ни F, ни H не равны нулю тождественно и когда FH′−F′H=0.
Пусть E⊆C — область, в которой F не имеет нулей, тогда для всех z∈E имеем
| (H/F)'(z)=(FH’-F’H)(z)F2(z)=0. |
Следовательно, H=cF на E для подходящей константы c∈C. По аналитичности получаем, что H=cF на C.
Кроме того, поскольку |H|=|F| на ¯Λ для всех z∈¯Λ имеем
| |F(z)|=|H(z)|=|cF(z)|, |
откуда следует, что (1−|c|)F обращается в нуль на ¯Λ. По условию F∈A(C)∖{0} и, следовательно, не может обращаться в нуль на всех ¯Λ. Отсюда заключаем, что |c|=1. Поскольку преобразование Баргмана инъективно, из
| следует | B(h-cf)=H-cF=0 |
что действительно h∼f. ∎
Роль множества Λ в предложении 4.1 на данном этапе еще несколько скрыта. Однако примечательно, что A(C) состоит только из целых функций. Таким образом, мы свели проблему нахождения конфигурации, выполняющей фазовый поиск, к проблеме идентификации множеств уникальности для подклассов O(C). На самом деле об A(C) можно сказать даже больше.
Лемма 4.2.
Для всех C⊆L2(R) выполняется A(C)⊆F24π(C).
Доказательство.
Прежде всего заметим, что для всех f∈L2(R) верно Bf∈F2π(C)⊆F24π(C). Остается показать, что для всех f,h∈L2(R) выполняется
Остается показать, что для всех f,h∈L2(R) выполняется
| (16) | (Bf)′Bh−Bf(Bh)′∈F22π(C). |
В самом деле, из (16) следует дважды применить лемму 2.1, что
| BfBh[(Bf)′Bh−Bf(Bh)′]∈F24π(C), |
и готово. Для доказательства (16) используем тождество (7) для выражения производных преобразований Баргмана по формуле
| (Бф)'(з) | =Vh2f(¯z)η(z)+π¯zBf(z), | ||
| (Бх)'(з) | =Vh2h(¯z)η(z)+π¯zBh(z). |
Таким образом, мы получаем, что
| [(Bf)′Bh−Bf(Bh)′](z)=[Vh2f(¯z)η(z)+π¯zBf(z)]Bh(z)−Bf(z)[Vh2h(¯z )η(z)+π¯zBh(z)] |
Так как два члена, содержащие ¯z как множитель, сокращаются, мы получаем, что
| (17) | [(Bf)′Bh−Bf(Bh)′](z)=η(z)[Vh2f(¯z)Bh(z)−Bf(z)Vh2h(¯z)]. |
Для первого члена в правой части мы получаем, что
| ∥η(z)Vh2f(x,−y)Bh(z)∥22π | =2∫Ceπ|z|2|Vh2f(¯z)|2|Bh(z)|2e−2π|z|2dA(z) | ||
| ≤2∥Vh2f∥2L2(C)∥(Bh)e−π|⋅|2/2∥2L∞(C) | |||
| ≤2∥f∥2L2(R)∥Bh∥2π | |||
| =2∥f∥2L2(R)∥h∥2L2(R) | |||
| <∞, |
, где мы использовали поточечную оценку, приведенную в уравнении (3).
Поскольку со вторым слагаемым в правой части (17) можно поступить таким же образом, мы приходим к желаемому выводу.
∎
Лемма 4.2 позволяет применить теоремы 2.3 и теоремы 2.2, и мы получаем следующий результат как прямое следствие предложения 4.1.
Теорема 4.3.
Предположим, что P⊆C2 выполняет восстановление фазы. Кроме того, пусть Λ ⊆ R2 отделяется с D−(Λ)>4.
Тогда верно, что ({gp}p∈P,Λ) выполняет фазовый поиск на L2(R).
Более того, если Λ — сдвинутая решетка, то достаточно, чтобы D−(Λ)≥4 выполнялось утверждение.
Кроме того, пусть Λ ⊆ R2 отделяется с D−(Λ)>4.
Тогда верно, что ({gp}p∈P,Λ) выполняет фазовый поиск на L2(R).
Более того, если Λ — сдвинутая решетка, то достаточно, чтобы D−(Λ)≥4 выполнялось утверждение.
4.2. Бесфазовая выборка в L2(R,R)
Рассмотрим включение пространств Фока F2α(C)⊆F2β(C) при 0<α<β вместе с характеристикой множеств единственности среди решеток и множеств выборок, приведенных в теоремах 2.2 и теоремах 2.3 соответственно. Включение и характеристика формально подтверждают интуитивное предположение о том, что с ростом пространства выборки F2α(C) растет и информация о выборках Z⊆C, необходимая для однозначного восстановления любой функции из F2α(C) посредством выборки на Z. Предоставленная информация образцами напрямую связано с их более низкой плотностью Берлинга D−(Z). Это послужило первоначальным толчком к исследованию задач бесфазовой выборки для классов функций C, являющихся собственными подпространствами в L2(R). Интуитивно мы ожидаем, что ограничение задачи восстановления фазы STFT подпространством C⊆L2(R) приводит к результатам бесфазовой выборки с уменьшенной плотностью. Мы уделяем особое внимание важному классу C=L2(R,R) вещественнозначных функций, что является естественным предположением, которое делается в различных приложениях. Цель настоящего раздела состоит в том, чтобы показать, что плотность, достаточная для восстановления реальных сигналов от бесфазных отсчетов, может быть уменьшена в два раза по сравнению с достаточной плотностью в комплексном режиме. Начнем с леммы о преобразовании Баргмана действительнозначного отображения.
Мы уделяем особое внимание важному классу C=L2(R,R) вещественнозначных функций, что является естественным предположением, которое делается в различных приложениях. Цель настоящего раздела состоит в том, чтобы показать, что плотность, достаточная для восстановления реальных сигналов от бесфазных отсчетов, может быть уменьшена в два раза по сравнению с достаточной плотностью в комплексном режиме. Начнем с леммы о преобразовании Баргмана действительнозначного отображения.
Лемма 4.4.
Предположим, что функция f∈L2(R,R) является вещественной. Тогда для каждого z∈C и каждого n∈N0 верно, что
| ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(Bf)(n)(z)=(Bf)(n)(¯¯¯z). |
Доказательство.
Из определения преобразования Баргмана следует, что если f∈L2(R,R), то Bf является вещественнозначным на вещественной оси. Как следствие, также (Bf)(n) является вещественным на действительной оси для каждого n∈N0. Следовательно, для каждого z∈R и каждого n∈N0 имеем
(Bf)(n)(z)=¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(Bf)(n)(¯¯¯z). Заметьте, что правая часть предыдущего тождества продолжается от z∈R до целой функции. Таким образом, утверждение является следствием теоремы тождества.
∎
Заметьте, что правая часть предыдущего тождества продолжается от z∈R до целой функции. Таким образом, утверждение является следствием теоремы тождества.
∎
В качестве применения леммы 4.4 следующий результат показывает, что подходящая декомпозиция множества единственности для A(L2(R)) приводит к редукции множеств единственности для A(L2(R,R)).
Лемма 4.5.
Пусть Λ⊆C и существует подмножество Γ⊆Λ такое, что
| Λ=Γ∪¯¯¯¯Γ. |
Если Λ — множество единственности для класса A(L2(R)), то Γ — множество единственности для класса A(L2(R,R)).
Доказательство.
Пусть f,h∈L2(R,R) — две вещественнозначные функции. Далее, пусть F=Bf и H=Bh — преобразование Баргмана функций f и h соответственно. Кроме того, определите G=FH(FH′−F′H). Нам нужно показать, что если F|Γ=0, то F≡0, а если G|Γ=0, то G≡0. Из леммы 4.4 мы знаем, что ¯¯¯¯¯¯¯¯¯¯¯F(z)=F(¯¯¯z) и ¯z) для любого z∈C. Следовательно, если F обращается в нуль в точке γ∈Γ, то F обращается в нуль в точке ¯¯¯γ∈¯¯¯¯Γ, и то же свойство выполняется для функции G. Это показывает, что и F, и G обращаются в нуль в точке Γ∪¯¯¯¯Γ= Λ. Но Λ является множеством единственности для класса A(L2(R))⊇A(L2(R,R)). Следовательно, F=0 и G=0, что дает утверждение.
∎
Это показывает, что и F, и G обращаются в нуль в точке Γ∪¯¯¯¯Γ= Λ. Но Λ является множеством единственности для класса A(L2(R))⊇A(L2(R,R)). Следовательно, F=0 и G=0, что дает утверждение.
∎
Аналогично тому, как в разделе 4.1, мы получаем следующий абстрактный результат единственности для класса сигналов C=L2(R,R), который следует непосредственно из леммы 4.5 и предложения 4.1.
Предложение 4.6.
Предположим, что P⊆C2 выполняет восстановление фазы. Кроме того, предположим, что Λ⊆C обладает тем свойством, что ¯¯¯¯Λ является множеством единственности для класса A(L2(R)). Далее, предположим, что Γ⊆Λ удовлетворяет условию Λ=Γ∪¯¯¯¯Γ. Тогда верно, что ({gp}p∈P,Γ) выполняет фазовый поиск на L2(R,R).
Например, в ситуации предложения 4.6 мы замечаем, что если Λ — множество единственности для класса A(L2(R)), симметричное относительно вещественной оси, т. е. Λ=¯¯¯¯Λ, тогда ({gp}p∈P,Λ∩H+) выполняет фазовый поиск на A(L2(R,R)), где H+\coloneqq{z∈C:Im(z)≥0} обозначает закрытая верхняя полуплоскость. Фактически восстановление фазы на A(L2(R,R)) возможно из сдвинутых решеток Λ⊆R2 с плотностью D−(Λ)≥2, т.е. по сравнению со сложным случаем достижимо уменьшение плотности вдвое.
Фактически восстановление фазы на A(L2(R,R)) возможно из сдвинутых решеток Λ⊆R2 с плотностью D−(Λ)≥2, т.е. по сравнению со сложным случаем достижимо уменьшение плотности вдвое.
Теорема 4.7.
Предположим, что P⊆C2 выполняет восстановление фазы. Кроме того, пусть Λ=αZ×βZ с α,β∈R∖{0} — сепарабельная решетка плотности D−(Λ)≥2. Тогда верно, что ({gp}p∈P,(0,β4)T+Λ) выполняет фазовый поиск на L2(R,R).
Доказательство предыдущего утверждения основано на следующей лемме.
Лемма 4.8.
Предположим, что Λ⊆R2 — сдвинутая решетка вида Λ=(0,β2)T+(αZ+βZ) с α,β∈R∖{0}. Далее определим сдвинутые решетки Γ1,Γ2⊆R2 через
| Γ1=(0β2)+(α002β)Z2, Γ2=(0β2)+(α0β2β)Z2 |
Тогда верно следующее:
Γ1 и Γ2 — смещенные подрешетки Λ
Справедливо, что D−(Λ)=(αβ)−1 и что D−(Γ1)=D−(Γ2)=(2αβ)−1
Λ=Γ1∪¯¯¯¯¯¯Γ1=Γ2∪¯¯¯¯¯¯Γ2.
Доказательство.

Используя критерий того, что решетка AZ2 является подрешеткой BZ2 при условии, что B−1A∈GL2(Z), показывает, что Γ1 и Γ2 являются сдвинутыми подрешетками Λ. Второе утверждение непосредственно следует из того, что для любой сдвинутой решетки v+AZ2,A∈GL2(R),v∈R2 выполняется равенство D−(v+AZ2)=|det(A)|−1. Осталось доказать третье утверждение. Начнем с того, что покажем включение Λ⊆Γ1∪¯¯¯¯¯¯¯Γ1. Для этого выберем произвольное z∈Λ. Тогда существует (n,k)T∈Z2 такое, что
| (18) | z=(αnβ(k+12)). |
Если k четно, то k=2m для некоторого m∈Z, что дает
| z=(0β2)+(α002β)(нм)∈Γ1. |
С другой стороны, если k нечетно, то k=2m−1 для некоторого m∈Z, что дает
z=(αnβ2+β(2m−1))=(αn−β2−2β(−m))=¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(0β2)+(α002β)( n−m)∈¯¯¯¯¯¯Γ1. |
В результате включение Λ⊆Γ1∪¯¯¯¯¯¯Γ1 верно, и нам осталось доказать, что ¯¯¯¯¯¯¯Γ1⊆Λ. Это, однако, является следствием того, что для каждого (n,k)T∈Z2 имеем
| № | ¯¯¯¯¯¯¯¯¯¯¯(0β2)+(α002β)(nk)=(αn−β2−2βk)=(0β2)+(α00β)(n1−2(k+1))∈Λ. |
В оставшейся части доказательства установим равенство Λ=Γ2∪¯¯¯¯¯¯Γ2. Таким же образом, как и выше, мы выбираем точку z∈Λ и замечаем, что z задается как в уравнении (18) для некоторого (n,k)T∈Z2. Если либо оба n,k четные, либо оба n,k нечетные, то k−n — четное целое число и существует m∈Z такое, что k−n=2m, или, что то же самое,
| k+12=n+2m+12. |
Это показывает, что точка z, определенная в (18), удовлетворяет соотношению
| z=(αnβ(n+2m+12))=(0β2)+(α0β2β)(nm)∈Γ2. |
С другой стороны, если n,k таковы, что одно из них четное, а другое нечетное, то k+n — нечетное число. Таким образом, существует m∈Z такое, что k+n+1=−2m, или, что то же самое,
Таким образом, существует m∈Z такое, что k+n+1=−2m, или, что то же самое,
| к+12=-(п+2м+12), |
что дает
| z=(αn−β(n+2m+12))=¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ ¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(0β2)+(α0β2β)(nm)∈¯¯¯¯¯¯¯Γ2. |
Таким образом, мы доказали, что Λ⊆Γ2∪¯¯¯¯¯¯Γ2. Чтобы доказать требуемое равенство, осталось показать, что ¯¯¯¯¯¯Γ2 ⊆ Λ. Но из этого легко следует, выбрав произвольное (n,k)T∈Z2 и заметив, что
| № | ¯¯¯¯¯¯¯¯¯¯¯¯(0β2)+(α0β2β)(nk)=(αn−β2−βn−2βk)=(0β2)+(α00β)(n−n−2k−1)∈Λ . |
∎
Доказательство Thm. 4.7.
Заметим, что сдвинутая решетка Γ\coloneqq(0,β4)T+Λ, указанная в формулировке теоремы, равна решетке Γ1, заданной в лемме 4.8, с заменой β на β2. Кроме того, лемма 4.8(iii) показывает, что
Γ∪¯¯¯¯Γ=(0,β4)T+(αZ×β2Z). |
Так как по условию D−(Λ)=(αβ)−1≥2, то сдвинутая решетка Γ∪¯¯¯¯Γ удовлетворяет условию D−(Γ∪¯¯¯¯Γ)=2 (αβ)−1≥4. В частности, Γ∪¯¯¯¯Γ является множеством единственности для A(L2(R)). Предложение 4.6 дает утверждение. ∎
Обратите внимание, что лемма 4.8 дает две возможности сдвинутых решеток, которые гарантируют восстановление фазы в L2(R,R), а именно Γ1 и Γ2. Сдвинутая решетка Γ1 сепарабельна, а Γ2 возникает из решетки вида aZ2,a>0 посредством поворота и последующего переноса. На рис. 2 изображена решетка Γ2.
Рис. 2. Сдвинутая решетка Γ и ее комплексно-сопряженная ¯¯¯¯Γ. Объединение Γ∪¯¯¯¯Γ представляет собой сдвинутую прямоугольную решетку Λ=(0,1/4)+12Z2 с D−(Λ)=4. В ситуации теоремы 4.3 ({gp},Λ) осуществляет восстановление фазы на L2(R), тогда как ({gp},Γ) выполняет восстановление фазы на L2(R,R).Благодарности
Мартин Ратмайр был поддержан Программой Эрвина-Шредингера (J-4523) Австрийский научный фонд (FWF).
Каталожные номера
- [1]
Абреу, Л.
 Д., и Файхтингер, Х. Г.
Функциональные пространства полианалитических функций.
В Гармоническом и комплексном анализе и его приложениях Тенденции
Мат. Биркхойзер/Спрингер, Чам, 2014 г., стр. 1–38.
Д., и Файхтингер, Х. Г.
Функциональные пространства полианалитических функций.
В Гармоническом и комплексном анализе и его приложениях Тенденции
Мат. Биркхойзер/Спрингер, Чам, 2014 г., стр. 1–38. - [2] Алайфари Р., Добеши И., Грохс П. и Инь Р. Поиск стабильной фазы в бесконечных измерениях. Найденный. вычисл. Мат. 19, 4 (август 2019 г.), 869–900.
- [3] Алайфари Р. и Веллерсхофф М. Восстановление фазы из дискретных величин преобразования Габора: Контрпримеры. Ж. Анал Фурье. заявл. 28, 1 (декабрь 2021 г.), 9.
- [4] Асенси Г., Любарский Ю., Сейп К. Распределение разложений Габора в фазовом пространстве. заявл. вычисл. Хармон. Анальный. 26, 2 (2009), 277–282.
- [5] Балан Р., Кристенсен Дж. Г., Криштал И. А., Окуджоу К. А. и Ромеро, Дж. Л. Многооконные рамы Gabor в амальгамных пространствах. Мат. Рез. лат. 21, 1 (2014), 55–69.
- [6] Бандейра А. С., Кэхилл Дж., Миксон Д. Г. и Нельсон А. А.
Сохранение фазы: приемистость и стабильность для восстановления фазы.
 заявл. вычисл. Хармон. Анальный. 37, 1 (2014), 106–125.
заявл. вычисл. Хармон. Анальный. 37, 1 (2014), 106–125. - [7] Белов Ю., Боричев А., Кузнецов А. Верхняя и нижняя плотности гауссовых систем Габора. заявл. вычисл. Хармон. Анальный. 49, 2 (2020), 438–450.
- [8] Бендори Т., Эдидин Д. Алгебраическая теория фазового поиска. arXiv: 2203.02774 (2022).
- [9] Бодманн, Б. Г., и Хаммен, Н. Стабильный поиск фазы с кадрами с низкой избыточностью. Доп. вычисл. Мат. 41, 2 (апрель 2015 г.), 317–331.
- [10] Грёхениг К., Ромеро Дж. Л. и Штёклер Дж. Точные результаты по выборке с производными в сдвиг-инвариантных пространствах и многооконные рамы Gabor. Констр. прибл. 51, 1 (2020), 1–25.
- [11] Грохс, П., и Лиер, Л. Инъективность восстановления фазы Габора из измерений решетки. архив: 2008.07238 (2020).
- [12] Грохс, П., и Лиер, Л. Теория неединственности в выборочном поиске фазы STFT. arXiv: 2207.05628 (2022).
- [13]
Грохс, П., и Лиер, Л.
Об основных барьерах дискретизации при поиске фазы STFT.
 Ж. Анал Фурье. заявл. 28, 39 (2022).
Ж. Анал Фурье. заявл. 28, 39 (2022). - [14] Грохс, П., и Лиер, Л. Стабильное восстановление фазы Габора в гауссовских инвариантных к сдвигу пространствах с помощью биортогональность. появиться в: Constr. прибл. (2022).
- [15] Грохс, П., и Ратмайр, М. Стабильный поиск фазы Габора и спектральная кластеризация. Комм. Чистое приложение Мат. 72, 5 (2019), 981–1043.
- [16] Грохс, П., и Ратмайр, М. Анализ L2-стабильности для восстановления фазы Габора. архив: 2108.06154 (2021).
- [17] Грохс, П., и Ратмайр, М. Стабильный поиск фазы Габора для многомерных функций. Дж. Евр. Мат. соц. 24, 5 (2022), 1593–1615.
- [18] Грёхениг, К. Основы частотно-временного анализа. Биркхойзер Базель, 2001.
- [19] Хейносаари Т., Мацарелла Л. и Вольф М. М. Квантовая томография в условиях априорной информации. Комм. Мат. физ. 318, 2 (март 2013 г.), 355–374.
- [20] Любарский, Ю.И.
Фреймы в пространстве Баргмана целых функций.
В Целых и субгармонических функциях, том.
 11 Доп.
Советская математика. амер. Мат. Soc., Провиденс, Род-Айленд, 1992, стр. 167–180.
11 Доп.
Советская математика. амер. Мат. Soc., Провиденс, Род-Айленд, 1992, стр. 167–180. - [21] Переломов, А. М. О полноте системы когерентных состояний. Теор. и математика. физ. 6 (1971), 156–164.
- [22] Сейп, К., и Вальстен, Р. Теоремы плотности для дискретизации и интерполяции в модели Баргмана-Фока пространство 2. Дж. Рейн Ангью. Мат. 429 (1992), 107–114.
- [23] Винсант, С. Небольшой кадр и сертификат его инъективности. 2015 Международная конференция по теории выборки и Приложения (СампТА) (2015), 197–200.
- [24] Чжу, К. Анализ пространств Фока, т. 1, с. 263 текста для выпускников в Математика. Спрингер, Нью-Йорк, 2012 г.
Использовать решетку в предложении
решетка
Реклама
- 332633
Advertisement
Advertisement
Advertisement
Advertisement
Реклама
Advertisement
Advertisement
Advertisement
Advertisement
Приведенные выше примеры использования слов были взяты из различных источников, чтобы отразить текущее и историческое употребление. Они не отражают мнения YourDictionary.com.
Они не отражают мнения YourDictionary.com.
Связанные статьи
Примеры ионных кристаллов
Ионные кристаллы представляют собой уникальную структуру, созданную, когда два иона электрически притягиваются друг к другу. Эту уникальную связь можно найти в том, что всем нам нравится: в поваренной соли. Погрузитесь в другие примеры ионных кристаллов, найденных по всему миру.
Макс Борн
Макс Борн (1882-1970) немецкий физик. На протяжении своей карьеры он внес жизненно важный вклад в современную теоретическую физику. Его наиболее заметным достижением была демонстрация вероятностной природы основных законов квантовой механики. Он написал несколько классических книг по физике, в том числе The Atomic Theory и The Restless Universe, , а также внес значительный вклад в оптику.
Also Mentioned In
- solid solution
- crys·tal
- annealing
- lattice-work
- orthocomplementation
- meet1
- twin-crystal
- Bragg’s law
- адамантан
- клатрат
- мотив
- период решетки
Words near lattice in the Dictionary
- latter-day
- latter-day-saint
- latter-end
- latterly
- lattermath
- latterness
- lattice
- lattice Boltzmann method
- lattice bridge
- решетчатая корка
- решетчатая константа
- решетчатая энергия
Как добавить оконные решетки, оконные решетки, решетки для французских дверей, решетки для дверей патио в вашем доме.

Набор оконных решеток, решеток, обрешетки и импоста своими руками
Это так же просто, как 1-2-3!
1. Нарежьте полоски ножницами.
2. Наденьте полоски на разъемы
и прикрепите липучку Velcro®, липкую ленту Super Double Stick Tape или клипсы Knife Blade Clips®
3. Прижмите к окну. Мгновенно снимается для очистки.
Insta-Penes Подходит для всех размеров
Подходит для любого стиля окон или дверей, независимо от того, являются ли они раздвижными, поворотными, фиксированными, гаражными воротами или имеют металлические, виниловые или деревянные рамы благодаря сетке крепится прямо к стеклу. Не нужно беспокоиться о сетке специального заказа, которая не подходит – вы обрезаете полоски сетки ножницами, чтобы они подошли к вашему окну. Изделие подойдет к любому окну или двери! Сетка достаточно тонкая, 3/16″ / 0,1875″, чтобы работать со всеми раздвижными окнами или дверями; так что все будет работать так же, как это было. Невозможно сделать это с деревом и т. д.! Нет предела тому, что можно украсить.
Не нужно беспокоиться о сетке специального заказа, которая не подходит – вы обрезаете полоски сетки ножницами, чтобы они подошли к вашему окну. Изделие подойдет к любому окну или двери! Сетка достаточно тонкая, 3/16″ / 0,1875″, чтобы работать со всеми раздвижными окнами или дверями; так что все будет работать так же, как это было. Невозможно сделать это с деревом и т. д.! Нет предела тому, что можно украсить.
Съемные панели Insta
Решетки крепятся непосредственно к стеклу (в основном с внутренней стороны) с помощью самоклеящейся ленты Velcro® с застежкой-липучкой. Нужно всего несколько очень маленьких кусочков 1/4″ вдоль края сетки/стекла. Белые застежки Velcro® скрыты за белой сеткой и едва заметны с противоположной стороны окна.
Также доступны нейлоновые зажимы для лезвий ножей, которые вставляются в конец планки (показана ниже) и под резиновым уплотнителем многих типов окон для неокружающей установки. В каждый комплект входит двадцать зажимов, которые также можно заказать отдельно. Или вы можете прикрепить сетку с помощью суперклейкой двухсторонней ленты. Твой выбор!
Или вы можете прикрепить сетку с помощью суперклейкой двухсторонней ленты. Твой выбор!
ИСПОЛЬЗОВАНИЕ ЗАЖИМА ДЛЯ ЛЕЗВИЯ
Зажим для лезвия (без сиденья)
Зажим для лезвия (для сиденья)
С окантовкой или без нее – на ваш выбор!
Около 1980 г.
Без объемного звука
Полный объемный звук
Каждый тип сетки (показанной выше) имеет свои преимущества. Окантовка (внешняя рама) добавляет жесткости крупным решеткам и позволяет прикреплять застежки-липучки по углам. Некоторые считают, что он также имеет более законченный вид.
Возможно, вы обнаружите, что версия без окантовки лучше подходит для небольших окон и более экономична, поскольку требуется меньше разъемов и планок. NPC, однако, рекомендует полный объемный звук для больших решеток, таких как двери патио или панорамные окна.
Инста-панели долговечны
В отличие от пластиковых мусорных баков, эти решетки не выцветают и не трескаются в течение многих лет, потому что они изготовлены из GEON® — ПВХ-материала, используемого для обшивки домов и виниловых окон. Они никогда не нуждаются в покраске, хотя их можно красить, с использованием только акриловой или латексной краски . ДЕЛАТЬ НЕ ИСПОЛЬЗОВАТЬ КРАСКУ НА ОСНОВЕ РАСТВОРИТЕЛЯ! Большинство аэрозольных красок основаны на растворителе (будьте осторожны). Однако мы рекомендуем избегать темных цветов, если сетки будут находиться под прямыми солнечными лучами в течение многих часов. Более темные цвета поглощают больше солнечного света (эффект альбедо), и это может привести к деформации сетки. Вы можете покрасить только одну сторону, если хотите; внутри перед домом для опрятного вида, многие люди делают. Посетите нашу страницу Галерея для окрашенных заказчиком сеток.
Они никогда не нуждаются в покраске, хотя их можно красить, с использованием только акриловой или латексной краски . ДЕЛАТЬ НЕ ИСПОЛЬЗОВАТЬ КРАСКУ НА ОСНОВЕ РАСТВОРИТЕЛЯ! Большинство аэрозольных красок основаны на растворителе (будьте осторожны). Однако мы рекомендуем избегать темных цветов, если сетки будут находиться под прямыми солнечными лучами в течение многих часов. Более темные цвета поглощают больше солнечного света (эффект альбедо), и это может привести к деформации сетки. Вы можете покрасить только одну сторону, если хотите; внутри перед домом для опрятного вида, многие люди делают. Посетите нашу страницу Галерея для окрашенных заказчиком сеток.
Что мне нужно – как мне начать?
Посмотрите, сколько листов бумаги размером 8 1/2 x 11 дюймов помещается на вашем окне. Большинство панелей (разделенных листов) имеют размер этого листа бумаги или больше. Это вопрос личного вкуса. Нетрудно прикинуть, сколько полосок и соединителей вам понадобится. Наборы имеют различный ассортимент деталей, а в комплекте DLX достаточно деталей, чтобы сделать стандартную 6-футовую дверь патио (по 2 15-литровых решетки в каждой — 3 стекла по ширине и 5 стекол вниз) или несколько окон. В любом случае, не волнуйтесь, вы всегда можете заказать дополнительные детали для отделки всего дома — большинство так и делают! Это весело и легко сделать! А какая разница в ваших окнах!
Наборы имеют различный ассортимент деталей, а в комплекте DLX достаточно деталей, чтобы сделать стандартную 6-футовую дверь патио (по 2 15-литровых решетки в каждой — 3 стекла по ширине и 5 стекол вниз) или несколько окон. В любом случае, не волнуйтесь, вы всегда можете заказать дополнительные детали для отделки всего дома — большинство так и делают! Это весело и легко сделать! А какая разница в ваших окнах!
Основной принцип
Вам нужно будет отрезать две полоски разной длины для каждого окна. Поскольку каждый разъем занимает 1 дюйм (или 25 мм) пространства в каждом направлении, длина полоски зависит от размера вашего окна и количества разъемов, которые вы будете использовать.
ОБЪЕМНОЕ
НЕ ОБЪЕМНОЕ
Изготовление двери патио
Чертежи, которые вам могут понадобиться Помните, что для большинства дверей патио требуется две таких решетки. Ваш фактический размер панели будет отличаться от показанного.
ATRIUM
- Решетка 15 lite с полной окантовкой
- 4 угловых соединителя
- 8 перемычек
- 12 тройников
- 9 полосок по 48″
- 6-дюймовая липучка или 6-дюймовая лента
- Размер панели: 8″ x 12″
СТАНДАРТНАЯ ДВЕРЬ НА ПАТИО
- Решетка 15 lite со сплошным обрамлением
- 4 угловых соединителя
- 8 перемычек
- 12 тройников
- 12 шт. лент шириной 48″
- 6-дюймовая липучка или 6-дюймовая лента
- Размер панели: 10″ x 14″
ДВЕРЬ ДЛЯ БОЛЬШОЙ ПАЦИО
- Решетка 20 lite с полной окантовкой
- 4 угловых соединителя
- 12 поперечных соединителей
- 14 тройников
- 15 шт. лент шириной 48″
- 6-дюймовая липучка или 6-дюймовая лента
- Размер панели: 10″ x 14″
Вы также можете создавать «Стили прерий» или современные разделенные панели с Insta-Pane, как показано выше. Этот стиль популяризировал архитектор Фрэнк Ллойд Райт. Он также используется сегодня некоторыми производителями новых окон.
Этот стиль популяризировал архитектор Фрэнк Ллойд Райт. Он также используется сегодня некоторыми производителями новых окон.
Только Insta-Panes позволяет разделить обычные окна на любые прямоугольные формы и размеры по вашему выбору! Для этого стиля нет компьютерной помощи или подробных инструкций.
Вы даже можете сделать полукруглое окно, используя только полоски и липучки. Просто отрежьте углы для основания и прикрепите липучки Velcro® к обоим концам полос — прикрепите к стеклу!
Примечание
Алмазные сетки нельзя изготавливать с этим изделием.
P.S. Нужна дополнительная помощь?
Использовать калькулятор Купить
Что можно делать с набором для пробоотборника?
Ниже приведены несколько примеров того, что можно украсить с помощью комплекта для пробоотборника. Все сделано в режиме Non-Surround. КУПИТЬ СЕЙЧАС.
Все еще сомневаетесь?… Попробуйте пробоотборник!
Попробуйте набор для проб всего за 59,95 долларов США + бесплатная доставка. Он украсит около 12 квадратных футов стекла, как показано выше! И если вы не удовлетворены, верните все разъемы и неразрезанные детали для возврата денег.
Он украсит около 12 квадратных футов стекла, как показано выше! И если вы не удовлетворены, верните все разъемы и неразрезанные детали для возврата денег.
Или дверь патио. Заказывайте комплекты или только те детали, которые вам нужны. Будь то окна или двери, вы в конечном итоге закажете больше для всего дома — так делает большинство людей.
Мы отправляем заказы через ПРИОРИТЕТНУЮ ПОЧТУ USPS.
[email protected] или вы можете заказать на нашей странице цен/заказа.
Velcro® — зарегистрированная торговая марка VELCRO Industries B.V.
Geon® — зарегистрированная торговая марка The Geon Company
Виниловые окна Endure™ | Лучшие виниловые окна ProVia
Потрясающая энергоэффективность
Вам нечасто приходится покупать окна для своего дома, но когда вы это делаете, вам нужны варианты, которые сделают ваш дом выделяющимся. Домовладельцы ищут окна, которые улучшают внешний вид, обеспечивая при этом максимальную энергоэффективность и комфорт.
Виниловые окна Endure компании ProVia отвечают всем этим требованиям, обеспечивая беспрецедентную индивидуализацию в сочетании с выдающимся качеством и энергоэффективностью.
Для виниловых окон Endure компания ProVia выбрала оптимальные технологические уровни, чтобы создать окно, которое будет постоянно работать с максимальной производительностью. Окна Endure обеспечивают все, что вы ожидаете от высокоэффективных виниловых окон, сертифицированных ENERGY STAR®, потребляя гораздо меньше энергии, чтобы сохранять тепло зимой, прохладу летом и обеспечивать больший комфорт круглый год.
Окна Endure обеспечивают максимальную энергоэффективность, демонстрируя потрясающую красоту и оправдывая ожидания лучших виниловых окон.
Глубина рамы 3¼ дюйма
Винил SunShield®
1-дюймовый стеклопакет ComforTech™ DLA-UV с изоляцией
ФайнЛайн™
Окна Endure отличаются новой инновационной сваркой. процесс под названием FineLine Technology. Сварка FineLine
угол эстетически более привлекателен, чем традиционный
сварной уголок.
процесс под названием FineLine Technology. Сварка FineLine
угол эстетически более привлекателен, чем традиционный
сварной уголок.
Утеплитель Неопор®
Neopor — это жесткая пенопластовая изоляция из графитового полистирола, обеспечивающая максимальную эффективность и устойчивость строительных материалов.
Полноэкранный экструдированный алюминий с BetterVue® Сетка из стекловолокна
INERGY® Термическое усиление
Innergy — это инновационная энергоэффективная альтернатива алюминий с дополнительными изоляционными свойствами, делающими его 700 раз лучше.
Уплотнение барьерного ребра и колбы уплотнения
Утепление – очень важная часть предотвращения проникновения воздуха в ваш дом. Окна ProVia имеют уплотнитель на раме и створке, что обеспечивает хорошее уплотнение в важных местах, через которые может проходить воздух.
Окна ProVia имеют уплотнитель на раме и створке, что обеспечивает хорошее уплотнение в важных местах, через которые может проходить воздух.
Скрыть/показать аннотации Функциональность анимации Сбросить модель
Прокрутите, чтобы увеличить Щелкните левой кнопкой мыши, чтобы повернуть Щелкните правой кнопкой мыши, чтобы панорамировать
Key
FeaturesUncompromised durability and performance
- Low maintenance
- Superior weatherability
- Outstanding color retention
- More durable than competitive products
- Exceeds standards for strength and color
- Maximum number of options для стиля окна, цвета, стекла и т.
 д.
д.
Endure
стилей оконВарианты дизайна для всего дома
ДВУХПОДВЕСНОЙ
Слайдер
Створка и тент
Хоппер
Картина
Сад
Бэй и Лук
Формы
Окно
ЦВЕТАИндивидуальная настройка каждой комнаты
Домовладельцы считают виниловые окна Endure одними из лучших доступных виниловых окон, отчасти потому, что их можно настроить так, чтобы они сочетались с цветами интерьера каждой комнаты в вашем доме. . Выберите один из популярных цветов под дерево для внутренней отделки и несколько вариантов окраски кузова.
Цвет интерьера
Classic Oakdark Oaktraditional Cherrywhitebeigesandstonewhite WoodgrainПредыдущий
Следующая
.

Обновление до окрашенного кузова
ФурнитураProVia предлагает варианты фурнитуры, которые позволяют сделать ваши виниловые окна такими уникальными, как вам нравится.
Двойной подвес и слайдер
Белая оконная фурнитура Endure™ для двустворчатых окон и раздвижных окон Оконная фурнитура Endure™ Beige для двустворчатых окон и раздвижных окон Оконная фурнитура из песчаника Endure™ для двустворчатых окон и раздвижных окон Оконная фурнитура Endure™ Coppertone для двустворчатых окон и раздвижных окон Оконная фурнитура Endure™ Flat Bronze для двустворчатых окон и раздвижных окон со встроенными наклонными защелками DualTech™ Оконная фурнитура Endure™ Satin Nickel для двустворчатых окон и раздвижных окон со встроенными наклонными защелками DualTech™ Античная латунь — опционально, со встроенными защелками DualTech™.Створка и навес
Белая оконная фурнитура Endure™ для оконных створок и навесов Оконная фурнитура Endure™ Beige для оконных створок и навесов Оконная фурнитура из песчаника Endure™ для створчатых окон и навесов Оконная фурнитура Endure™ Coppertone для оконных створок и навесов Оконная фурнитура Endure™ Flat Bronze для оконных створок и навесов Оконная фурнитура Endure™ Satin Nickel для створчатых окон и навесов Оконная фурнитура Endure™ Antique Brass для створчатых окон и навесов Стекло ОпцииШаг за пределы прозрачного стекла
Деревянные внутренние окна ProVia Aeris не будут полными без индивидуализированных стекол, которые еще больше повысят привлекательность бордюра.
прозрачное стекло
Витражи
декоративное стекло
Тонированные стекла
Оконные сетки
Внутренние жалюзи
Максимизируйте комфорт вашего домаУзнайте об оконной технологии, обеспечивающей энергоэффективность наших окон
кликните сюда
Окно
Варианты экранаУлучшенная четкость и обслуживание
На изображениях ниже показаны крупным планом различные типы сетки экрана. Если смотреть издалека, сетка не так заметна
BetterVue®
Стекловолоконная сетка
Стандартно для всех окон Aeris
- Рама из экструдированного алюминия со стекловолоконной сеткой BetterVue
- Прочный и огнестойкий
- Улучшенная оптическая прозрачность; защищает от воды и защищает от грязи и копоти
- Гидрофобное покрытие улучшает оптическую прозрачность, отталкивает воду и защищает от грязи и грязи
- Легко снимается для очистки и обслуживания
SeeVue®
Сетка из нержавеющей стали
Вариант с усиленной сеткой
- Подходит для домашних животных
- Рама из экструдированного алюминия с сеткой из нержавеющей стали
- С черным покрытием для улучшения видимости и вентиляции
- Прочнее стандартной сетки от насекомых
FlexScreen®
Едва заметный и почти неразрушимый
- Рама из пружинной стали с покрытием из ПВХ, не требующая крепежных деталей
- Простая установка
- Прочная рама, которая не скручивается и не ломается, как традиционные оконные сетки
- Устойчива к вмятинам и царапинам
- 8 Позволяет проникать большему количеству дневного света, значительно улучшая обзор через стекло
- Доступен с сеткой BetterVue® или прочной стекловолоконной сеткой
Прочная сетка из стекловолокна
Алюминиевая сетка
Профессиональная
Оконные накладкиИдеальный последний штрих
Оконные наличники не должны быть второстепенными, это деталь, которую установщик должен вырезать, покрасить или окрасить, а затем установить. С системой отделки ProVia MasterFit™ тяжелая работа выполняется на нашем заводе, где мы можем гарантировать точное, индивидуальное и долговечное заводское покрытие.
С системой отделки ProVia MasterFit™ тяжелая работа выполняется на нашем заводе, где мы можем гарантировать точное, индивидуальное и долговечное заводское покрытие.
Endure WINDOW
ГАЛЕРЕЯОкна ProVia на дисплее
Get
InspiredПосетите нашу галерею окон, чтобы увидеть другие оконные изделия ProVia
Исследовать
Посмотреть сравнение брендов окон
Взгляните поближе
Откройте нашу брошюру
Endure для всех опцийОграниченная пожизненная
ГарантияАбсолютное спокойствие
ProVia поддерживает качество своей продукции, предоставляя передаваемую пожизненную ограниченную гарантию, которая переходит к одному последующему владельцу дома.
Учить больше
вдохновил начать свой проект ?Посетите Центр проектирования
, чтобы настроить свой продукт или связаться с дилером.
 Благодаря размеру полотна можно создать эксклюзивный и привлекательный рисунок.
Благодаря размеру полотна можно создать эксклюзивный и привлекательный рисунок. И он будет совершенно прав. При непредвиденных обстоятельствах с такой решеткой не получится воспользоваться окном, как запасным выходом.
И он будет совершенно прав. При непредвиденных обстоятельствах с такой решеткой не получится воспользоваться окном, как запасным выходом. Чтобы вы получили его без задержек, в штате работают более 50 человек, каждый из которых профи. Доставляем по Москве и Московской области.
Чтобы вы получили его без задержек, в штате работают более 50 человек, каждый из которых профи. Доставляем по Москве и Московской области. Гарантия распространяется на все виды решеток и на установку.
Гарантия распространяется на все виды решеток и на установку.