Рисунок многоугольника: Рисунок из многоугольников — 64 фото
Как выглядит многоугольник. Многоугольники и их свойства. Многоугольником называется простая замкнутая
Словари. Энциклопедии. История. Литература. Русский язык » Словарь » Как выглядит многоугольник. Многоугольники и их свойства. Многоугольником называется простая замкнутая
Многоугольник — это геометрическая фигура, ограниченная замкнутой ломаной линией , не имеющей самопересечений.
Звенья ломаной называются сторонами многоугольника , а её вершины — вершинами многоугольника .
Углами многоугольника называются внутренние углы, образованные соседними сторонами. Число углов многоугольника равно числу его вершин и сторон.
Многоугольникам даются названия по количеству сторон. Многоугольник с наименьшим количеством сторон называется треугольником, он имеет всего три стороны. Многоугольник с четырьмя сторонами называется четырёхугольником, с пятью — пятиугольником и т. д.
Обозначение многоугольника составляют из букв, стоящих при его вершинах, называя их по порядку (по часовой или против часовой стрелки).
В пятиугольнике ABCDE точки A , B , C , D и E — это вершины пятиугольника, а отрезки AB , BC , CD , DE и EA — стороны пятиугольника.
Выпуклые и вогнутые
Многоугольник называется выпуклым , если ни одна из его сторон, продолженная до прямой линии, его не пересекает. В обратном случае многоугольник называется вогнутым :
Периметр
Сумма длин всех сторон многоугольника называется его периметром .
Периметр многоугольника ABCDE равен:
AB + BC + CD + DE + EA
Если у многоугольника равны все стороны и все углы, то его называют правильным . Правильными многоугольниками могут быть только выпуклые многоугольники.
Диагональ
Диагональ многоугольника — это отрезок , соединяющий вершины двух углов, не имеющих общей стороны.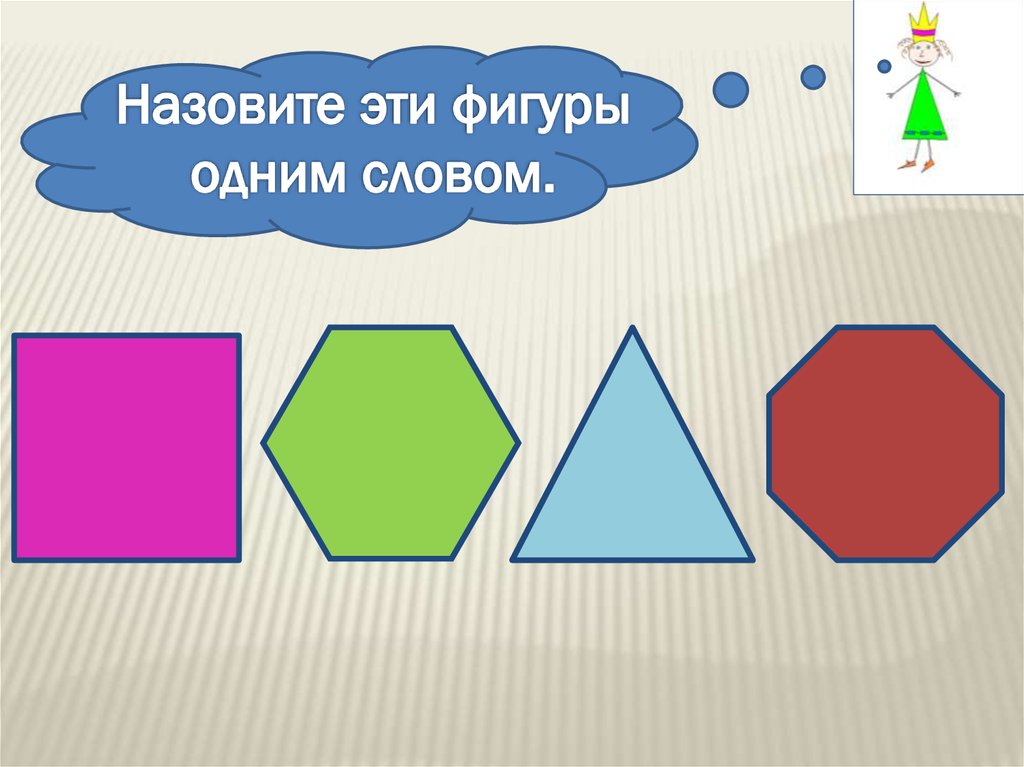
Единственным многоугольником, который не имеет ни одной диагонали, является треугольник, так как в нём нет углов, не имеющих общих сторон.
Если из какой-нибудь вершины многоугольника провести все возможные диагонали, то они разделят многоугольник на треугольники:
Треугольников будет ровно на два меньше, чем сторон:
t = n — 2
где t — это количество треугольников, а n — количество сторон.
Разделение многоугольника на треугольники с помощью диагоналей используется для нахождения площади многоугольника, так как чтобы найти площадь какого-нибудь многоугольника, нужно разбить его на треугольники, найти площадь этих треугольников и полученные результаты сложить .
Виды многоугольников:
Четырехугольники
Четырехугольники , соответственно, состоят из 4-х сторон и углов.
Стороны и углы, расположенные напротив друг друга, называются противоположными .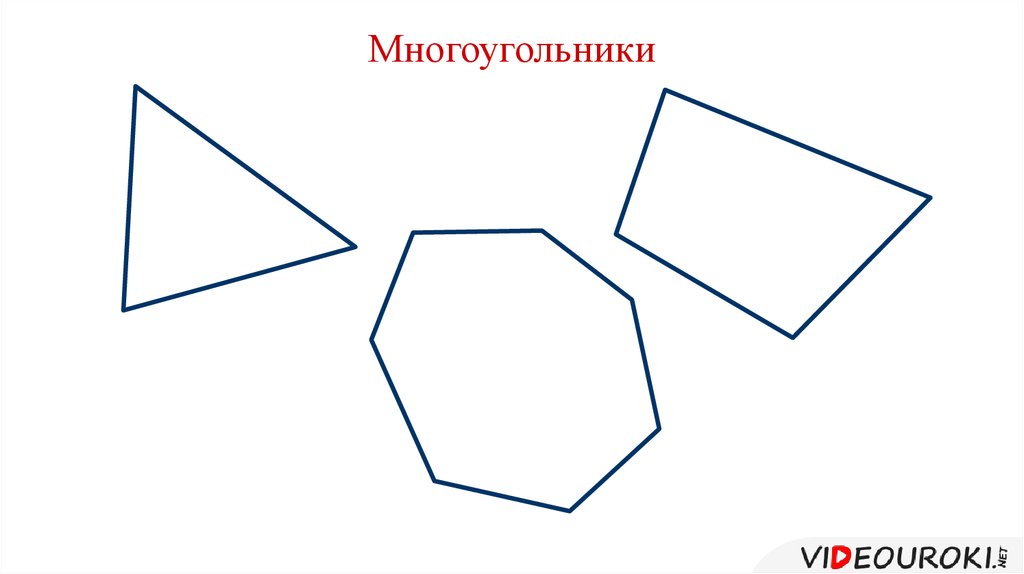
Диагонали делят выпуклые четырехугольники на треугольники (см. на рисунке).
Сумма углов выпуклого четырехугольника равна 360° (по формуле: (4-2)*180°).
Параллелограммы
Параллелограмм — это выпуклый четырехугольник с противоположными параллельными сторонами (на рис. под номером 1).
Противоположные стороны и углы в параллелограмме всегда равны.
А диагонали в точке пересечения делятся пополам.
Трапеции
Трапеция — это тоже четырехугольник, и в трапеции параллельны только две стороны, которые называются основаниями . Другие стороны — это боковые стороны .
Трапеция на рисунке под номером 2 и 7.
Как и в треугольнике:
Если боковые стороны равны, то трапеция — равнобедренная ;
Если один из углов прямой, то трапеция — прямоугольная.
Средняя линия трапеции равна полусумме оснований и параллельна им.
Ромб
Ромб — это параллелограмм, у которого все стороны равны.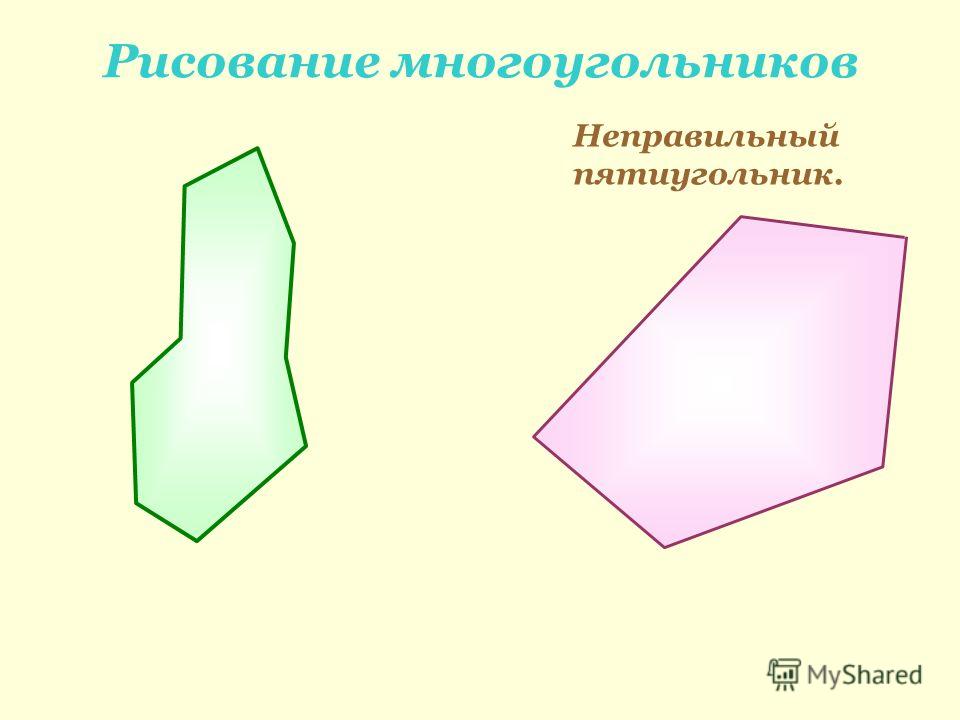
Помимо свойств параллелограмма, ромбы имеют своё особое свойство — диагонали ромба перпендикулярны друг другу и делят углы ромба пополам .
На рисунке ромб под номером 5.
Прямоугольники
Прямоугольник — это параллелограмм, у которого каждый угол прямой (см. на рис. под номером 8).
Помимо свойств параллелограмма, прямоугольники имеют своё особое свойство — диагонали прямоугольника равны .
Квадраты
Квадрат — это прямоугольник, у которого все стороны равны (№4).
Обладает свойствами прямоугольника и ромба (так как все стороны равны).
§ 1 Понятие треугольника
В этом уроке Вы познакомитесь с такими фигурами как треугольник и многоугольник.
Если три точки, не лежащие на одной прямой, соединить отрезками, то получится треугольник. Треугольник имеет три вершины и три стороны.
Перед вами треугольник АВС, он имеет три вершины (точку А, точку В и точку С) и три стороны (АВ, АС и СВ).
Кстати, эти же стороны можно называть и по-другому:
АВ=ВА, АС=СА, СВ=ВС.
Стороны треугольника образуют в вершинах треугольника три угла. На рисунке вы видите угол А, угол В, угол С.
Таким образом, треугольник — это геометрическая фигура, образованнаятремя отрезками, которые соединяют три, не лежащие на одной прямой, точки.
§ 2 Понятие многоугольника и его виды
Кроме треугольников, существуют четырехугольники, пятиугольники, шестиугольники и так далее. Одним словом их можно назвать многоугольники.
На рисунке Вы видите четырехугольник DMKE.
Точки D, M, K и E являются вершинами четырехугольника.
Отрезки DM, MK, KE, ED являются сторонами данного четырехугольника. Так же, как и в случае с треугольником, стороны четырехугольника образуют в вершинах четыре угла, как Вы догадались, отсюда и название — четырехугольник. У данного четырехугольника вы видите на рисунке угол D, угол M, угол K и угол E.
А какие четырехугольники Вам уже известны?
Квадрат и прямоугольник! Каждый из них имеет по четыре угла и четыре стороны.
Еще один вид многоугольников — пятиугольник.
Точки O, P, X, Y, Т являются вершинами пятиугольника, а отрезки TO, OP, PX, XY, YT являются сторонами данного пятиугольника. У пятиугольника соответственно пять углов и пять сторон.
Как Вы считаете, сколько углов и сколько сторон у шестиугольника? Правильно, шесть! Рассуждая аналогичным образом, можно сказать, сколько сторон, вершин или углов имеет тот или иной многоугольник. И можно сделать вывод, что треугольник — это тоже многоугольник, у которого имеется ровно три угла, три стороны и три вершины.
Таким образом, на этом уроке Вы познакомились с такими понятиями как треугольник и многоугольник. Узнали, что треугольник имеет 3 вершины, 3 стороны и 3 угла, четырехугольник — 4 вершины, 4 стороны и 4 угла, пятиугольник — соответственно 5 сторон, 5 вершин,5 углов и так далее.
Список использованной литературы:
- Математика 5 класс. Виленкин Н.Я., Жохов В.И. и др. 31-е изд., стер. — М: 2013.
- Дидактические материалы по математике 5 класс.
 Автор — Попов М.А. — 2013 год
Автор — Попов М.А. — 2013 год - Вычисляем без ошибок. Работы с самопроверкой по математике 5-6 классы. Автор — Минаева С.С. — 2014 год
- Дидактические материалы по математике 5 класс. Авторы: Дорофеев Г.В., Кузнецова Л.В. — 2010 год
- Контрольные и самостоятельные работы по математике 5 класс. Авторы — Попов М.А. — 2012 год
- Математика. 5 класс: учеб. для учащихся общеобразоват. учреждений / И. И. Зубарева, А. Г. Мордкович. — 9-е изд., стер. — М.: Мнемозина, 2009
Владение терминологией, а также знание свойств различных геометрических фигур помогут в решении многих задач по геометрии. Изучая такой раздел как планиметрия, учащийся не редко встречает термин “многоугольник”. Какую фигуру характеризует данное понятие?
Многоугольник – определение геометрической фигуры
Замкнутая ломаная линия, все участки которой лежат в одной плоскости и не имеют участков самопересечения, образует геометрическую фигуру под названием многоугольник. Число звеньев ломаной должно быть не менее 3-х.
В ходе решения задач с участием многоугольника, нередко фигурируют такие понятия как:
- Сторона многоугольника. Данный термин характеризует отрезок (звено) ломаной цепи искомой фигуры.
- Угол многоугольника (внутренний) – угол, который формируют 2 смежных звена ломаной.
- Вершина многоугольника определяется как вершина ломаной.
- Диагональ многоугольника – отрезок, соединяющие любые 2 вершины (кроме соседних) многоугольной фигуры.
При этом число звеньев и число вершин ломаной в пределах одного многоугольника совпадают. В зависимости от количества углов (или отрезков ломаной соответственно) определяется и вид многоугольника:
- 3 угла – треугольник.
- 4 угла – четырехугольник.
- 5 углов – пятиугольник и т.д.
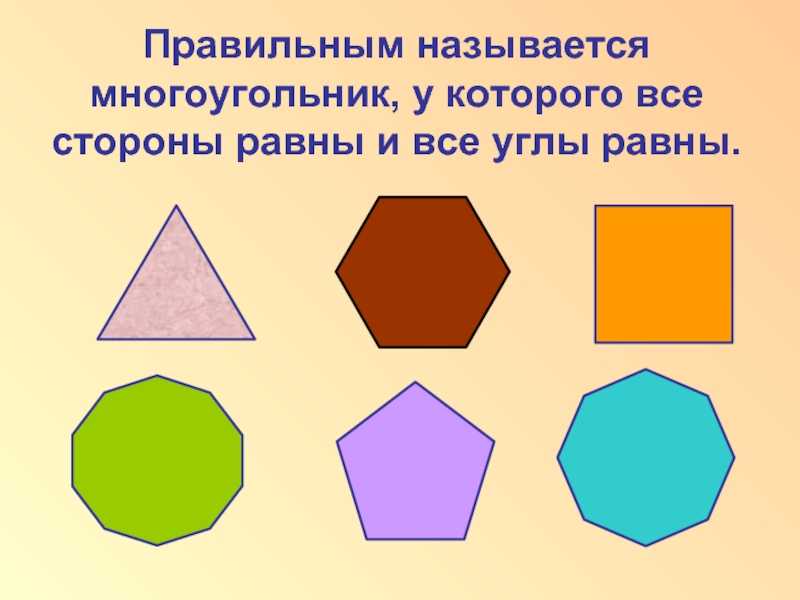
Если многоугольная фигура имеет равные углы и соответственно стороны, то говорят, что данный многоугольник правильный.
Типы многоугольников
Все многоугольные геометрические фигуры разделяются на 2 типа – выпуклые и вогнутые.
- Если любая из сторон многоугольника после продолжения до прямой не образует с собственно фигурой точек пересечения, перед вами выпуклая многоугольная фигура.
- Если после продолжения стороны (любой) полученная прямая пересекает многоугольник, речь идет о вогнутом многоугольнике.
Свойства многоугольника
Вне зависимости от того, является изучаемая многоугольная фигура правильной или нет, она обладает приведенными ниже свойствами. Так:
- Ее внутренние углы суммарно образуют (p – 2)*π, где
π – радианная мера развернутого угла, соответствует 180°,
p – число углов (вершин) многоугольной фигуры (p-угольника).
- Количество диагоналей всякой многоугольной фигуры определяется из соотношения p*(p – 3) / 2, где
p – число сторон p-угольника.
На этом уроке мы приступим уже к новой теме и введем новое для нас понятие «многоугольник». Мы рассмотрим основные понятия, связанные с многоугольниками: стороны, вершины углы, выпуклость и невыпуклость. Затем докажем важнейшие факты, такие как теорема о сумме внутренних углов многоугольника, теорема о сумме внешних углов многоугольника. В итоге, мы вплотную подойдем к изучению частных случаев многоугольников, которые будут рассматриваться на дальнейших уроках.
Мы рассмотрим основные понятия, связанные с многоугольниками: стороны, вершины углы, выпуклость и невыпуклость. Затем докажем важнейшие факты, такие как теорема о сумме внутренних углов многоугольника, теорема о сумме внешних углов многоугольника. В итоге, мы вплотную подойдем к изучению частных случаев многоугольников, которые будут рассматриваться на дальнейших уроках.
Тема: Четырехугольники
Урок: Многоугольники
В курсе геометрии мы изучаем свойства геометрических фигур и уже рассмотрели простейшие из них: треугольники и окружности. При этом мы обсуждали и конкретные частные случаи этих фигур, такие как прямоугольные, равнобедренные и правильные треугольники. Теперь пришло время поговорить о более общих и сложных фигурах — многоугольниках .
С частным случаем многоугольников мы уже знакомы — это треугольник (см. Рис. 1).
Рис. 1. Треугольник
В самом названии уже подчеркивается, что это фигура, у которой три угла. Следовательно, в многоугольнике их может быть много, т. е. больше, чем три. Например, изобразим пятиугольник (см. Рис. 2), т.е. фигуру с пятью углами.
е. больше, чем три. Например, изобразим пятиугольник (см. Рис. 2), т.е. фигуру с пятью углами.
Рис. 2. Пятиугольник. Выпуклый многоугольник
Определение. Многоугольник — фигура, состоящая из нескольких точек (больше двух) и соответствующего количества отрезков, которые их последовательно соединяют. Эти точки называются вершинами многоугольника, а отрезки — сторонами . При этом никакие две смежные стороны не лежат на одной прямой и никакие две несмежные стороны не пересекаются.
Определение. Правильный многоугольник — это выпуклый многоугольник, у которого все стороны и углы равны.
Любой многоугольник разделяет плоскость на две области: внутреннюю и внешнюю. Внутреннюю область также относят к многоугольнику .
Иными словами, например, когда говорят о пятиугольнике , имеют в виду и всю его внутреннюю область, и границу. А ко внутренней области относятся и все точки, которые лежат внутри многоугольника, т. е. точка тоже относится к пятиугольнику (см. Рис. 2).
е. точка тоже относится к пятиугольнику (см. Рис. 2).
Многоугольники еще иногда называют n-угольниками, чтобы подчеркнуть, что рассматривается общий случай наличия какого-то неизвестного количества углов (n штук).
Определение. Периметр многоугольника — сумма длин сторон многоугольника.
Теперь надо познакомиться с видами многоугольников. Они делятся на выпуклые и невыпуклые . Например, многоугольник, изображенный на Рис. 2, является выпуклым, а на Рис. 3 невыпуклым.
Рис. 3. Невыпуклый многоугольник
Определение 1. Многоугольник называется выпуклым , если при проведении прямой через любую из его сторон весь многоугольник лежит только по одну сторону от этой прямой. Невыпуклыми являются все остальные многоугольники .
Легко представить, что при продлении любой стороны пятиугольника на Рис. 2 он весь окажется по одну сторону от этой прямой, т.е. он выпуклый. А вот при проведении прямой через в четырехугольнике на Рис. 3 мы уже видим, что она разделяет его на две части, т.е. он невыпуклый.
3 мы уже видим, что она разделяет его на две части, т.е. он невыпуклый.
Но существует и другое определение выпуклости многоугольника.
Определение 2. Многоугольник называется выпуклым , если при выборе любых двух его внутренних точек и при соединении их отрезком все точки отрезка являются также внутренними точками многоугольника.
Демонстрацию использования этого определения можно увидеть на примере построения отрезков на Рис. 2 и 3.
Определение. Диагональю многоугольника называется любой отрезок, соединяющий две не соседние его вершины.
Для описания свойств многоугольников существуют две важнейшие теоремы об их углах: теорема о сумме внутренних углов выпуклого многоугольника и теорема о сумме внешних углов выпуклого многоугольника . Рассмотрим их.
Теорема. О сумме внутренних углов выпуклого многоугольника (n -угольника).
Где — количество его углов (сторон).
Доказательство 1. Изобразим на Рис. 4 выпуклый n-угольник.
4 выпуклый n-угольник.
Рис. 4. Выпуклый n-угольник
Из вершины проведем все возможные диагонали. Они делят n-угольник на треугольника, т.к. каждая из сторон многоугольника образует треугольник, кроме сторон, прилежащих к вершине . Легко видеть по рисунку, что сумма углов всех этих треугольников как раз будет равна сумме внутренних углов n-угольника. Поскольку сумма углов любого треугольника — , то сумма внутренних углов n-угольника:
Что и требовалось доказать.
Доказательство 2. Возможно и другое доказательство этой теоремы. Изобразим аналогичный n-угольник на Рис. 5 и соединим любую его внутреннюю точку со всеми вершинами.
Рис. 5.
Мы получили разбиение n-угольника на n треугольников (сколько сторон, столько и треугольников). Сумма всех их углов равна сумме внутренних углов многоугольника и сумме углов при внутренней точке, а это угол . Имеем:
Что и требовалось доказать.
Доказано.
По доказанной теореме видно, что сумма углов n-угольника зависит от количества его сторон (от n). Например, в треугольнике , а сумма углов . В четырехугольнике , а сумма углов — и т.д.
Например, в треугольнике , а сумма углов . В четырехугольнике , а сумма углов — и т.д.
Теорема. О сумме внешних углов выпуклого многоугольника (n -угольника).
Где — количество его углов (сторон), а , …, — внешние углы.
Доказательство. Изобразим выпуклый n-угольник на Рис. 6 и обозначим его внутренние и внешние углы.
Рис. 6. Выпуклый n-угольник с обозначенными внешними углами
Т.к. внешний угол связан со внутренним как смежные, то и аналогично для остальных внешних углов. Тогда:
В ходе преобразований мы воспользовались уже доказанной теоремой о сумме внутренних углов n-угольника .
Доказано.
Из доказанной теоремы следует интересный факт, что сумма внешних углов выпуклого n-угольника равна от количества его углов (сторон). Кстати, в отличие от суммы внутренних углов.
Список литературы
- Александров А.Д. и др. Геометрия, 8 класс. — М.: Просвещение, 2006.
- Бутузов В.Ф., Кадомцев С.
 Б., Прасолов В.В. Геометрия, 8 класс. — М.: Просвещение, 2011.
Б., Прасолов В.В. Геометрия, 8 класс. — М.: Просвещение, 2011. - Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. — М.: ВЕНТАНА-ГРАФ, 2009.
- Profmeter.com.ua ().
- Narod.ru ().
- Xvatit.com ().
Домашнее задание
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
| Справочник по математике | Геометрия (Планиметрия) | Многоугольники |
| Определение многоугольника |
| Диагонали n – угольника |
| Внешний угол многоугольника |
| Свойства углов треугольника |
| Свойства углов многоугольника |
| Свойства углов правильного n – угольника |
| Доказательства теорем о свойствах углов многоугольника |
Определение многоугольника
Рассмотрим n отрезков
| [A1 A2], [A2 A3], … , [An An +1] | (1) |
причём таких, что два любых отрезка, имеющих общий конец, не лежат на одной прямой (рис. 1).
1).
Рис. 1
Определение 1. Ломаной линией с n звеньями называют фигуру L, составленную из отрезков (1), то есть фигуру, заданную равенством
L = [A1 A2] U [A2 A3] U …
… U [An An +1]
В случае, когда точки A1 и An +1 совпадают, ломаную линию называют замкнутой ломаной линией (рис. 2), в противном случае её называют незамкнутой (рис.1).
Рис. 2
Определение 2. Многоугольником называют часть плоскости, ограниченную замкнутой ломаной линией без самопересечений (рис. 3). Отрезки, составляющие ломаную линию (звенья), называют сторонами многоугольника. Концы отрезков называют вершинами многоугольника.
Рис. 3
Определение 3. Многоугольник называют n – угольником, если он имеет n сторон.
Таким образом, многоугольник, имеющий 3 стороны, называют треугольником, многоугольник, имеющий 4 стороны, называют четырёхугольником и т.д.
Определение 4 . Периметром многоугольника называют сумму длин всех сторон многоугольника.
Величину, равную половине периметра, называют полупериметром.
Диагонали n — угольника
| Фигура | Рисунок | Описание |
| Диагональ многоугольника | Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника | |
| Диагонали n – угольника, выходящие из одной вершины | Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника | |
| Все диагонали n – угольника | Число диагоналей n – угольника равно |
| Диагональ многоугольника |
Диагональю многоугольника называют отрезок, соединяющий две несоседние вершины многоугольника |
| Диагонали n – угольника, выходящие из одной вершины |
Диагонали, выходящие из одной вершины n – угольника, делят n – угольник на n – 2 треугольника |
| Все диагонали n – угольника |
Число диагоналей n – угольника равно |
Внешний угол многоугольника
Определение 5 . Два угла называют смежными, если они имеют общую сторону, и их сумма равна 180° (рис.1).
Два угла называют смежными, если они имеют общую сторону, и их сумма равна 180° (рис.1).
Рис.1
Определение 6 . Внешним углом многоугольника называют угол, смежный с внутренним углом многоугольника (рис.2).
Рис.2
Замечание. Мы рассматриваем только выпуклые многоугольникивыпуклые многоугольники.
Свойства углов треугольника
| Фигура | Рисунок | Формулировка теоремы |
| Углы треугольника | Сумма углов треугольника равна 180° α + β + γ = 180° Посмотреть доказательство | |
| Внешний угол треугольника | Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним δ = α + β Посмотреть доказательство |
| Углы треугольника |
Сумма углов треугольника равна 180° α + β + γ = 180° Посмотреть доказательство |
| Внешний угол треугольника |
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним δ = α + β Посмотреть доказательство |
Свойства углов многоугольника
| Фигура | Рисунок | Формулировка теоремы |
| Углы n – угольника | Сумма углов многоугольника равна Посмотреть доказательство | |
| Внешние углы n – угольника | Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360° Посмотреть доказательство |
| Углы n – угольника |
Сумма углов многоугольника равна Посмотреть доказательство |
| Внешние углы n – угольника |
Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360° Посмотреть доказательство |
Свойства углов правильного n – угольника
| Фигура | Рисунок | Формулировка теоремы |
| Углы правильного n – угольника | Все углы правильного n – угольника равны | |
| Внешние углы правильного n – угольника | Все внешние углы правильного |
| Углы правильного n – угольника |
Все углы правильного n – угольника равны |
| Внешние углы правильного n – угольника |
Все внешние углы правильного |
Доказательства свойств углов многоугольника
Теорема 1. В любом треугольнике сумма углов равна 180°.
В любом треугольнике сумма углов равна 180°.
Доказательство. Проведем, например, через вершину B произвольного треугольника ABC прямую DE, параллельную прямой AC, и рассмотрим полученные углы с вершиной в точке B (рис. 3).
Рис.3
Углы ABD и BAC равны как внутренние накрест лежащие. По той же причине равны углы ACB и CBE. Поскольку углы ABD, ABC и CBE в сумме составляют развёрнутый угол, то и сумма углов треугольника ABC равна 180°. Теорема доказана.
Теорема 2. Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Доказательство. Проведём через вершину C прямую CE, параллельную прямой AB, и продолжим отрезок AC за точку C (рис.4).
Рис.4
Углы ABC и BCE равны как внутренние накрест лежащие. Углы BAC и ECD равны как соответственные равны как соответственные. Поэтому внешний угол BCD равен сумме углов BAC и ABC. Теорема доказана.
Поэтому внешний угол BCD равен сумме углов BAC и ABC. Теорема доказана.
Замечание. Теорема 1 является следствием теоремы 2.
Теорема 3. Сумма углов n – угольника равна
Доказательство. Выберем внутри n – угольника произвольную точку O и соединим её со всеми вершинами n – угольника (рис. 5).
Рис.5
Получим n треугольников:
OA1A2, OA2A3, … OAnA1
Сумма углов всех этих треугольников равна сумме всех внутренних углов n – угольника плюс сумма всех углов с вершиной в точке O. Поэтому сумма всех углов n – угольника равна
что и требовалось доказать.
Теорема 4. Сумма внешних углов n – угольника, взятых по одному у каждой вершины, равна 360°.
Доказательство. Рассмотрим рисунок 6.
Рис.6
В соответствии рисунком 6 справедливы равенства
Теорема доказана.
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Polygon Patterns — Etsy.de
Etsy больше не поддерживает старые версии вашего веб-браузера, чтобы обеспечить безопасность пользовательских данных. Пожалуйста, обновите до последней версии.
Воспользуйтесь всеми преимуществами нашего сайта, включив JavaScript.
Найдите что-нибудь памятное, присоединяйтесь к сообществу, делающему добро.
(
1000+ релевантных результатов,
с рекламой
Продавцы, желающие расширить свой бизнес и привлечь больше заинтересованных покупателей, могут использовать рекламную платформу Etsy для продвижения своих товаров. Вы увидите результаты объявлений, основанные на таких факторах, как релевантность и сумма, которую продавцы платят за клик. Узнать больше.
)
Вы увидите результаты объявлений, основанные на таких факторах, как релевантность и сумма, которую продавцы платят за клик. Узнать больше.
)
Polygon: Оптогенетика с клеточным разрешением и фотостимуляция
Связаться с нами
Polygon
Осветитель DMD Pattern
для целевой фотостимуляции
DMD Pattern Illuminator
для целевой фотостимуляции 90 003
Многоугольник
- Обзор/функции
- Применение
- Модели
- Ресурсы
- Свяжитесь с нами
Обзор/Функции
600+ лабораторий по всему миру, более 100 публикаций с использованием Polygon
Лидирующий на рынке осветитель Polygon DMD компании Mightex обеспечивает точное пространственно-временное управление светом с субклеточным разрешением, что делает его идеальным инструментом освещения для исследований в области наук о жизни.
Оптогенетика с клеточным разрешением и фотостимуляция
Одновременное многозональное освещение
Субклеточное разрешение
Совместимость с любым микроскопом
Полигон Брошюра и технические характеристики
Современная технология освещения
В Polygon используется технология цифрового зеркального устройства (DMD) для одновременного освещения нескольких областей. DMD состоит из сотен тысяч микрозеркал, которые можно включать по отдельности, чтобы отражать свет на образец. Таким образом, вы можете управлять каждым зеркалом, чтобы управлять областью (областями) освещения и создавать любое количество узоров разного размера. Осветитель полигона Polygon DMD можно установить на бесконечном пути любого микроскопа.
Основные характеристики многоугольника
Выберите освещение отдельных клеток, экспрессирующих ChR2, в срезе с помощью многоугольника (любезно предоставлено Мэтью Траном и доктором Блейком Ричардсом, Университет Макгилла).
Одновременная оптогенетическая стимуляция отдельных клеток или субклеточных компонентов
Полигон позволяет ученым точно контролировать, где свет будет падать на их образец. С субклеточным разрешением Polygon может одновременно освещать любые клеточные элементы любой формы и размера на своем образце.
Стимуляция любого зонда для оптогенетики или фотостимуляции
Полигон обеспечивает большую гибкость при выборе длины волны. Polygon может проецировать свет разных цветов, от УФ до видимого/ближнего ИК-диапазона, подходящего для ваших светочувствительных конструкций.
Выберите градиентное освещение клетки, экспрессирующей новую оптогенетическую конструкцию, с помощью полигона (любезно предоставлено Эллиотом Дайном и доктором Джаредом Тетчером, Принстонский университет).
Пространственно-временной контроль и управление интенсивностью света
Управление началом, продолжительностью и интенсивностью световой стимуляции с помощью полигона. Создавайте различные формы волны, чтобы контролировать интенсивность и продолжительность света, выводимого из полигона.
УФ-фотошаблон (предоставлено Гайлой Берг, Колорадский университет).
УФ-микропаттерн с субмикронным разрешением
Polygon совместим с источниками УФ-излучения (350 нм+) и обеспечивает субмикронное освещение для экспериментов по фотопаттерну и микрообработке.
Интегрируется в любой электрофизиологический, двухфотонный или конфокальный микроскоп
Polygon предназначен для подключения к бесконечному пространству любой модели микроскопа (Leica, Nikon, Olympus, Zeiss) с адаптерами Mightex для конкретных микроскопов. Polygon оснащен триггерным входом и выходом TTL с разъемом BNC для легкой синхронизации с различным лабораторным оборудованием.
Polygon оснащен триггерным входом и выходом TTL с разъемом BNC для легкой синхронизации с различным лабораторным оборудованием.
Модели освещения с использованием полигона, синхронизированного с электрофизиологическими записями срезов (любезно предоставлено Мэтью Траном и доктором Блейком Ричардсом, Университет Макгилла).
Выберите освещение отдельных клеток, экспрессирующих ChR2, в срезе, используя Polygon (любезно предоставлено Мэтью Тран и доктором Блейком Ричардсом, Университет Макгилла).
Неврология Оптогенетика
Оптогенетика продвинула область нейробиологии, предоставив точный метод управления активностью нейронов. Возможность выполнять оптогенетику с клеточным разрешением позволяет исследователям стимулировать отдельные экспрессирующие оптогенез нейроны (например, ChR2, NpHr, Chrimson и т. д.) в срезе или культуре во время электрофизиологических записей или визуализации кальция для картирования нейронных цепей.
Соответствующие публикации с использованием полигона:
Kauver IV et al. (2020). Наблюдение за корой головного мозга с помощью синхронной мультифокальной оптической выборки выявляет широко распространенное популяционное кодирование действий. Нейрон.
Chong E et al. (2020). Манипуляции с синтетическими запахами раскрывают логику кодирования обонятельного восприятия. Наука.
Kissinger ST et al. (2020). Колебания, зависящие от визуального опыта, и основные изменения подключения схемы ухудшаются в Fmr1 KO Мыши. Отчеты сотовых.
Отчеты сотовых.
Грувер К.М. и Ватт А.Дж. (2019). Оптимизация оптогенетической активации аксонов клеток Пуркинье для исследования клетки Пуркинье — синапса DCN. Границы синаптической нейронауки .
Табор К.М. и др. (2018). Пресинаптическое торможение избирательно направляет слуховую передачу на цепь вздрагивания ствола мозга. Актуальная биология.
Андраси и др. (2017). Дифференциальное управление возбуждением двух параллельных корзинчатых клеточных сетей в микросхемах миндалевидного тела. ПЛОС Биология .
Клеточная биология Оптогенетика
Оптогенетические инструменты расширились, чтобы предложить клеточным биологам беспрецедентный пространственно-временной молекулярный и клеточный контроль. От миграции клеток до регуляции генов или процессов развития, клеточные биологи теперь имеют возможность с невероятной точностью вызывать специфические биологические реакции в конкретных клетках организмов или субклеточных областях отдельных клеток с помощью оптогенетики.
Выберите градиентное освещение клетки, экспрессирующей новую оптогенетическую конструкцию, с помощью полигона (любезно предоставлено Эллиотом Дайном и доктором Джаредом Тотчером, Принстонский университет).
Соответствующие публикации с использованием Polygon:
Johnson HE et al. (2020). Оптогенетическое спасение паттернирующего мутанта. Актуальная биология.
Дайн Э. и др. (2018). Разделение белковых фаз обеспечивает долговременную память о переходных пространственных стимулах. Клеточные системы.
ван Харен Дж. и др. (2018). Локальный контроль динамики внутриклеточных микротрубочек с помощью фотодиссоциации EB1. Природа Клеточная биология.
Johnson HE et al. (2017). Пространственно-временные ограничения передачи сигналов Erk в процессе развития. Развивающая ячейка.
Развивающая ячейка.
Адриан М. и др. (2017). Фотопереключатель на основе фитохрома для внутриклеточного транспорта. Синтетическая биология ACS.
Фотоактивация/фотоконверсия
Достижения в технологии флуоресцентных белков сделали методы фотоактивации широко доступными в лабораториях клеточной биологии. Используя эти методы, исследователи могут флуоресцентно выделять/маркировать определенные популяции белков в клетке, чтобы можно было отслеживать их движение и поведение с течением времени. Кроме того, методы фотоактивации могут применяться в различных масштабах, что позволяет исследователям отслеживать белки внутри клеток или, альтернативно, отслеживать клетки в тканях.
Соответствующие публикации с использованием полигона:
Tabor KM et al.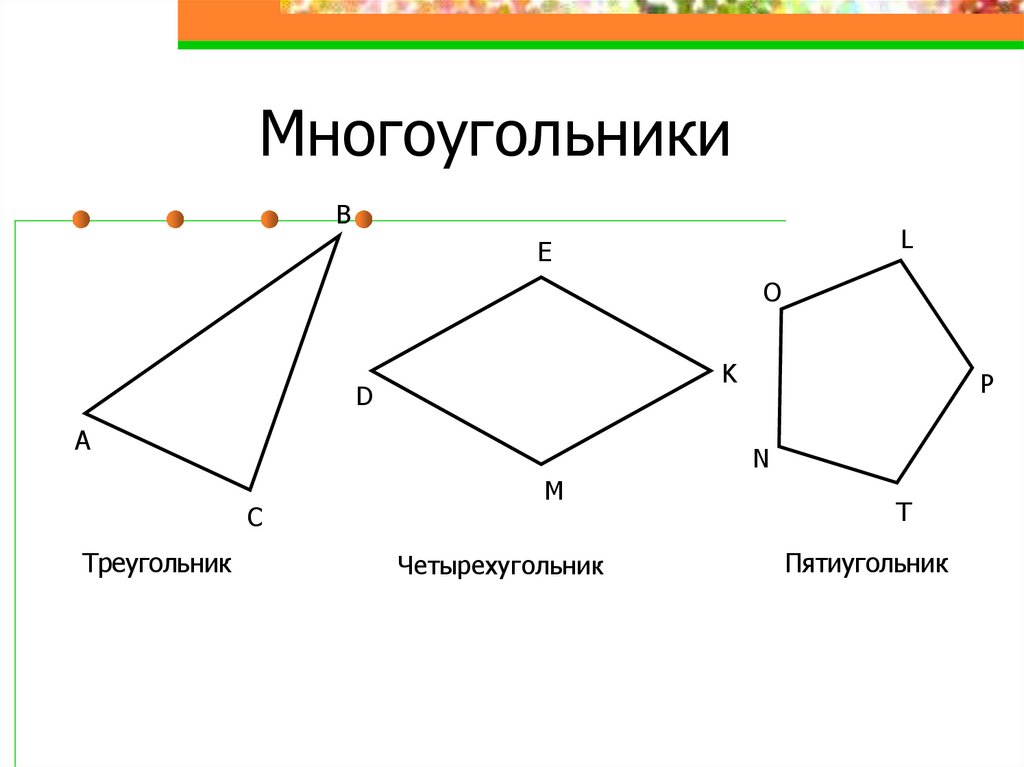 (2018). Пресинаптическое торможение избирательно направляет слуховую передачу на цепь вздрагивания ствола мозга. Актуальная биология.
(2018). Пресинаптическое торможение избирательно направляет слуховую передачу на цепь вздрагивания ствола мозга. Актуальная биология.
Осгасавара и др. (2018). Транскрипция, управляемая обратимым фотоконтролем гиперстабильных G-квадраплексов. Синтетическая биология ACS.
Создание фотошаблонов
Для управления различными свойствами клеточного микроокружения было разработано множество методов. Недавно появление светоиндуцированных биохимических соединений позволило ученым определить биохимические и структурные особенности клеточного матрикса с помощью фотомикроструктурирования и фотолитографии. Ученые могут точно определить пространственное распределение УФ-излучения для создания уникальной клеточной микросреды без использования масок или физического контакта с субстратом.
УФ-фотошаблон (любезно предоставлено Гайлой Берг, Университет Колорадо).
Соответствующие публикации с использованием полигона:
Geisterfer ZM et al. (2020). Скорость роста микротрубочек чувствительна к глобальным и локальным изменениям плотности плюс-конца микротрубочек. Актуальная биология.
(2020). Скорость роста микротрубочек чувствительна к глобальным и локальным изменениям плотности плюс-конца микротрубочек. Актуальная биология.
Fattahi N et al. (2020). Фоторазлагаемые гидрогели для быстрого скрининга, выделения и генетической характеристики бактерий с редкими фенотипами. Биомакромолекулы .
Норен Б.Е. и др. (2019). Клеточная печать в сложных гидрогелевых каркасах. Транзакции IEEE по нанобиологии.
ван дер Влис А.Дж. и др. (2019). Высвобождение по требованию и извлечение бактерий из микролуночных матриц с использованием фоторазлагаемых гидрогелевых мембран. Прикладные биоматериалы ACS.
Оптоэлектронный пинцет для перемещения определенных клеток (любезно предоставлено доктором Шуайлун Чжаном, Университет Торонто).
Микрофлюидика
Микрофлюидные устройства изготавливаются путем нанесения тонкопленочных материалов-предшественников на подложку с фотоструктурированием для создания микроскопических каналов, камер и даже механизмов управления потоком. Небольшие количества жидкостей, содержащих реакционноспособные химикаты или другие вещества, могут затем проходить через микроканалы и смешиваться в микрокамерах устройства и вступать в реакцию с другими веществами, которые могут осаждаться в микроканалах.
Небольшие количества жидкостей, содержащих реакционноспособные химикаты или другие вещества, могут затем проходить через микроканалы и смешиваться в микрокамерах устройства и вступать в реакцию с другими веществами, которые могут осаждаться в микроканалах.
Модели
Различные модели, оптимизированные для медико-биологических приложений
Различные модели, оптимизированные для медико-биологических приложений
Mightex предлагает несколько моделей Polygon, которые были разработаны с различными функциями для удовлетворения потребностей широкого спектра приложений, использующих шаблоны. освещение. Пожалуйста, смотрите ниже все доступные модели Polygon.
Polygon1000-G
Polygon1000-G — это гибкое решение для направленного освещения, поскольку этот узорчатый осветитель можно использовать с любым источником света (350–700 нм), который принимает световод с сердечником диаметром 3 мм. Таким образом, Polygon1000-G обеспечивает будущую гибкость для различных длин волн и источников света, в зависимости от вашего приложения.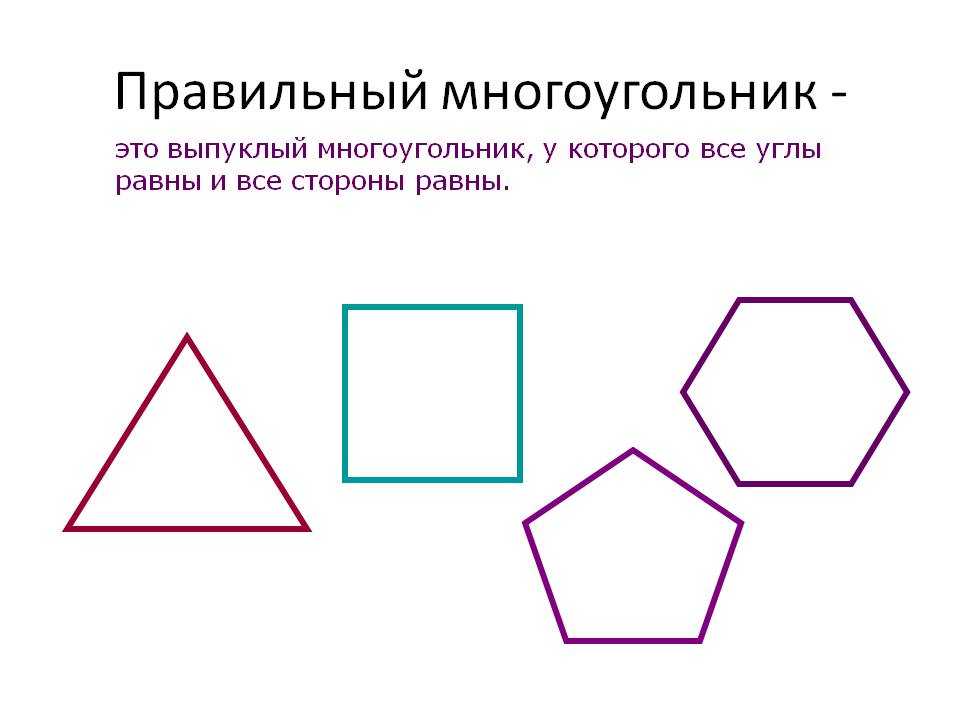
- Длина волны: 350–700 нм
- Источник света: со световодом
- Дополнительная передняя трубка для большого поля зрения
Polygon1000-DL
Polygon1000- DL — это гибкое решение для большого поля зрения или применения в высокомощном узорчатом освещении, так как этот узорчатый осветитель можно использовать с любым оптоволоконным источником света (400–700 нм), например, с мощными лазерами. Эта модель Polygon1000 была разработана для высокопроизводительных приложений, таких как оптогенетика in vivo.
- Длина волны: 400–700 нм
- Источник света: оптоволоконный
Polygon1000-G (стандартный)
Polygon1000-G (большое поле зрения)
904 09 Polygon400-G* Polygon400-G гибкое решение для узорчатого освещения, поскольку этот узорчатый осветитель можно использовать с любым источником света (400-700 нм), который принимает световод с сердцевиной 3 мм. Таким образом, Polygon400-G обеспечивает будущую гибкость для различных длин волн и источников света, в зависимости от вашего приложения.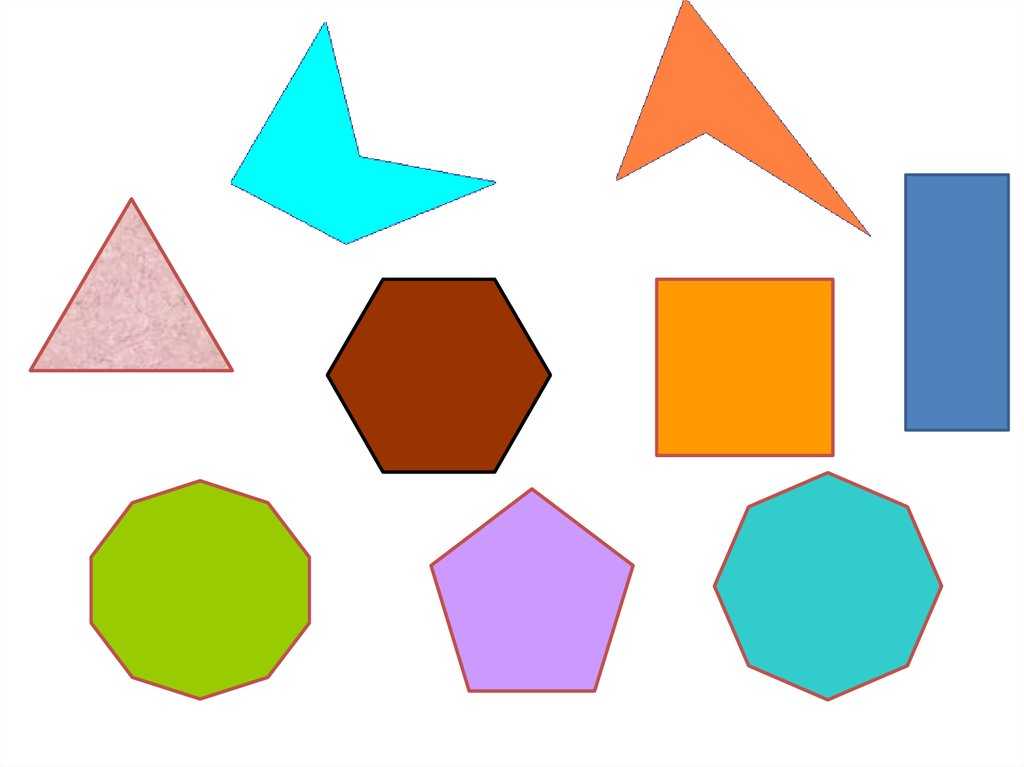
- Длина волны: 400-700 нм
- Источник света: со световодом
*Снято с производства. Заменена серией Polygon1000.
Ресурсы
Вебинары
Белая книга/Примечания по применению
Свяжитесь с нами
600+ лабораторий по всему миру, более 100 публикаций с использованием Polygon
Mightex Ведущий на рынке осветитель модели Polygon DMD обеспечивает точное пространственно-временное управление светом с субклеточным разрешением. , что делает его идеальным инструментом освещения для исследований в области наук о жизни.
Оптогенетика клеточного разрешения и фотостимуляция
Одновременное многозональное освещение
Субклеточное разрешение
9 0013
Совместим с любым микроскопом
Брошюра и технические характеристики Polygon
Art Illumination Technology
Polygon использует технологию цифрового зеркального устройства (DMD) для одновременного освещения нескольких областей. DMD состоит из сотен тысяч микрозеркал, которые можно включать по отдельности, чтобы отражать свет на образец. Таким образом, вы можете управлять каждым зеркалом, чтобы управлять областью (областями) освещения и создавать любое количество узоров разного размера. Осветитель полигона Polygon DMD можно установить на бесконечном пути любого микроскопа.
DMD состоит из сотен тысяч микрозеркал, которые можно включать по отдельности, чтобы отражать свет на образец. Таким образом, вы можете управлять каждым зеркалом, чтобы управлять областью (областями) освещения и создавать любое количество узоров разного размера. Осветитель полигона Polygon DMD можно установить на бесконечном пути любого микроскопа.
Основные характеристики многоугольника
Одновременная оптогенетическая стимуляция отдельных клеток или субклеточных компонентов
Выберите освещение отдельных клеток, экспрессирующих ChR2, в срезе с использованием многоугольника (любезно предоставлено Мэтью Траном и доктором Блейком Ричардсом, Университет Макгилла).
Многоугольник позволяет ученым точно контролировать, где свет будет падать на их образец. С субклеточным разрешением Polygon может одновременно освещать любые клеточные элементы любой формы и размера на своем образце.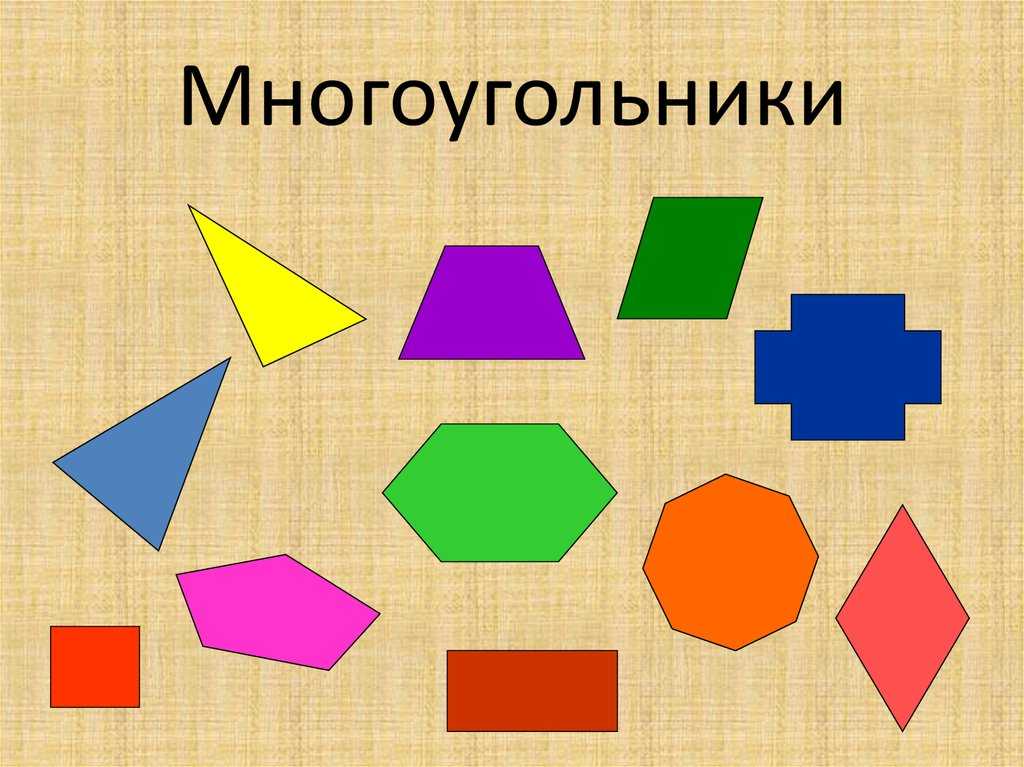
Стимуляция любого зонда для оптогенетики или фотостимуляции
Полигон обеспечивает большую гибкость при выборе длины волны. Polygon может проецировать свет разных цветов, от УФ до видимого/ближнего ИК-диапазона, подходящего для ваших светочувствительных конструкций.
Пространственно-временной контроль и управление интенсивностью света
Выберите градиентное освещение клетки, экспрессирующей новую оптогенетическую конструкцию, с помощью полигона (любезно предоставлено Эллиотом Дайном и доктором Джаредом Тотчером, Принстонский университет).
Контролируйте начало, продолжительность и интенсивность световой стимуляции с помощью полигона. Создавайте различные формы волны, чтобы контролировать интенсивность и продолжительность света, выводимого из полигона.
УФ-микроструктурирование с субмикронным разрешением
УФ-фотоструктурирование (любезно предоставлено Гайлой Берг, Университет Колорадо).
Polygon совместим с источниками УФ-излучения (350 нм+) и обеспечивает субмикронное освещение для экспериментов по фотопаттерну и микрообработке.
Интегрируется в любую установку электрофизиологического, двухфотонного или конфокального микроскопа
Модели освещения с использованием полигона, синхронизированного с электрофизиологическими записями срезов (любезно предоставлено Мэтью Траном и доктором Блейком Ричардсом, Университет Макгилла).
Polygon предназначен для подключения к бесконечному пространству любой модели микроскопа (Leica, Nikon, Olympus, Zeiss) с помощью адаптеров Mightex для конкретных микроскопов.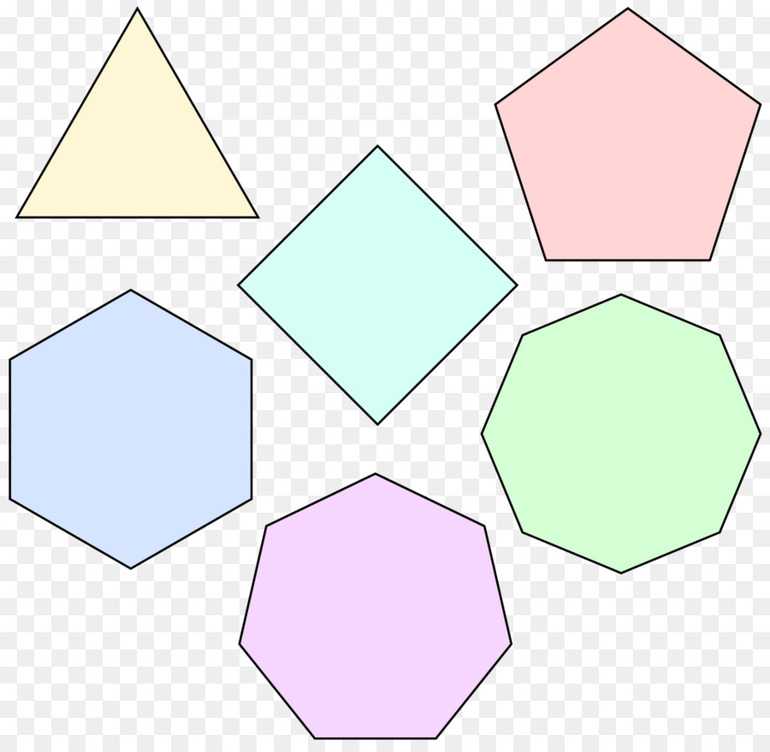
 Автор — Попов М.А. — 2013 год
Автор — Попов М.А. — 2013 год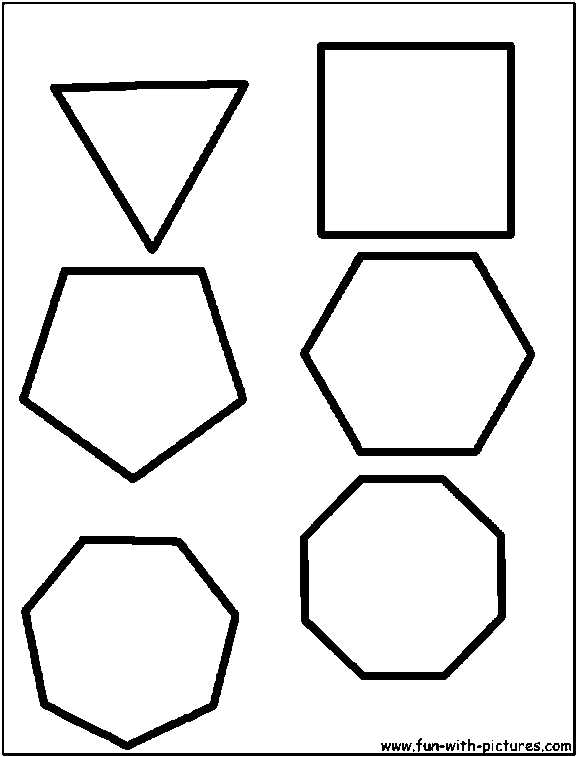 Б., Прасолов В.В. Геометрия, 8 класс. — М.: Просвещение, 2011.
Б., Прасолов В.В. Геометрия, 8 класс. — М.: Просвещение, 2011.