Воображаемая ось и настоящая: У юлы настоящая или воображаемая ось вращения?

У телеги настоящая, у Земли воображаемая, 3 буквы, первая буква О — кроссворды и сканворды

ось

Слово «ось» состоит из 3 букв:

— первая буква О

— вторая буква С

— третья буква Ь

Посмотреть значние слова «ось» в словаре.

Альтернативные варианты определений к слову «ось», всего найдено — 52 варианта:

• «БерлинРимТокио»
• «Стержень» Земли
• «Трутся об … медведи»
• «Трутся спиной медведи о земную …»
• … абсцисс
• … ординат
• OX
• «Аксон» в переводе с греческого
• «Терка» для спин медведей
• Вокруг нее вращаются
• Вокруг нее колесо крутится
• Воображаемая линия, вокруг которой вращается тело
• Воображаемая прямая линия
• Гитлеровская коалиция
• Деталь механизма
• Единственная неподвиж. часть колеса
• Ее в песне вертят белые медведи
• Земная …
• Земной «стержень»
• Линия вращения
• Линия координат в математике
• Линия симметрии
• Между двух полюсов
• Местоим. стар. сей? малорос. вот, здесь, тут. Улюби же король Андрей совет ось (сего, вот этого) Пакослава, стар
• На неё насаживают колесо
• На чем вращается обод
• Опора балансира
• Оптическая … кристалла
• Ордината или абсцисса
• ОХ
• Палка в глобусе
• Палка от полюса до полюса
• Прямая координат
• Рим-Берлин-Токио
• Союз государств
• Стержень
• Стержень в колесе
• Стержень в центре колеса
• Стержень, на котором держатся колеса
• Стержень, на который «насажена» Земля
• Сущ. ж. см. острить
• То, на чем крутится колесо и Земля
• Тоньше, чем вал
• У Земли она одна, а у теле-…
• Центр вращения
• Центр симметрии
• Центральная часть колеса
• Центральный стержень вращения
• Часть Земли, о которую «трутся спиной медведи», отчего она и вертится
• Шпиндель как деталь
• Штуковина, о которую трутся медведи
• Штырь, с помощью которого прицельно-спусковое устройство крепится к ложе

Другие вопросы:

• Домашний гибрид баньки и бассейна
• Громкость звучания в музыке
• Озёрное шотландское чудище
• Российский лётчик-испытатель
• Разновидность мягкой пшеницы
• Растение семейства розоцветных, медоносное, декоративное, сорняк (таволга)
• Оборудование на сцене
• Почтительный поклон с приседанием
• Платформа Рижского направления
• Отец Екатерины Арагонской

Только что искали: пафромор сейчас м о д е л ь сейчас бросок сейчас к а н л а и сейчас н и л а б ы т сейчас арнаутле сейчас д е с п о т сейчас я ш е у в да сейчас с к о о д о т в 1 секунда назад нсоез 1 секунда назад онсткарт 1 секунда назад ьпанепка 1 секунда назад с р т а ж а 1 секунда назад т е с а к 1 секунда назад с в а л к а 1 секунда назад

Конспект урока «Земля.

Модель земли»

Урок окружающего мира во 2 «Г» классе

Учитель: Рябинина Ольга Владимировна

УМК «Перспективная начальная школа»

Тема: Земля. Модель земли.

Цель урока: создание условий для формирования метапредметных умений средствами урока «окружающий мир»

Задачи урока:

• Уточнить детские представления о Солнце и Земле,

• Обсудить, что представляет собой глобус (уменьшенная модель Земли).

• Познакомить с новыми понятиями: «модель» «воображаемая ось», «экватор», «Северное и Южное полушария», «Северный и Южный полюс».

• Научить находить на глобусе Северный полюс, Южный полюс, Северное полушарие, Южное полушарие, экватор;

• Формировать умение работать с глобусом и навык устного составления рассказа.

• Формировать коммуникативную компетенцию: умение вести диалог, координировать свои действия с действиями партнера по совместной деятельности.

• Развивать самостоятельность мышления, познавательный интерес к окружающему миру.

Планируемые результаты

Предметные: уметь объяснять значение терминов «экватор»,»полюса», «полушария» ,находить на глобусе Северный и Южный полюса, Северное и Южное полушария.

Метапредметные:

Коммуникативные: навыки делового партнёрского общения; умения находить и исправлять ошибки в работе соседа и при коллективном обсуждении.

Регулятивные:

Рефлексивные умения: осмыслить практическую задачу, для решения которой недостаточно имеющихся знаний.

Оценочные умения: сравнивать полученные результаты с поставленной задачей; оценивать свою деятельность на уроке, определять успехи и трудности.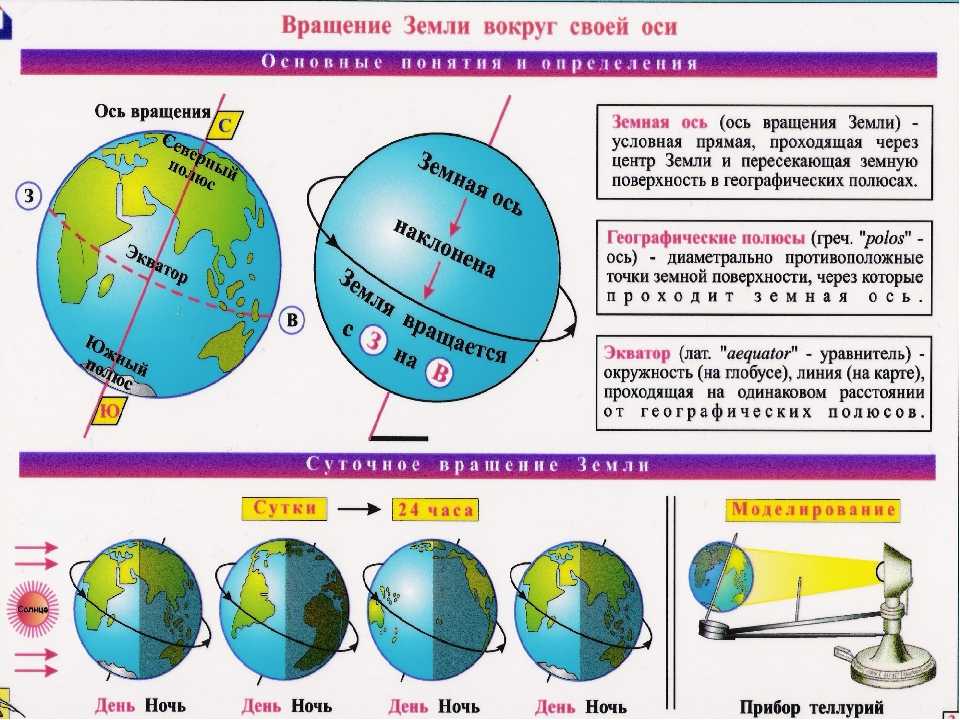

Познавательные:

Общеучебные действия: умение строить речевое высказывание в устной форме по вопросам; извлекать необходимую информацию из текста

Логические действия: умение строить логическую цепь рассуждений

Личностные: формирование позитивной самооценки.

Оборудование и наглядные пособия: учебники, тетради для самостоятельной работы, демонстрационный глобус, интерактивная доска, карточки с опорными словами (модель, экватор, Северный полюс, Южный полюс, Северное полушарие, Южное полушарие, воображаемая ось), красный и синий карандаши, зубочистки , карточки с тестом.

Ход урока:

1.Самоопределение к учебной деятельности

— Какой у нас сейчас урок? (окружающий мир)

— Что дает нам этот предмет? (новые знания об окружающем мире)

— Для чего нужны знания?

2. Актуализация знаний

—Отгадайте, загадку:

Сколько ни езди, ни ходи,

Тебе конца тут не найти. (земля)

-Что вы знаете о Земле?

-Что обозначает слово «земля», когда оно записано с маленькой буквы? (земля-почва)

— А с большой? (Земля-это планета).

-А какой формы нашла планета Земля? (шар)

-(СЛАЙД 1)Оказывается, давным-давно люди были уверены, что Земля – плоский круг среди безграничного океана. В Индии считали, что Землю держат 4 слона, а слоны стоят на громадной черепахе.

-(СЛАЙД 2)Древние греки считали, что Земля – медный диск, который омывается

со всех сторон океаном. Над Землей раскинулся небосвод, по которому

движется Солнце, поднимаясь и погружаясь ежедневно в воды океана.

-(СЛАЙД 3) А вот так видят нашу Землю космонавты из космоса.

-Какая звезда самая близкая к планете Земля? (Солнце)

-Что вы знаете о Солнце? (Солнце – огромный раскаленный светящийся шар)

-Каким вы видите Солнце? (Маленьким кружком)

-Земля от Солнца очень далеко, около 150 млн км. Свет Солнца преодолевает это расстояние за

8 минут, он летит со скоростью 300000 км в секунду.

Посмотрим видеоролик о Солнце

http://www.youtube.com/watch?v=hCHwcnYVGhg

-Достаточно у вас знаний об этих объектах природы?

Хотите узнать о них больше?

-Какие главные источники информации нам помогут получить новые знания?

(учебник, рабочая тетрадь)

3. Постановка цели урока

-Откройте оглавление учебника «Окружающий мир».

— Назовите следующую тему урока. («Земля-модель Земли)

-На какой странице она находится? (стр. 17)

-Какую цель поставим на урок? (Узнать, что такое модель Земли)

-Мы познакомимся с моделью Земли, узнаем, что находится на этой модели и как она выглядит.

-Какой видят космонавты Землю из космоса? (голубой, шарообразной).

-Какие цвета есть на нашей планете? (голубой, белый, синий, коричневый)

-Что обозначает каждый цвет? (Голубой и синий — моря, океаны, озёра; коричневый — суша, белый-облака)

-Чего на Земле больше: суши или воды? (Воды)

-Почему на снимке из космоса наша планета голубая? (Вода занимает больше половины земного шара)

4.Формирование новых знаний

-Иногда, чтобы изучить какой-либо предмет, учёные делают его уменьшенное или увеличенное изображение – модель.

-Откройте учебник на стр. 18.

-Рассмотрите на рисунке пожарную машину и её модель.

-Чем они отличаются?

-Ребята! Что такое модель? Где мы можем найти эту информацию? (В словаре)

-Найдите и прочитайте. (Модель-предмет, сделанный человеком. Уменьшенная модель Земли – глобус, повторяет её форму, но отличается размером)

Отгадайте загадку:

На ноге стоит одной,

Крутит, вертит головой.

Нам показывает страны,

Реки, горы, океаны.

(Глобус)

Глобус — это модель земного шара. (Показать глобус)

—Найдите и покажите изображение глобуса соседу по парте на стр.19.

-Почему он получил такое название?

(СЛАЙД 4) Глобус в переводе с лат.яз. – шар. Первый глобус появился более 500 лет назад, в Германии, создал его немецкий географ Мартин Бехайм. Сделал он из телячьей кожи, туго натянутой на металлические ребра. Он назвал свою модель «земное яблоко». До сих пор первый глобус хранится в одном из музеев Германии.  

-Давайте понаблюдаем за глобусом.

-Что показывают цвета глобуса? (где поверхность Земли покрыта водой, где на ней суша, горы).

Повращаем его. Земля вращается. Поэтому вращается и глобус.

-Что помогает нам вращать глобус? ( стержень)

-Стержень-это ось вращения. У глобуса ось вращения настоящая, а у Земли?

-Обратите внимание, глобус немного наклонён. Почему его наклонили?

(В таком положении Земля вращается вокруг воображаемой оси).

Работа в тетради на печатной основе, зад. 8, стр. 6

— Назовите предметы. На каждый предмет по направлению оси вращения положите зубочистку.

— Назовите те предметы, у которых мы видим ось вращения. (глобус, юла, винт вертолета). У этих предметов настоящая ось вращения.

— Синим карандашом проведите настоящую ось вращения.

-У каких предметов мы ось не видим, а представляем (воображаем)?

(балерина, вихрь, Земля)

-Такая ось называется воображаемая ось вращения.

-Проведите красным карандашом воображаемую ось.

-Какая ось у планеты Земля — настоящая или воображаемая?

Физминутка

Вы, наверное, устали? Ну, тогда все дружно встали!

http://pedsovet.su/load/244-1-0-34315

-Как называются точки на глобусе, через которые проходит ось вращения? (Северный и Южный полюсы)

-Выйдите к доске и покажите на глобусе Северный и Южный полюсы.

(Ученик прикрепляет табличку «Северный полюс», «Южный полюс»)

-Посмотрите на толстую линию на глобусе, которая делит нашу планету на 2 полушария Северное и Южное.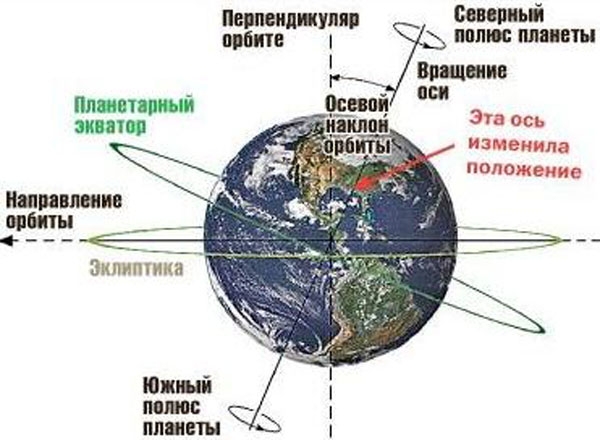 Как она называется? (экватор)

( 1 ученик прикрепляет табличку «Экватор» на глобус)

-Кто покажет, где находится наша страна? В каком полушарии мы живем? (Северном).

На глобусе есть еще и горизонтальные и вертикальные линии.

-Линии, которые идут с севера на юг, называются меридианы.

-Линии, которые идут с запада на восток, называются параллели.

— Поэтому иногда глобус называют «мяч в сетке».

5.Закрепление изученного материала

Работа в паре

-Давайте вспомним правила работы в паре.

1.Чётко высказывай своё мнение.

2. Умей слушать товарища.

3. Если не согласен с мнением товарища:

не кричи, не перебивай, пользуйся вежливыми словами.

4. Не смейся над чужими ошибками.

У вас на парте лежит лист с тестом.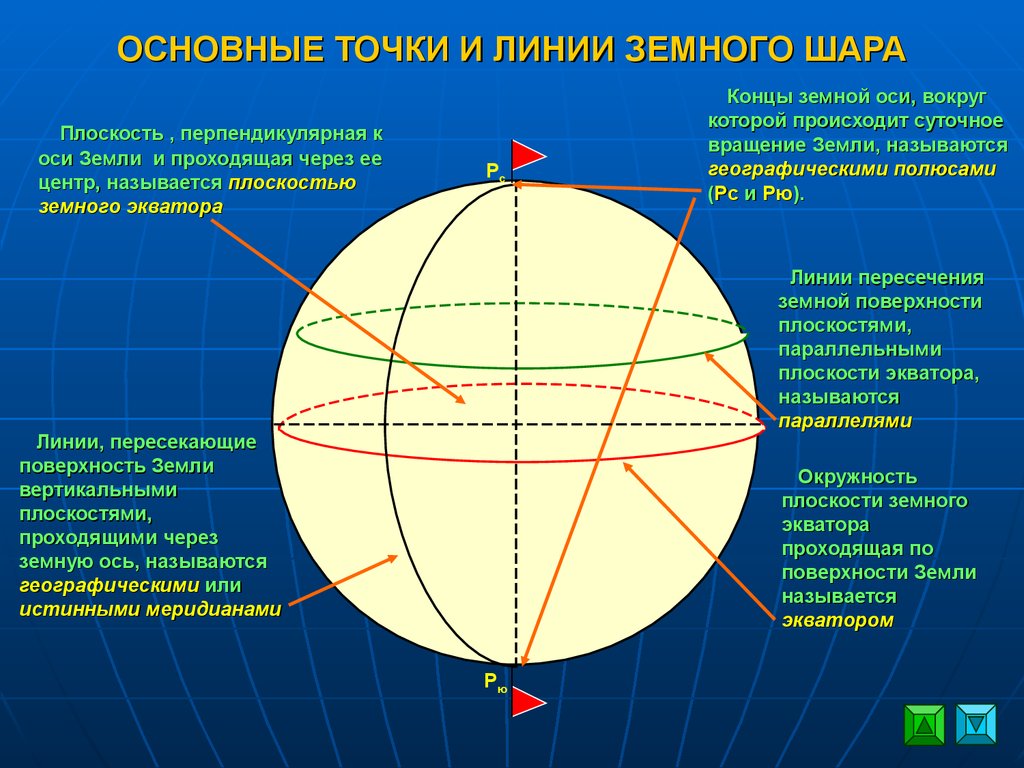 Выполните его в паре. Приложение 1

-Какую цель мы ставили в начале урока? (узнать, что такое модель Земли)

Узнали? Что же такое глобус?

-Попробуем сформулировать, что же такое глобус.

(Глобус—модель Земли в форме шара, который разделен экватором на два полушария –Северное и Южное.)

-Давайте сравним наши предположения с определением из словаря.

-Достигли ли мы цели урока? (Да)

Рефлексия учебной деятельности

— Оцените себя:

Если всё поняли и довольны собой, покажите – зелёный кружок.

Если испытывали затруднения, покажите – жёлтый кружок.

Если вам было очень трудно, не интересно, покажите – красный кружок.

Домашнее задание

Стр.17-19 вопросы, вылепить из пластилина модель Земли .Тетрадь с.5 №7.

комплексных чисел. Почему на диаграмме Аргана существует воображаемая ось?

спросил

5 лет, 8 месяцев назад

Изменено 5 лет, 3 месяца назад

Просмотрено 1к раз

$\begingroup$

Комплексные числа могут немного озадачить меня, и я думаю, что у меня есть некоторые пробелы в моем понимании, из-за которых мне трудно обернуть голову.

Вот как я пытаюсь объяснить себе комплексные числа:

• Если мы не включаем комплексные числа, мы можем найти числа, которые не могут существовать на декартовой плоскости, например, с комплексными решениями некоторых квадратичных уравнений. У нас есть пропущенных чисел на нашей декартовой плоскости, и мы пытаемся представить все числа на этой плоскости.
• Если вместо этого мы представим все числа как $a + bi$ вместо $a$, мы сможем идентифицировать все числа и выразить их на декартовой плоскости.

Если моя интерпретация в чем-то неверна, пожалуйста, объясните, почему.

Тем не менее, мой главный вопрос заключается в том, почему из этого следует, что теперь у нас есть производная диаграммы Аргана от декартовой плоскости, состоящей только из вещественных чисел, с мнимой осью на оси $y$ и вещественными числами на оси $x$? Связано ли это с логическим продолжением того, что я сказал: «Если мы вместо этого представим все числа как $a + bi$ вместо $a$, то теперь мы сможем идентифицировать все числа и выразить их на декартовой плоскости»? Уточню:

• Поскольку числа теперь выражаются в форме $a + bi$, если воображаемая ось проходит по оси $y$, а прямая с действительными числами проходит по оси $x$, все числа могут быть учтены элегантно.
• Это связано с тем, что теперь любое число можно выразить его проекцией на мнимую и действительную оси.

Но благодаря тому, что кто-то установил это правило, теперь у нас есть следующие свойства:

• Теперь мы используем векторы для типизации чисел. $3 + 2i$ теперь является проекцией на эту плоскость, и теперь мы используем такие вещи, как сложение векторов. И тогда это может снежным комом превратиться в тождество Эйлера?!
• Умножение на $i$ теперь заставляет проекции «вращаться» в плоскости.

Мне это кажется странным, потому что мы решили определить нашу ось $y$ как число, умноженное на квадратный корень из $-1$, что звучит совершенно произвольно.

Почему я не мог сделать свою собственную диаграмму и вместо того, чтобы умножать числа по оси Y на $i$, я умножал их на $k$, которые я определяю как равные $13$? И все эти новые свойства, которые я перечислил, такие как расширенная декартова плоскость, которая теперь является чем-то вроде векторного пространства и имеет свойства вращения, кажутся мне безумием.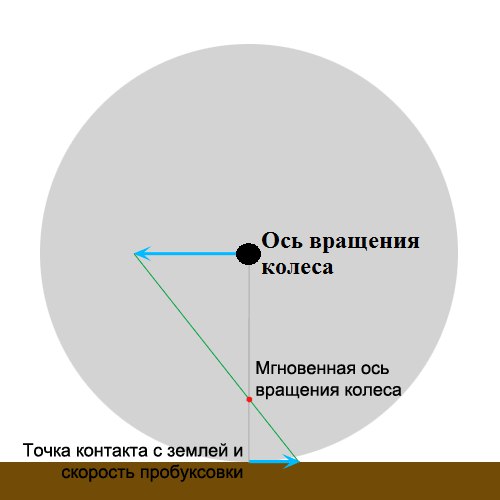

— $$ \bbox[2px,border:2px сплошной красный] { Итак,\ чтобы\ резюмировать,\ мой\ главный\ вопрос\ состоит в следующем:\ почему\ все\ это\ было\ реализовано*,\ имея\ в памяти\ новые\ странные\ свойства\ наши\ расширенные\ картезианские \ самолет\ сейчас\ есть?\ } $$

Что во всем этом такого? Как и почему мы ушли от нашего числового ряда реалов и пришли ко всему этому?

Надеюсь, я достаточно ясно изложил свой вопрос. Пожалуйста, дайте мне знать, если что-то нужно сделать более ясным.

* И под «все это было реализовано» я имею в виду создание оси $y$, воображаемой оси, для прямой числовой линии и обеспечение возможности формирования всех этих странных свойств, отсюда и название. 92$ и свяжем каждой точке $(x,y)$ число $x+13k$. Хотя проблема с , что конкретный план

, заключается в том, что каждое число теперь представляет много разных точек — например, $(13,0)$ и $(0,1)$ и $(26,-1)$ теперь все связано с числом $13$. Это означает, что мы не можем использовать схему ни для чего, где мы вычисляем число, и это число указывает ровно на одну точку на плоскости. 2$ в виде $x+\alpha y$.

Как и в случае с $13$, если мы выберем $\alpha\in\mathbb R$, то получим что-то, где число не представляет уникальную точку. Предположим, однако, что мы избегаем этого случая, и, кроме того, мы оказываемся в счастливой ситуации, когда каждый элемент поля представляет некоторые $(x,y)$ на плоскости.

Тогда происходит что-то чудесное, а именно, мы можем доказать (хотя и не в оставленном мне месте на этом поле), что поле, которое мы используем, должно быть изоморфно $\mathbb C$ — другими словами, поле

— это, по сути, комплексные числа, просто называемые по-другому. В частности, где-то на плоскости есть $(x,y)$, соответствующее число которого ведет себя точно так же, как $i$.

Таким образом, мы могли бы сказать: возьмем некоторое комплексное число $\alpha$, и пусть $(x,y)$ соответствует $x+\alpha y$. Пока $\alpha$ не реально, это даст нам идеальное взаимно однозначное соответствие между точками и комплексными числами.

Теперь среди всех возможных вариантов $\alpha$ оказывается, что именно при $\alpha=i$ или $\alpha=-i$ мы получаем дополнительное приятное свойство, состоящее в том, что умножение на любое фиксированное ненулевое комплексное число будет соответствовать преобразованию плоскости, переводящему геометрические фигуры в подобных геометрических фигур.

Наличие умножения, соответствующего преобразованиям подобия, является довольно изящным свойством, которое является причиной предпочтения представления $x+iy$ другим возможным $x+\alpha y$.

$\endgroup$

2

$\begingroup$

Я думаю, ваши трудности начинаются здесь:

Если мы не включаем комплексные числа, мы можем найти числа, которые не могут существовать на декартовой плоскости, например, с комплексными решениями некоторых квадратичных уравнений. Нам не хватает чисел на нашей декартовой плоскости, и мы пытаемся представить все числа на этой плоскости.

92 + 1 = 0,$, для которого каждое решение состоит всего из одного числа, не пара цифр.

На самом деле причина изобретения комплексных чисел не имела ничего общего с декартовой плоскостью; потребовались сотни лет, чтобы эти две математические идеи вообще соединились. Кардано уже использовал $\sqrt{-1}$ как свой «странный трюк» для решения кубических уравнений в 1545 году. Декарт опубликовал свое представление о координатах плоскости в 1637 г. — уже почти столетие спустя! — а Арган впервые опубликовал свои диаграммы в 1806 г. 92 + 1 = 0.$ Поначалу математики неохотно принимали случайные комплексные числа в математике, потому что они могли использовать их, работая над проблемой нахождения

действительных решений уравнений кубической и четвертой степени. Полное признание комплексных чисел пришло намного позже.

В любом случае диаграммы Аргана возникли не потому, что Арган (или кто-то другой) сидел без дела, пытаясь придумать странные свойства, которые можно добавить к декартовой плоскости, и придумал это. Они возникли из-за того, что геометрическая интерпретация сложных операций на диаграмме Аргана точно соответствует тому, что уже было известно о комплексных числах; все эти свойства были доказаны алгеброй без каких-либо геометрических рассуждений.

$\endgroup$

Выражение и построение комплексных чисел

Результаты обучения

• Выражение квадратных корней из отрицательных чисел как кратных [latex]i[/latex] .
• Нанесение комплексных чисел на комплексную плоскость.

Мы знаем, как найти квадратный корень из любого положительного действительного числа. Аналогичным образом мы можем найти квадратный корень из отрицательного числа. Отличие в том, что рут не настоящий. Если значение подкоренной черты отрицательное, говорят, что корень равен 9.{2}=-1[/latex]

Мы можем записать квадратный корень из любого отрицательного числа как кратное [latex]i[/latex]. Возьмем квадратный корень из –25.

[латекс]\begin{align}\sqrt{-25}&=\sqrt{25\cdot \left(-1\right)}\\&=\sqrt{25}\cdot\sqrt{-1} \\ &=5i\end{align}[/latex]

Мы используем [latex]5i[/latex]   , а не [latex]-\text{5}i[/latex] , поскольку главный корень числа 25 является положительным корнем.

Комплексное число представляет собой сумму действительного числа и мнимого числа. Комплексное число выражается в стандартной форме, когда пишется [латекс]а+би[/латекс], где [латекс]а[/латекс] – действительная часть, а [латекс]би[/латекс] – мнимая часть. Например, [латекс]5+2i[/латекс] — это комплексное число. Так же и [латекс]3+4\sqrt{3}i[/латекс].

Мнимые числа отличаются от действительных чисел, поскольку возведение в квадрат мнимого числа дает отрицательное действительное число. Вспомните, когда возводится в квадрат положительное действительное число, результатом является положительное действительное число, а когда возводится в квадрат отрицательное действительное число, снова получается положительное действительное число. Комплексные числа представляют собой комбинацию действительных и мнимых чисел.

A Общее примечание: мнимые и комплексные числа

Комплексное число — это число в форме [латекс]а+би[/латекс], где

• [латекс]а[/латекс] — действительная часть комплексного числа.
• [латекс]би[/латекс] — мнимая часть комплексного числа.

Если [латекс]b=0[/латекс], то [латекс]а+би[/латекс] — действительное число. Если [latex]a=0[/latex] и [latex]b[/latex] не равен 0, комплексное число называется мнимым числом . Мнимое число – это четный корень из отрицательного числа.

Как: Задать мнимое число, представить его в стандартной форме.

1. Напишите [латекс]\sqrt{-a}[/латекс] как [латекс]\sqrt{a}\cdot\sqrt{-1}[/латекс].
2. Выразите [латекс]\sqrt{-1}[/латекс] как i .
3. Напишите [латекс]\sqrt{a}\cdot i[/латекс] в простейшей форме.

Пример. Выражение мнимого числа в стандартной форме

Выразите [латекс]\sqrt{-9}[/латекс] в стандартной форме.

Показать решение

Попробуйте

Экспресс [латекс]\sqrt{-24}[/латекс] в стандартной форме.

Показать решение

Нанесение комплексных чисел на комплексную плоскость

Мы не можем наносить комплексные числа на числовую прямую, как настоящие числа. Однако мы все еще можем представить их графически. Чтобы представить комплексное число, нам нужно обратиться к двум компонентам числа. Мы используем комплексную плоскость , которая представляет собой систему координат, в которой горизонтальная ось представляет действительную составляющую, а вертикальная ось представляет мнимую составляющую. Комплексные числа — это точки на плоскости, выраженные в виде упорядоченных пар [латекс](а, b)[/латекс], где [латекс]а[/латекс] представляет собой координату горизонтальной оси, а [латекс]b[/латекс ] представляет координату вертикальной оси.

Рассмотрим число [латекс]-2+3i[/латекс]. Действительная часть комплексного числа – [латекс]–2[/латекс], а мнимая часть – [латекс]3i[/латекс]. Мы наносим упорядоченную пару [латекс]\влево(-2,3\вправо)[/латекс] для представления комплексного числа [латекс]-2+3i[/латекс] .

A Общее примечание: комплексная плоскость

В комплексной плоскости горизонтальная ось является реальной осью, а вертикальная ось — мнимой осью.

Как: Для заданного комплексного числа представить его компоненты на комплексной плоскости.

1. Определите действительную и мнимую части комплексного числа.
2. Перемещайтесь по горизонтальной оси, чтобы показать действительную часть числа.
3. Перемещение параллельно вертикальной оси для отображения мнимой части числа.
4. Поставьте точку.

Пример: построение комплексного числа на комплексной плоскости

Нанесение комплексного числа [латекс]3 — 4i[/латекс] на комплексную плоскость.