Многоугольник рисунок: стороны, вершины, диагонали. Периметр многоугольника

Многоугольник

Определение 1. Многоугольник − замкнутая ломаная линия.

Объединение многоугольника и ограниченной им части плоскости также называют многоугольником. Поэтому представим другое определение многоугольника:

Определение 2. Многоугольник − это геометрическая фигура, которая является частю плоскости, ограниченная замкнутой ломаной.

Вершины ломаной называются вершинами многоугольника. Звенья ломаной называются сторонами многоугольника.

Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней областью многоугольника, а другая внешней областью многоугольника.

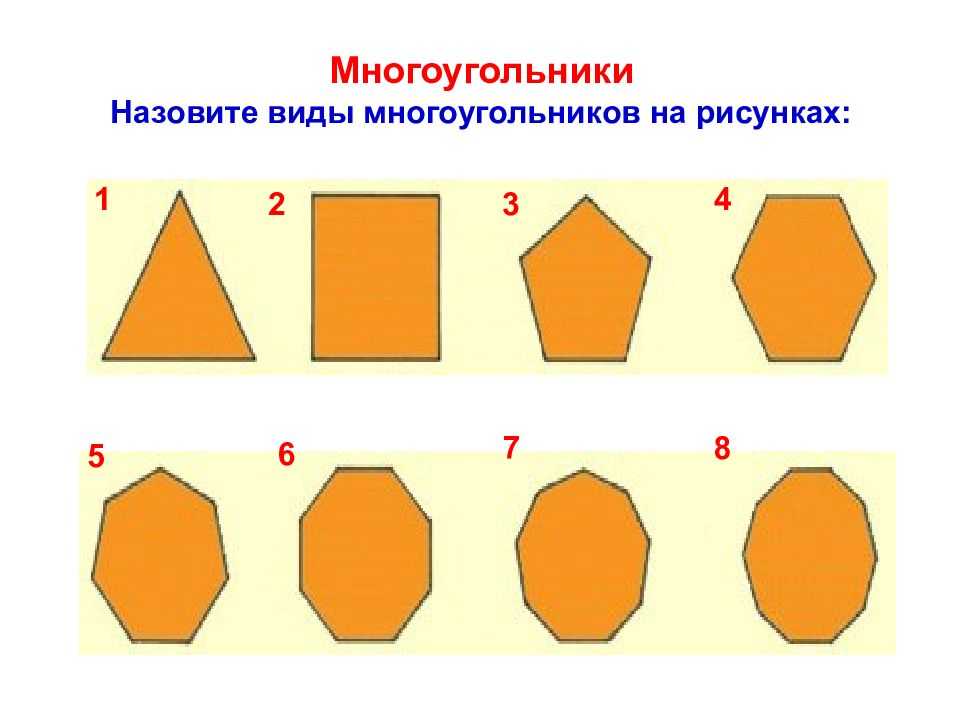
Виды многоугольников

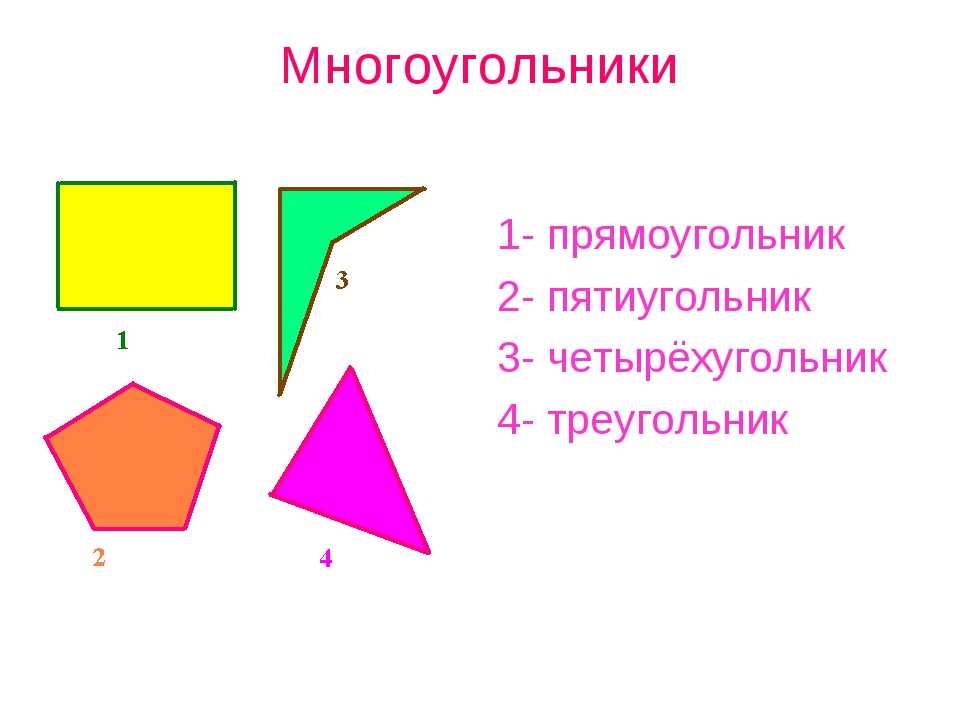
Многоугольник с тремя вершинами называется треугольником, с четыремя вершинами − четырехугольником, с пяти вершинами − пятиугольником, и т.д. Многоугольник с \( \small n \) вершинами называется \( \small n- \)угольником.

На рисунке 1 представлены различные виды многоугольников.

Обозначение многоугольника

Обозначают многоугольник буквами, стоящих при его вершинах. Называют многоугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, многоугольник на рисунке 2 называют \( \small A_1A_2A_3A_4A_5A_6 \) или \( \small A_6A_5A_4A_3A_2A_1 \).

Соседние вершины многоугольника

Вершины многоугольника называются соседними, если они являются концами одной из его сторон.

На рисунке 2 вершины \( \small A_2 \) и \( \small A_3 \) являются соседними, так как они являются концами стороны \( \small A_2A_3. \)

Смежные стороны многоугольника

Стороны многоугольника называются смежными, если они имеют общую вершину.

На рисунке 2 стороны \( \small A_4A_5 \) и \( \small A_5A_6 \) являются смежными, так как они имеют общую вершину \( \small A_5. \)

Простой многоугольник. Самопересекающийся многоугольник

Многоугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).

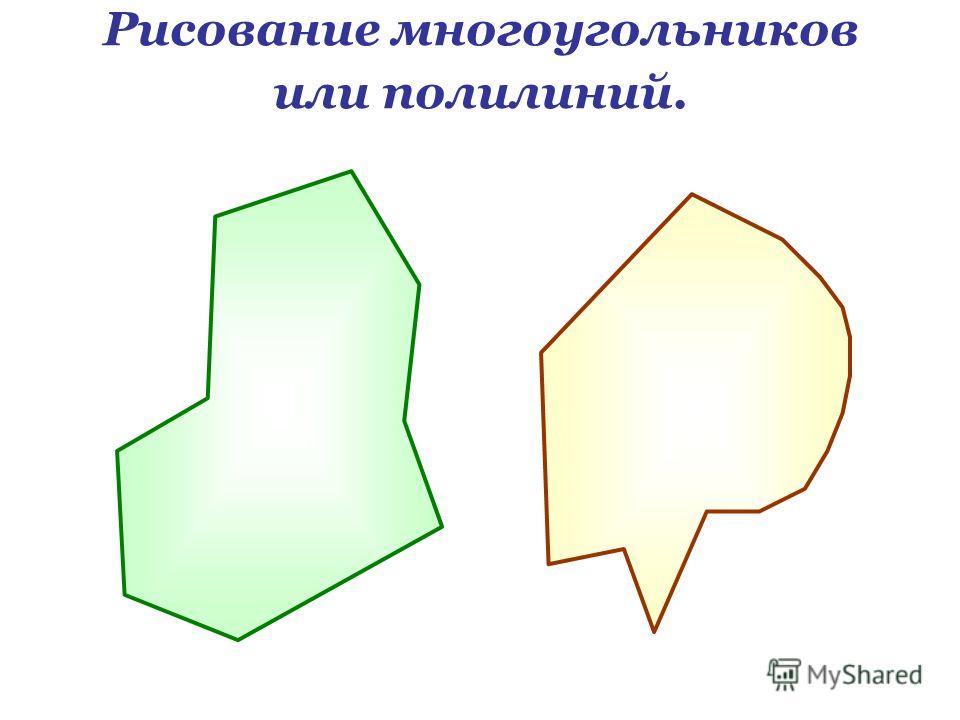
На рисунке 3 изображен простой многоугольник так как стороны многоугольника не имеют самопересечений. А на рисунке 4 многоугольник не является простым, так как стороны \( \small A_1A_4 \) и \( \small A_2A_3 \) пересекаются. Такой многоугольник называется самопересекающийся многоугольник.

Выпуклый многоугольник

Многоугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.

На рисунке 5 многоугольник лежит по одну сторону от прямых \( \small m, \ n, \ l, \ p, \ q, \ r\) проходящих через стороны многоугольника.

На рисунке 6 прямая \( \small m\) делит многоугольник на две части, т.е. многоугольник не лежит по одну сторону от прямой \( \small m\). Следовательно многоугольник не является выпуклым.

Правильный многоугольник

Простой многоугольник называется правильным, если все его стороны равны и все углы равны. Например равносторонний треугольник является правильным многоугольником, поскольку все его стороны равны, и все его углы равны 60°. Квадрат является правильным многоугольником, так как все его стороны равны и все его углы равны 90°.

На рисунке 7 изображен правильный многоугольник (пятиугольник), так как у данного многоугольника все стороны равны и все углы равны. Многоугольник (ромб) на на рисунке 8 не является правильным, так как все стороны многоугольника равны, но все углы многоугольника не равны друг другу. Прямоугольник также не является правильным многоугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.

Звездчатый многоугольник

Самопересекающийся многоугольник, все стороны которого равны и все углы равны, называется звездчатым или звездчато-правильным.

На рисунке 9 представлен звездчатый пятиугольник поскольку все углы \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5 \) равны и равны все стороны: \( \small A_1A_2=A_2A_3=A_3A_4=A_4A_5=A_5A_1. \)

Периметр многоугольника

Сумма всех сторон многоугольника называется периметром многоугольника.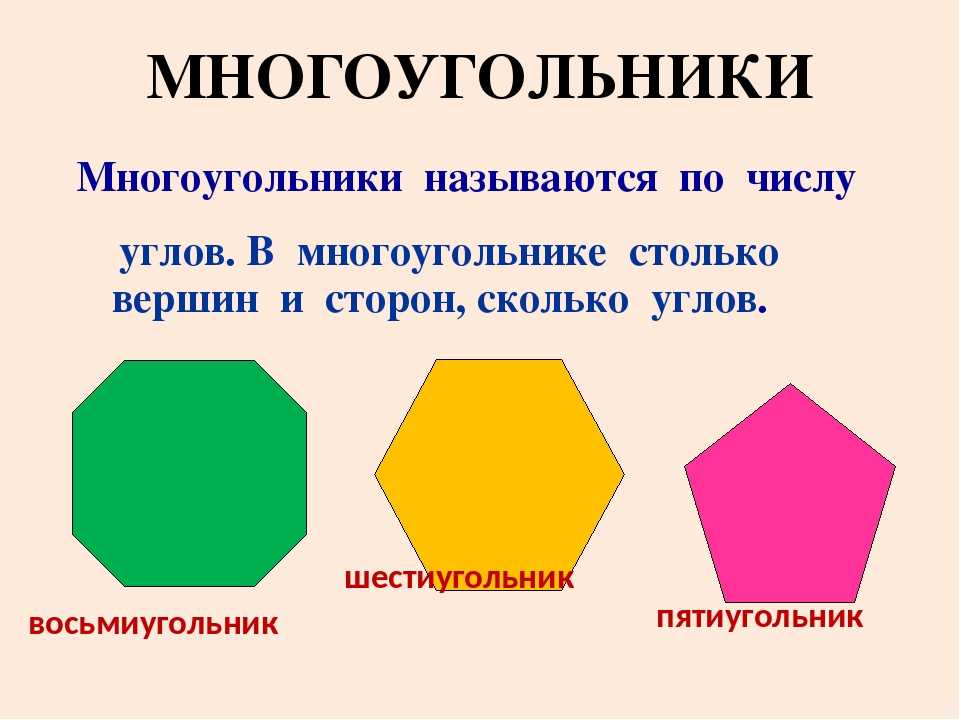 Для многоугольника \( \small A_1A_2…A_{n-1}A_n \) периметр вычисляется из формулы:

\( \small P=A_1A_2+A_2A_3+…+A_{n-1}A_n+A_nA_1 \)

Угол многоугольника

Углом (внутренним углом) многоугольника при данной вершине называется угол между двумя сторонами многоугольника, сходящимися к этой вершине. Если многоугольник выпуклый, то все углы многоугольника меньше 180°. Если же многоугольник невыпуклый, то он имеет внутренний угол больше 180° (угол \( \small A_3 \) на рисунке 2).

Внешний угол многоугольника

Внешним углом многоугольника при данной вершине называется угол смежный внутреннему углу многоугольника при данной вершине.

На рисунке 10 угол 1 является внешним углом данного многоугольника при вершине \( \small E. \)

Диагональ многоугольника. Количество диагоналей

Диагоналями называют отрезки, соединяющие две несоседние вершины многоугольника.

Выведем форулу вычисления количества диагоналей многоугольника. Пусть задан \( \small n \)-угольник. Выберем одну вершину многоугольника и проведем мысленно все отрезки, соединяющие эту вершину с остальными вершинами. Получим \( \small n-1 \) отрезков. Но поскольку две вершины для выбранной вершины являются соседними, а по определнию диагональ − это отрезок соединяющий несоседние вершины, то из \( \small n-1 \) вычтем 2. Получим \( \small n-3 \). Всего \( \small n \) вершин. Следовательно количество вычисленных диагоналей будет \( \small n(n-3). \) Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей \( \small n- \)мерного многоугольника:

Сумма углов выпуклого многоугольника

Выведем формулу вычисления суммы углов выпуклого многоугольника. Для этого проведем из вершины \( \small A_1 \) все диагноали многоугольника \( \small A_1A_2. ..A_{n-1}A_n \) (Рис.11):

Количество диагоналей, проведенной из одной вершиы, как выяснили из предыдующего параграфа равно \( \small n-3 \). Следовательно, эти диагонали разделяют многоугольник на \( \small n-3+1=n-2 \) треугольников. Поскольку сумма углов треугольника равна 180°, то получим, что сумма углов выпуклого многоугольника равна: \( \small 180°(n-2). \)

\( \small 180°(n-2), \)

(1)

где \( \small n \) −количество сторон (вершин) выпуклого многоугольника.

Угол правильного многоугольника

Поскольку у правильного многоугольника все углы равны, то используя формулу (1) получим угол правильного многоугольника:

\( \small \alpha_i=\frac{\large n-2}{\large n} \cdot 180°, \)

где \( \small n \) −количество сторон (вершин) правильного многоугольника.

Многоугольники. Выпуклый многоугольник. Четырехугольник 8 класс онлайн-подготовка на Ростелеком Лицей

Многоугольники.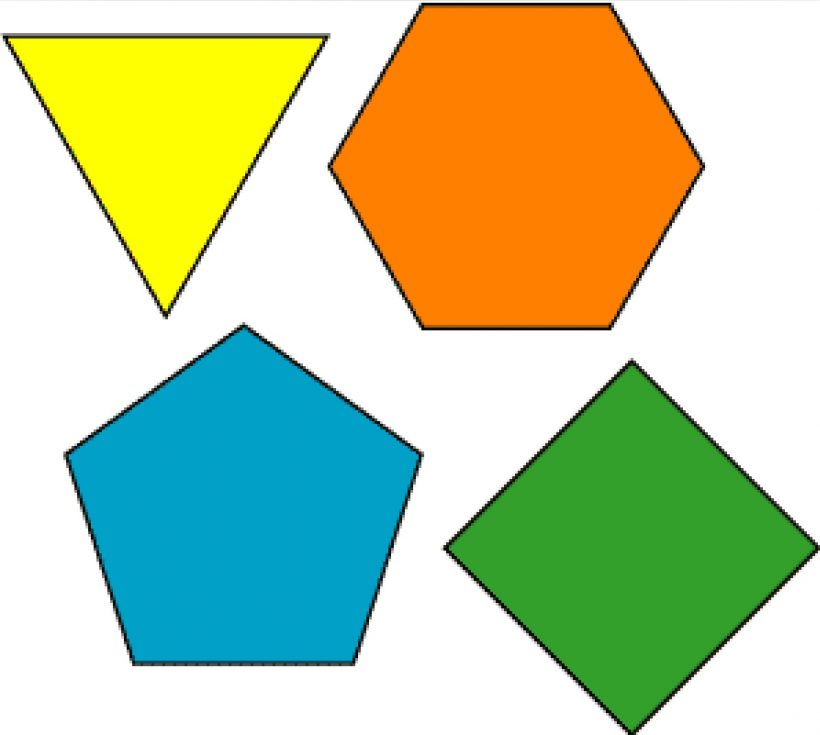 Выпуклый многоугольник. Четырехугольник.

Треугольник – это частный случай многоугольника.

 

 

В самом названии уже подчеркивается, что это фигура, у которой три угла. Следовательно, в многоугольнике их может быть много, т.е. больше, чем три. Например, изобразим пятиугольник – фигуру с пятью углами.

Многоугольник – фигура, состоящая из нескольких точек (больше двух) и соответствующего количества отрезков, которые их последовательно соединяют. Эти точки называются вершинами многоугольника, а отрезки – сторонами. При этом никакие две смежные стороны не лежат на одной прямой и никакие две несмежные стороны не пересекаются.

Любой многоугольник разделяет плоскость на две области: внутреннюю и внешнюю. Внутреннюю область также относят к многоугольнику.

Иными словами, например, когда говорят о пятиугольнике А₁А₂А₃А₄А₅, имеют в виду и всю его внутреннюю область, и границу. А ко внутренней области относятся и все точки, которые лежат внутри многоугольника.

 

 

Многоугольники еще иногда называют n-угольниками, чтобы подчеркнуть, что рассматривается общий случай наличия какого-то неизвестного количества углов (n штук).

Периметр многоугольника – сумма длин сторон многоугольника.

Отрезок, соединяющий любые две противоположные вершины, называется диагональю многоугольника.

 

 

Многоугольники делятся на выпуклые и невыпуклые. Например, многоугольник, изображенный на рисунке выше, является выпуклым, а на рисунке ниже – невыпуклым.

 

 

Многоугольник называется выпуклым, если при проведении прямой через любую из его сторон весь многоугольник лежит только по одну сторону от этой прямой. Невыпуклыми являются все остальные многоугольники.

Правильный многоугольник – это выпуклый многоугольник, у которого все стороны и углы равны.

Существенное отличие четырехугольника от треугольника в том, что он может быть выпуклым или невыпуклым.

 

 

 

Очень важное различие, о котором знает каждый плотник, состоит в том, что треугольник – «жесткая» фигура, а четырехугольник (как и все остальные многоугольники) – «нежесткая».

У треугольника невозможно изменить его форму, не изменив длин сторон. При этом у любого четырехугольника можно изменить его форму, не меняя длины сторон. На практике это будет означать, что треугольник, сколоченный из трех дощечек, будет жестким, не будет сминаться даже при сильных воздействиях, а четырехугольник при достаточной нагрузке со стороны изменит свою форму.

Для описания свойств многоугольников существуют две важнейшие теоремы об их углах: теорема о сумме внутренних углов выпуклого многоугольникаитеорема о сумме внешних углов выпуклого многоугольника.

Теорема. О сумме внутренних углов выпуклого многоугольника (n-угольника).

Сумма углов n-угольника равна 180°·(n-2).

Математическая запись: ∠A1+∠A2+…+∠An=180°(n-2), где n – количество его углов (сторон).

Вспомним, что любой четырехугольник состоит из двух треугольников (достаточно провести диагональ). Но сумма углов каждого из них одинакова и равна 180⁰, значит, сумма углов четырехугольника 360⁰.

Теорема. О сумме внешних углов выпуклого многоугольника (n-угольника).

∠1’+∠2’+…+∠n’=360°, где n – количество его углов (сторон), а ∠1′,…,∠n’ – внешние углы, по одному от каждой вершины.

ИНЖЕНЕРНЫЙ ЧЕРТЕЖ- Многоугольник — УЧЕБНЫЕ МАТЕРИАЛЫ

Многоугольник – плоская фигура, ограниченная множеством (обычно пятью и более) прямых линий.

Когда все стороны и углы между ними равны, он называется ПРАВИЛЬНЫМ МНОГОУГОЛЬНИКОМ.

 

 

Когда все стороны и углы между ними не равны, он называется НЕПРАВИЛЬНЫМ МНОГОУГОЛЬНИКОМ.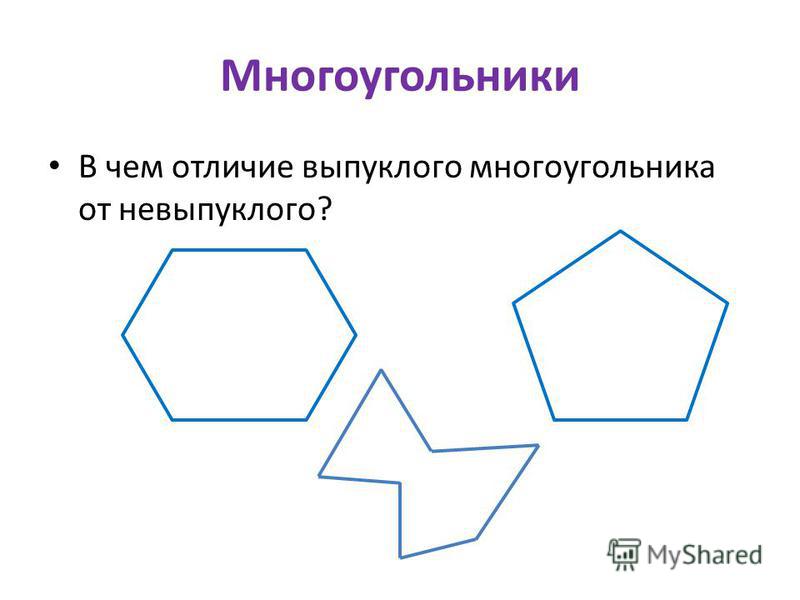

Многоугольники именуются по количеству сторон, как указано ниже:

С. №	ИМЯ	КОЛИЧЕСТВО СТОРОН
и	ПЕНТАГОН	5
б	ШЕСТИГРАННИК	6
с	СЕМЯУГОЛЬНИК	7
д	ВОСЬМИУГОЛЬНИК	8
и	НОНАГОН	9
ф	ДЕКАГОН	10
г	ДЕСЯТИУГОЛЬНИК	11
ч	ДВУДЕКАГОННЫЙ	12

 

СВОЙСТВА МНОГОУГОЛЬНИКА:

• Все углы правильного многоугольника лежат на окружности. Стороны правильного многоугольника будут касаться окружности, нарисованной внутри.

 

 

• Сумма внутренних углов многоугольника равна (2 x n – 4) x прямой угол, где n – количество сторон.

• Сумма внешних углов многоугольника равна 360°.

 

 

• Сумма внутреннего угла и соответствующего внешнего угла составляет 180°.

 

Нарисуйте правильный семиугольник со стороной 25 мм.

 

Метод полукругов

• Проведите линию АВ длиной 25 мм.

• Удлините BA на удобную длину.

• `A’ как центр и радиус AB описывают полукруг.

• Разделите полукруг на семь равных частей (количество сторон) с помощью делителя.

• Пронумеруйте точки 1,2,3,4,5,6, начиная с «P».

• Присоединение A2

• Проведите серединные перпендикуляры из точек 2А и АВ, пересекающиеся в точке 0,9.0114

• `0′ в качестве центра и OA или OB в качестве радиуса описывают окружность.

• Отметьте на окружности точки C,D,E,F и 2 так, чтобы BC = CD = DE = EF = F2 = AB.

• Соедините линии BC, CD, DE, EF и F2.

• ABCDEF2 требуется семиугольник.

 

Метод полукруга

 

Выполните процедуру до разделения полукруга на количество равных частей.

• Присоединиться к A2.

• Соедините листы A3, A4, A5 и A6 и удлините до нужной длины.

• С центром «B» и радиусом AB нарисуйте дугу, пересекающую удлиненную линию A6 в точке «C».

• «C» в качестве центра и того же радиуса, нарисуйте дугу, пересекающую линию A5 в точке «D».

• Таким же образом найдите точки E и F.

• Присоединяйтесь к BC, CD, DE, EF и F2.

• ABCDEF2 — искомый семиугольник.

 

Нарисуйте пятиугольник внутри круга диаметром 60 мм.

 

• Проведите линию AH, равную 60 мм. (Диаметр круга).

• «O» как центр OA как радиус описывает окружность.

• Разделите AH на 5 равных частей (столько равных частей, сколько сторон).

• A и H как центры, AH как радиус описывают дуги, пересекающиеся в точке «P».

• Присоединитесь к P2 и удлините его, чтобы встретить круг в точке «B».

• Зачет BC, CD, DE, EF равен AB на окружности.

• Соедините точки.

• ABCDEF — искомый пятиугольник.

 

Начертите шестиугольник (описанный описанием) со стороной 32 мм дуговым методом.

 

• Нарисуйте окружность радиусом 32 мм.

• Отметьте диаметр AD.

• С одинаковым радиусом, A и D как центры. Нарисуйте две дуги, пересекающие окружность в точках B, F, E и C соответственно.

• Присоединяйтесь к AB, BC, CD, DE, EF и FA.

• ABCDE — требуемый шестиугольник.

 

Нарисуйте шестиугольник внутри круга диаметром 60 мм (вписав).

 

• Проведите линию FC, равную 60 мм (диаметр круга).

• «О» как центр описывает окружность на диаметре FC.

• F как центр FO как радиус, нарисуйте дугу в точке A.

• «А» в центре, того же радиуса, нарисуйте дугу в точке В.

• Таким же образом установите точки C, D и E.

• Присоединяйтесь к AB, BC, CD, DE, EF и FA.

• ABCDEF — требуемый шестиугольник.

 

Начертите шестиугольник методом поперек плоскости.

 

Шестигранник, расстояние по плоскости 45 мм

• Начертите окружность Φ 45. (45 мм — размер по плоскости).

• Проведите две горизонтальные касательные BC и FE.

• С квадратом 60° проведите четыре касательные, касающиеся горизонтальных касательных.

• Отметьте углы A, B, C, D, E и F.

• ABCDEF — требуемый шестиугольник.

 

 

редактирование — Как исправить ошибки при рисовании полигона или линии в QGIS?

спросил 8 лет, 6 месяцев назад

Изменено 1 месяц назад

Просмотрено 11 тысяч раз

При рисовании больших многоугольников или длинных непрерывных линий в QGIS я склонен ошибаться.

Затем каждый раз, когда я ошибаюсь, я не нахожу способа отменить эту последнюю точку (или несколько последних точек) и начать заново рисовать многоугольник или линию.

• qgis
• редактирование
• создание полигонов
• создание полилиний

0

Последние вставленные вершины можно удалить одну за другой, нажав клавиши Del или BackSpace.

Кажется, что это действительно недокументировано в текущем руководстве QGIS 2.2 по адресу http://docs.qgis.org/2.0/en/docs/user_manual/working_with_vector/editing_geometry_attributes.html. Он будет относиться к разделу «Добавление объектов», в котором на данный момент рассказывается только о том, как добавить вершины и закончить оцифровку.

Для линий и многоугольников продолжайте щелкать левой кнопкой мыши для каждого дополнительного точка, которую вы хотите зафиксировать. Когда вы закончите добавлять точки, щелкните правой кнопкой мыши в любом месте области карты, чтобы подтвердить, что вы закончили ввод геометрии этого объекта.

Delete/Backspace у меня не сработало, но Control+Z сработало.

Чтобы отменить последний шаг при рисовании многоугольника в QGIS, используйте DELETE или BACKSPACE один раз.

если необходимо вернуться на несколько шагов назад, нажмите DELETE или BACKSPACE необходимое количество раз, пока не отмените необходимое количество шагов.