Теорема пчелиных сот: МАТЕМАТИЧЕСКИЕ ТАЙНЫ ПЧЕЛИНОЙ ЯЧЕЙКИ

Содержание

Проект по геометрии «Геометрия пчелиных сот» – Документ 1 – УчМет

— 4 —

МОУСОШ№2 имени Героя Советского Союза А.В.Ляпидевского гЕйска МО Ейский район.

«Геометрия пчелиных сот»

Выполнила:

Дроздова Яна , ученица 8Б класса

Руководитель:

Бобровникова Т.В.

учитель математики

гЕйск 2012г

Актуальность работы. Умение применять знания школьного курса геометрии в жизни, что способствует расширению кругозора и уделение более пристального внимания школьному материалу.

Цель работы. Для полного раскрытия темы ставится следующая цель: умение решать задачи практического характера, с применением приобретенных знаний в школе; расширение кругозора в ходе исследования, а так же показать связь математики с жизнью и эффективность математики.

Постановка задач. Достижение поставленной цели возможно путем рассмотрения следующих задач: 1) доказательство составления паркета из правильных многоугольников: 2) выявления правильного многоугольника с наименьшим периметром; 3) применение геометрических построений при рассмотрении пчелиных ячеек сот;

4) выявление наименьшей площади поверхности многогранника.

Объект исследования. Объектом изучения работы является пчела, ее соты.

Содержание работы.

— начало исследования – знакомство с интересной задачей про пчел, а так же наблюдение

за строительством пчелиных сот;

— причины, по которым строительство ячеек сот соответствует правильному

шестиугольнику;

— принцип построения паркетов из правильных многоугольников;

— выявление наименьшего периметра правильного многоугольника с применением формул

нахождения площадей, сторон и периметров этих многоугольников;

— построение одной ячейки с применением геометрических построений и знанием

пространственных тел- многогранников.

— сравнение площадей поверхности многогранников и пчелиной ячейки;

— геометрические способности пчел помогают им экономить время, воск и силы.

Выводы по работе.

В заключении мне бы хотелось сказать, что геометрический подход к природным явлениям позволяет увидеть внутренний мир, гармонию, структуру этого явления.

А исследования, проведенные в ходе работы, знакомят и сближают нас с гармонией

и целесообразностью природы.

Оглавление.

1. Вступление.

Связывая природу, математику, и искусство, можно убедиться

в том, что для тех, кто стоял у истоков искусства, природа и

человек были образцами для подражания. Есть такие творения

природы, которых человек порой не замечает___________________стр2.

2. Основная часть.

1) Сеть правильных шестиугольников_______________________стр3.

2) Паркет:

а) формулировка задачи о составлении паркета____________стр3.

б) доказательство задачи_______________________________стр4.

в) составление паркета из правильного треугольника,

квадрата и правильного шестиугольника_______________стр5.

3) Расчетливая геометрия:

а) доказательство того, что периметр правильного

шестиугольника наименьший из периметров

остальных правильных многоугольников ______________стр6.

б) построение ячейки пчелиных сот, и их проекции_________стр8.

в) доказательство того, что площадь поверхности

пчелиной ячейки наименьшая из поверхностей

других многогранников, имеющих одинаковый

объем____________________________________________стр10.

3. Заключение.

Всесторонняя эффективность математики___________________стр11.

4. Список литературы ____________________________________стр12

Введение

Пчёлы – удивительные творения природы. Геометрические способности пчёл проявляются при построении сот. Если разрезать пчелиные соты плоскостью, перпендикулярной их рёбрам, то будет видна сеть правильных шестиугольников, уложенных в виде паркета.

Возникает вопрос: «Почему пчёлы строят соты именно так, почему они предпочли сеть правильных шестиугольников, а не правильных треугольников или квадратов, ведь их, казалось бы, гораздо проще сконструировать?»

В учебнике за пятый класс есть очень интересная задача о пчёлах. А так как мы сами разводим пчёл, то я решила обратить на неё наиболее пристальное внимание.

Задача №1:

Чтобы собрать 100 грамм мёда, пчела доставляет в улей 16 тысяч нош нектара. Вопрос задачи: какова масса одной ноши?

Решение:

100 : 16000=0,00625 (г) -масса одной ноши.

Ответ: 0,00625 грамм.

А умещает пчела свою ношу на своей ножке в мешочке.

Решив эту задачу, можно сделать следующий вывод: пчела очень трудолюбива, прикладывает огромные усилия для того чтобы, собрать мёд.

Собирая нектар с цветков, пчела «налетает» около трёхсот километров, посетив при этом девятнадцать миллионов цветков. А несколько килограммов мёда – это уже несколько километров. Скорость полёта пчелы – 6,5 километров в час. Продолжительность жизни пчелы 30-35 дней.

2.Основная часть.

Теперь попытаемся ответить на вопрос: «Почему пчелы строят соты именно так, почему они предпочли сеть правильных шестиугольников, а не правильных треугольников или квадратов?

Чтобы ответить на этот вопрос, необходимо предварительно выяснить, какими правильными многоугольниками можно заполнить плоскость так, чтобы не было пропусков, то есть уложить их в виде паркета.

Выполняя несложные расчёты, убеждаемся, что такими многоугольниками могут быть только квадраты, правильные треугольники и правильные шестиугольники.

Квадрат правильный треугольник правильный шестиугольник.

Задача №2:

Действительно, сумма внутренних углов выпуклого n-угольника равна

(n-2)·180º, где n-число сторон многоугольника. Сумма углов правильных n-угольников, сходящихся в одной вершине паркета, равна 360º. Тогда приравняв сумму внутренних углов к числу 360, мы получим следующее равенство: .

Решаем это уравнение относительно числа к, тогда получим:

или ,

где k — число углов, сходящихся в одной вершине паркета.

Отсюда .

Рассмотрим некоторые правильные многоугольники.

1). Возьмём треугольник с количеством сторон равным трём.

Тогда, если n=3, то k=6. А это значит, что в одной вершине паркета могут сходиться шесть правильных шестиугольников;

2). Возьмём квадрат с количеством сторон равным четырём.

Тогда, если n=4, то k=4, то есть в одной вершине паркета могут сходиться четыре квадрата.

3). Возьмём пятиугольник с количеством сторон равным пяти.

Если n=5, то k=3,3. А так как k получили не целое число, то не существует паркета из правильных пятиугольников.

4). Возьмём шестиугольник с количеством сторон равным шести.

Тогда, если n=6, то k=3, то есть в одной вершине паркета могут сходиться три правильных шестиугольника;

5). Возьмём семиугольник с количеством сторон равным семи.

Если n=7, то k=2,8. А так как k получили не целое число, то не существует паркета из правильных семиугольников. И так можно продолжать дальше.

Теперь рассуждаем следующим образом: ,так как внутренний угол правильного многоугольника меньше 180º;

значит,

или

По смыслу задачи значения n, k и могут быть только целыми , поэтому 4 делится нацело на (n-2). Отсюда n = 3,4,6.

Итак, мы выяснили, что заполнить плоскость без пропусков можно, используя или правильные треугольники, или квадраты, или правильные шестиугольники. Только ими можно уложить паркет без пропусков.

Паркеты:

1) из правильных треугольников

2) из правильных четырехугольников

3) из правильных шестиугольников

Попробуем дальше развить «пчелиную» тему.

Для того чтобы выяснить, почему пчела строит соты, перпендикулярное сечение которых есть правильный шестиугольник, а не правильный треугольник или квадрат, рассмотрим вспомогательную задачу.

Задача №3: Даны три равновеликие друг другу фигуры – правильный треугольник, квадрат, правильный шестиугольник. Какая из данных фигур имеет наименьший периметр?

Дано: правильный треугольник, квадрат, правильный треугольник. S – из правильных многоугольников. . S=4 см²

Найти: периметр каждого правильного многоугольника.

Решение:

Пусть S – площадь каждой из данных фигур.

а₃, а₄, а₆ — стороны соответствующих многоугольников.

S=4 см².

1). Тогда вычислим площадь треугольника по формуле:

Подставив данные правильного треугольника в эту формулу, получим:

2). Площадь квадрата вычислим по формуле:

3). Площадь правильного шестиугольника состоит из шести площадей правильного треугольника. Тогда получим:

Теперь нетрудно вычислить периметр каждой фигуры, зная её площадь.

Сначала выразим сторону каждого многоугольника через его площадь, затем найдем периметр этого многоугольника:

, тогда .

Подставив в формулу значение площади, равное 4 см², получим, что

Р ≈ 9,1 см.

Аналогично выразим сторону квадрата через его площадь и найдем периметр квадрата при заданном значении его площади:

, тогда , значит

Р = 8 см.

Осталось выразить сторону правильного шестиугольника через его площадь и найти периметр:

, тогда , получим:

Р ≈ 4,6 см.

Для сравнения периметров фигур найдём их отношение:

Мы видим, что из трёх правильных многоугольников с одинаковой площадью наименьший периметр имеет правильный шестиугольник. Стало быть, выбрав правильный шестиугольник, мудрые пчёлы экономят воск и время для построения сот.

Надо сказать, что на этом математические секреты пчёл не заканчиваются. Интересно и дальше исследовать строение пчелиных сот.

Соты в улье свешиваются сверху вниз наподобие занавесок:

пчёлы прикрепляют их к потолку смесью воска или пчелиного клея (прополиса). Ячейки уложены в пласты и соприкасаются общими донышками.

Но донышки ячеек не плоские, а представляют собой части трёхгранных углов, гранями которых являются равные ромбы.

Рис.2.

Рис. 1.

На рисунке 1 изображена пчелиная ячейка в общем виде, а на рисунке 2 – её проекции: вид сверху, вид спереди и вид сбоку.

Попробуем построить развёртку многогранника (одна ячейка сот). Но прежде чем начать построение сот развёрстки, необходимо рассмотреть чисто геометрически, как получается ячейка.

Сначала построим изображение правильной шестиугольной призмы. Проведём диагонали верхнего основания призмы и на оси призмы возьмём некоторую точку S. Через прямые и точку S проводим три плоскости, которые отсекают от призмы три равные треугольные пирамиды . Получившийся многогранник и является пчелиной ячейкой.

Поскольку боковая поверхность многогранника представляет собой шесть равных между собой трапеций, то для получения развёртки построим эти трапеции. Их размеры возьмём такими же, как на рисунке 2 , причём отрезок MS на рисунке 2, a-это диагональ ромба в верхней части ячейки.

Построим отрезок AA´=AB+BC+CD+DE+EF+FA (рисунок 4). На продолжении ребра CL от точки L отложим отрезок LS и из точки L проведём окружность радиусом, равным, например, отрезку. После этого построим середину отрезка LS, проведём через неё перпендикулярную к нему

Рис. 4.

прямую, которая пересекает дугу окружности в двух вершинах ромба. Два других ромба строим следующим образом: из вершины ромба проводим окружность радиусом, равным стороне построенного ромба, а из вершины S – окружность, радиус которой равен диагонали ромба. Эти окружности в пересечении дают ещё одну вершину ромба. Остальные построения очень просты. Развёртка пчелиной ячейки показана на рисунке 4.

. А на рисунке 5 можно увидеть, как соприкасаются ячейки в улье; их общая часть является ромбом.

Когда говорят о пчёлах, то чаще всего демонстрируют рисунок 6 , показывающий соты в разрезе плоскостью, перпендикулярной боковому ребру и пересекающей все соты по правильным шестиугольникам.

Рис.6.

Если продолжить одну из боковых граней ячейки так, чтобы она пересекала остальные соты, то сечение будет таким, как показано на рисунке 7.

Рис. 7.

Небезынтересен вопрос, почему пчёлы строят донышки своих ячеек в форме части трёхгранного угла, в качестве граней которого служат ромбы. Нельзя ли было поступить проще, сделать дно сот плоским, то есть обычным правильным шестиугольником? Какая же здесь выгода для пчёл?

Вернёмся к ячейке-многограннику на рисунке 3. Объём многогранника

равен объёму правильной шестиугольной призмы. Как нетрудно заметить, объём пирамиды равен утроенному объёму одной из равных пирамид.

Пирамиды и равны (они симметричны относительно точки Т). Мы можем самостоятельно провести доказательство равенства названных пирамид, оно несложно. Итак, объёмы пчелиной ячейки и правильной шестиугольной призмы равны.

Зато площадь ее поверхности меньше площади поверхности шестиугольной призмы.

3. Заключение.

В имеющейся литературе приводятся сведения о том, что благодаря такой «математической» работе расчётливые «геометры» экономят около 2 % воска. Количество воска, сэкономленного при постройке 54 ячеек, может быть использовано для одной такой же ячейки.

В итоге необходимо сказать, что пчелиные соты представляют собой пространственный паркет, поскольку заполняют пространство так, что не остаётся просветов.

Как в заключение не согласиться с мнением Пчелы из сказки «Тысяча и одна ночь»:

«Мой дом построен по законам самой строгой архитектуры. Сам Евклид мог бы поучиться, познавая геометрию моих сот».

Так с помощью геометрии и математического анализа мы прикоснулись к тайне математических шедевров из воска, ещё раз убедившись во всесторонней эффективности математики.

4. Список литературы:

1) А.И.Азевич «Двадцать уроков гармонии» — гуманитарно – математический

цикл;

2)Журнал: «Математика в школе» №1 1995 г.

3) Журнал: «Пчеловод», подшивка за 2001 год.;

4) Детская энциклопедия: «Что? Где? Почему?»

5) Учебник: «Геометрия 7-11 класс» Погорелов;

6) Учебник: « Математика 5 класс» Виленкин.

Открытый урок «Правильные многоугольники в природе(геометрия пчелиных сот)» | План-конспект урока по геометрии (9 класс) на тему:

Муниципальное бюджетное общеобразовательное учреждение

«Средняя общеобразовательная школа № 5»

Тема :«Правильные многоугольники в природе

(геометрия пчелинных сот)»

9 класс

учителя математики

МБОУ «Средняя

школа № 5» г. Курска

ТЕВЯШЕВОЙ О.М.

Курск — 2013

Цели урока:

Повторить формулы зависимости между стороной правильного многоугольника и его площадью и периметром; использовать их для решения задач.
Развивать познавательный интерес учащихся, учить видеть связь между математикой и окружающей жизнью.
Воспитывать любовь и интерес к живой природе, учить трудолюбию, аккуратности, внимательности ко всему окружающему.

Тип урока:обобщающий урок по теме «Правильные многоугольники».

Оборудование: шаблоны правильных многоугольников: треугольников, квадратов, шестиугольников, пятиугольников, восьмиугольников, двенадцатиугольников – каждого типа по 6 штук ( все многоугольники с одинаковой длиной стороны).

Ход урока.

Сообщение учителя.

Правильные многоугольники встречаются в природе. Один из примеров – пчелинные соты, которые представляют собой прямоугольник, покрытый ( т. е. составленный без просветов и перекрытий) правильными шестиугольниками (рис. 1). На этих шестиугольниках пчёлы наращивают их воска ячейки, представляющие собой прямые шестиугольные призмы. В них пчёлы и откладывают мёд, а затем снова покрывают сплошным прямоугольником из воска.

Чарльз Дарвин отмечает: «Далее этой ступени совершенства в архитектуре естественный отбор не мог вести, потому что соты пчёл абсолютно совершенны с точки зрения экономии труда и воска».

Геометрия пчелинных сот, жизнь и деятельность пчёл всегда привлекала внимание человека. «Странные общественные привычки и геометрические дарования пчёл, -пишет известный математик Герман Вейль, — не могли не привлечь внимания и не вызвать восхищения людей, наблюдавших их жизнь и использовавших плоды их деятельности».

Решение задач.

Задача1.

Пчелинные соты представляют собой прямоугольник, покрытый правильными шестиугольниками ( рис. 1). Найти, какими ещё правильными многоугольниками можно покрыть плоскость.

Решение.

Способ I (метод уравнений ).

Предположим, что плоскость покрыта правильными п-угольниками, причём каждая вершина является общей для х таких многоугольников, - внутренний угол правильного многоугольника, равный  = 1800 (n — 2)

(рис. 2,а) n

а) б)

рис.2

Тогда 1800 (n — 2)x = 3600

Из этого равенства находим х = 2n = 2 + 4

n-2 n-2

Учитывая, что х – целое, получаем п = 3, 4, 6.

Итак, плоскость можно покрыть рпавильными ттреугольниками, квадратами и правильными шестиугольниками.

Способ II ( метод перебора).

п = 3 Три угла, плотно составленные, составляют 1800, шесть углов – 3600.

Плоскость покрыта без просветов (рис. 3,а).

п = 4 Четыре угла вместе дают 3600, т. е. 900  4 = 3600, плоскость покрыта без

просветов ( рис. 3,б).

п = 5 Внутренний угол правильного пятиугольника равен 1080,

1080  3 = 3240. остаётся просвет в 360 (рис. 3,в). плоскость без просветов не

покрывается.

п = 6 внутренний угол правильного шестиугольника равен 1200, три шестиугольника, составленные вместе, образуют 1200 3 = 3600. плоскость покрывается без просветов

(рис. 3, г).

а) б)

в) г)

рис. 3

Метод перебора можно продолжать и дальше; итогом решения будет вывод, что плоскость без просветов можно покрыть лишь правильными треугольниками, квадратами и правильными шестиугольниками (если многоугольники одного вида).

Задача 2.

Почему пчёлы выбрали именно шестиугольник? Для ответа на этот вопрос нужно сравнить периметры разных многоугольников, имеющих одинаковую площадь. Пусть даны правильный треугольник, квадрат и правильный шестиугольник. У какого из этих многоугольников наименьший периметр?

Решение.

Способ I. Пусть площадь правильного п-угольника равна Sп, А1А2 = ап (рис. 2, б):

Sп = пап2__ ; Итак, Sп = пап2 ctg(1800), А1ОН = 1800, ап- сторона п- угольника,

4tg (1800/п). 4 n n А1ОА2 = 3600.

Отсюда S3 = 3  а32, S4 = а42, S6 = 33 а62. n

4 2

Так как все площади равны, обозначим их S. Тогда:

а32= 4S, а42= S , а62 = 2S.

3 33

Для удобства сравнения возведём Рп в степень. Имеем Рп = пап, где Рп – периметр п-угольника, т. е. Р3 = 3 а3, Р32 = 9 а32 , Р34 = 81 а34 = 432 S2.

Аналогично получим Р44 = 256 S2, Р64 = 192 S2.

Например, S = 16см2, при а3 = 6 см, а4= 4 см , а6 = 2, 5 см.

Сравнив степени периметров, приходим к выводу, что наименьший периметр при одинаковой площади у шестиугольника!

Способ II.

Пусть имеем АВСDEF – правильный шестиугольник, А/ В/С/D/– квадрат,

А/В/С/ – правильный треугольник (рис. 4).

Обозначим Sп – площадь, Рп пермметр п- угольника, АВ = а.

Тогда S6 = 33а2 ≈2,55а2 , Р6 = 6а

рис.4

Все площади равны, а значит, имеем:

S4 = 2,44а2, А1В1 ≈1,6а. Отсюда Р4 ≈ 6,4а .

Пусть А2В2 = b. Выразим b через а , тогда S3 = b2∙sin600 = b2√3.

2 4

Но b2√3 = 33а2 , b2 = 6а2 , b = а√6 ≈2,4а , Р3 ≈ 7,2а.

4 2

Итак, периметры многоугольников, имеющих одну и ту же площадь, относятся как

Р6 : Р4 : Р3 = 6 : 6,4 : 7,2 или 3 : 3,2 : 3,6.

Вывод: приусловии одинаковой площади многоугольников наименьший периметр имееет правильный шестиугольник.

Практическая работа

Можно ли без просветов покрыть плоскость многоугольниками, если этими многоуголь-никами являются правильный шестиугольник и квадрат, имеющие одинаковые стороны?

Учащиеся выполняют работу, используя готовые шаблоны: покрывают плоскость многоугольниками, получают при этом просвет в 600.

Вопрос. Где человек может использовать умение покрывать плоскость правильными многоугольниками?

Ответ. При составлении различных орнаментов, паркета и т. д. можно использовать покрытие плоскости правильными многоугольниками.

Сообщение учителя

На примере пчёл мы убеждаемся, насколько гармонично устроен наш мир, как умна природа. Задача человека — беречь этот мир и разумно пользоваться его дарами. Жизнь и деятельность пчёл вызывает восхищение людей, пчёлами интересуются не только естествоиспытатели. Выдающийся мыслитель и критик XIX века Д. И. Писарев написал в 1862 году статью «Пчёлы», в которой он сравнивает пчелинный улей с государством, проводит аналогию с человеческим обществом . Итак, по Писареву, в улье есть царица – матка, трутни и рабочие пчёлы. Вот рабочие-то пчёлы и строят соты, носят мёд, заполняют ячейки мёдом и закупоривают их. Они кормят весь улей, да и людей – тоже, если человек умело с ними обращается.

Любопытно, что у пчёл пять глаз, чего лишён человек. Два глаза (больших) расположены по бокам головы и играют роль микроскопов, а другие три крошечных глаза расположены в верхней части головы, ими пчёлы пользуются при полёте. Благодаря этим глазкам пчела видит очень далеко.

Перелетая от цветка к цветку, эти насекомые опыляют растения, одновременно собирая цветочный нектар и перенося его в соты. Масса одной пчелинной ноши нектара около 6 мг. Чтобы накопить в улье 50 г мёда, пчела должна сделать примерно 8333 вылета. А для получения 100 г мёда пчела должна облететь почти миллион цветков, зато при хорошей «лётной» погоде за лето можно получить до 25 кг мёда.

Сообщения учащихся

Учащийся А.

Натуральный пчелинный мёд – ценнейший продукт, он содержит необходимые для жизни человека вещества: сахара, главным образом глюкозу, ферменты, белки, соли кальция, калия, натрия, магния, железа,хлора, фосфора, серы, йода, органическое кислоты (яблочную, лимонную, молочную и др.), эфирное масло, витамины С, В2, В6, Н, К и каротин, пантотеновую и фолиевую кислоты, гормоны, антибиотики – всего более 60 различных веществ, а в некоторых сортах мёда содержится даже радий. Обилие ценных веществ и витаминов делает мёд незаменимым продуктом питания, он широко используется человеком в народной медицине, в косметике. Как лекарственное средство благотворно влияет на желудочную деятельность и сердечную мышцу.

Учащийся Б.

Пчелиное маточное молочко – вещество, которым пчёлы вскармливают личинку будующей матки.

Установлено, что маточное молоко содержит все незаменимые аминокислоты, оказывает на кожу благоприятное действие, востанавливает её эластичность, улучшает обмен веществ, обладает бактерицидным действием. Маточное молочко влияет на кожу как «омолаживающее» средство.

Учащийся В.

Пчёлы строят соты из воска. Воск выделяется особыми железами рабочей пчелы. Воск выделяют только молодые пчёлы от 10-12 дней до 18-20 дней. Чистый воск легче воды, плавится при температуре 60-650. за сезон пчелиная семья может дать 0,8-1,2 кг воска. Из воска готовят свечи, краски. Применяется в косметике.

Учащийся Г.

Кроме мёда, воска, маточного молочка пчёлы дают ещё прополис. Прополис – смолистое вещество, темно-зелёного цвета, горький на вкус, с приятным запахом берёзы. Источником прополиса являются смолистые вещества, собираемые пчёлами с растений. В нём 55% смол, 10% эфирных масел, 30% воска и 5% пыльцы. Хорошо растворяется в спирте и плохо в воде. Температура плавления – 800. Широко используется в медицине.

Итог урока

Учитель.

Итак, не восхищаться пчёлами нельзя. Недарпом у нас развито пчеловодство, в том числе и любительское. Но чтобы управлять этими маленькими тружениками, человек должен любить своё дело, обучаться ему, должен быть аккуратным, терпеливым и трудолюбивым. И тогда природа ответит благодарностью.

Задания для домашней работы

Можно ли без просветов в перекрытий покрыть плоскость правильными многоугольниками, если этими многоугольниками являются:

а) шестиугольник, квадрат и треугольник;

б) восьмиугольник и квадрат;

в) двенадцати угольник и треугольник?

Почему?

2. Соберите рецепты народной медицины. В которых использованы продукты, даваемые пчёлами.

Гипотеза

сот — Wiki | Golden

Гипотеза о сотах утверждает, что при разделении плоскости на области равной площади периметр, по крайней мере, равен периметру правильной шестиугольной мозаики в виде сот. То есть при разделении поверхности на формы равной площади (без промежуточного пространства) шестиугольники располагаются плиткой с наименьшим возможным периметром. Следовательно, шестиугольная структура является наиболее эффективной (использует наименьшее количество материала) для заполнения плоскости ячейками равной площади.

В 1999 году американский математик Томас Хейлз опубликовал доказательство гипотезы о сотах.

История

Около 36 г. до н.э. римский ученый Марк Теренций Варрон писал о шестиугольной структуре пчелиных сот в своей книге по сельскому хозяйству. Варро написал:

Разве камера в гребне не имеет шести углов. . . Геометры доказывают, что этот шестиугольник, вписанный в круглую фигуру, заключает в себе наибольшее пространство.

В 4 веке нашей эры греческий математик Папп Александрийский представил доказательство проблемы в предисловии к своей пятой книге. Однако аргумент Паппа неполный и представляет собой лишь сравнение трех наводящих на размышления случаев (треугольник, квадрат и шестиугольник). Пифагорейцам было известно, что только эти три правильных многоугольника могут замостить плоскость. Папп заявил, что при одинаковом количестве материала для изготовления этих фигур шестиугольник сможет вместить больше всего меда. Его причины ограничиться только этими тремя правильными многоугольниками не были математическими, а основывались на том, что пчелы избегали непохожих фигур. Папп также исключил промежутки между ячейками сот без математических аргументов, заявив:

посторонние предметы могут попасть в промежутки между ними и таким образом осквернить чистоту их продукции.

Изопериметрические свойства сот означают, что на протяжении веков существует огромное количество литературы, в которой пчела упоминается как геометр. Дарвин объяснил сотовую структуру с помощью естественного отбора:

Что движущей силой процесса естественного отбора была экономия воска; тот отдельный рой, который меньше всего тратит меда на выделение воска, преуспевает больше всего.

Гипотеза о сотах была решена при специальных гипотезах, в том числе венгерским математиком Ласло Фейешем Тотом. В 1943 году Тот доказал гипотезу о сотах в рамках гипотезы о выпуклости ячеек. В соответствии с этой гипотезой границы ячеек вынуждены быть многоугольниками, что устраняет потенциальные контрпримеры областей, ограниченных дугами окружности.

В июне 1999 года американский математик Томас Хейлз, работая в Мичиганском университете, доказал гипотезу о шестиугольных сотах без каких-либо специальных гипотез.

Использование изогнутых сторон усложняет проблему, так как стороны могут выпирать, увеличивая площадь. Однако выпячивание одной стороны приводит к тому, что соседняя область выпячивается, уменьшая площадь. Хейлз доказал, что недостатки выпуклости перевешивают преимущества выпуклости, и поэтому многоугольники лучше (и лучше всего правильные шестиугольники), чем ячейки, связанные дугами окружности. Доказательство начинается со сведения к конечным кластерам, что требует предположения о связности областей.

Теорема

Форма теоремы может быть выражена через изопериметрическую константу для правильного N-угольника (многоугольника с N сторонами). есть отношение квадрата длины окружности к площади правильного N-угольника, тогда периметр правильного шестиугольника с единичной площадью равен .

Пусть:

— диск радиуса r в начале координат.

— локально конечный граф, состоящий из гладких кривых и имеющий бесконечно много ограниченных компонент связности, каждая из которых имеет единичную площадь.

— объединение этих ограниченных компонент

Тогда:

Равенство достигается только для правильной шестиугольной плитки.

Шестиугольники в природе

Изопериметрическое свойство шестиугольников, которое позволяет им наиболее эффективно объединять одинаковые клетки в плоской плоскости, означает, что они присутствуют в многочисленных примерах в природе. К ним относятся:

Соты в ульях
Слои пузырьков на поверхности воды имеют форму шестиугольника
Снежинки представляют собой шестиугольную кристаллическую форму льда
Базальтовые колонны
Глаза насекомых

Математика мыльных пузырей и сот

Содержимое

Математика мыльных пузырей
Скопления пузырей в самолете
Пчелиные соты
Мыльные пузыри в космосе
Вопрос недели

Выдувание мыльных пузырей может быть веселым, интересным и увлекательным занятием для всех возрастов. Вы когда-нибудь задумывались, почему мыльные пузыри образуются именно так? Вот простой мыльный пузырь, выдутый из круглой палочки:

Почему мыльный пузырь имеет сферическую форму, а не другую форму, например длинный и тонкий эллипсоид с таким же радиусом, как у круглой палочки? Попробуйте использовать следующую формулу мыла, чтобы выдуть собственные пузыри.

Ингредиенты:
6 частей воды
1 часть жидкости для мытья посуды
Чтобы пузырьки держались дольше, добавьте 1/3 части глицерина или кукурузного сиропа.
Экспериментируйте с различными типами жезлов, такими как ершики для труб, металлические вешалки для одежды или гибкая проволока, согнутая в такие формы, как многоугольники, спирали или сложенные круги.

Что произойдет, если согнуть проволоку в форме круга и опустить ее в мыльную воду? В результате получается мыльная пленка, растянувшаяся по всему кругу. Мыльные пленки принимают форму, которая сводит к минимуму упругую энергию из-за площади поверхности, но при этом охватывает контур палочки. (В физическом мире гравитация также будет играть роль, но пока мы будем игнорировать эти эффекты.)

Когда вы надуваете мыльный пузырь, некоторое количество выдуваемого вами воздуха остается внутри пузыря. Затем мыльный пузырь или группа пузырьков, естественно, пытается минимизировать площадь поверхности для объема (ов), который они заключают, из-за поверхностного натяжения.

Принцип минимальной поверхности : Мыльные пузыри пытаются принять форму наименьшей возможной площади поверхности, содержащей заданный объем.

Математически вопрос о том, какую форму примет мыльный пузырь, представляет собой задачу минимизации: площадь поверхности стремится быть как можно меньше при ограничении (объем постоянен, а граница охватывает заданный контур). Это известно как 93\)? Хотя эта проблема была сформулирована Архимедом, она не была доказана Германом Шварцем до 1884 года в следующей теореме.

Теорема изопериметрии для трех измерений : Фигура с минимальной площадью поверхности для данного объема — это сфера.

Эта теорема показывает, что сфера действительно является трехмерной фигурой, минимизирующей площадь поверхности по всем возможным формам. Поскольку мыльные пузыри пытаются минимизировать площадь поверхности (в отсутствие других физических сил, таких как гравитация), это объясняет, почему мыльные пузыри образуют сферы, а не другие формы.

Что происходит, когда скопления пузырьков собираются вместе? Какие формы они принимают? Подобно одиночным мыльным пузырям, скопления пузырей имеют минимальную форму площади поверхности, которая охватывает несколько областей объема. Давайте сначала рассмотрим, что происходит в двумерной плоскости.

Первое наблюдение заключается в том, что для фиксированных областей \(a_1\) и \(a_2\) два круга, сдвинутые вместе, чтобы разделить общую стену, разделяющую области \(a_1\) и \(a_2\), имеют меньший периметр чем две непересекающиеся окружности.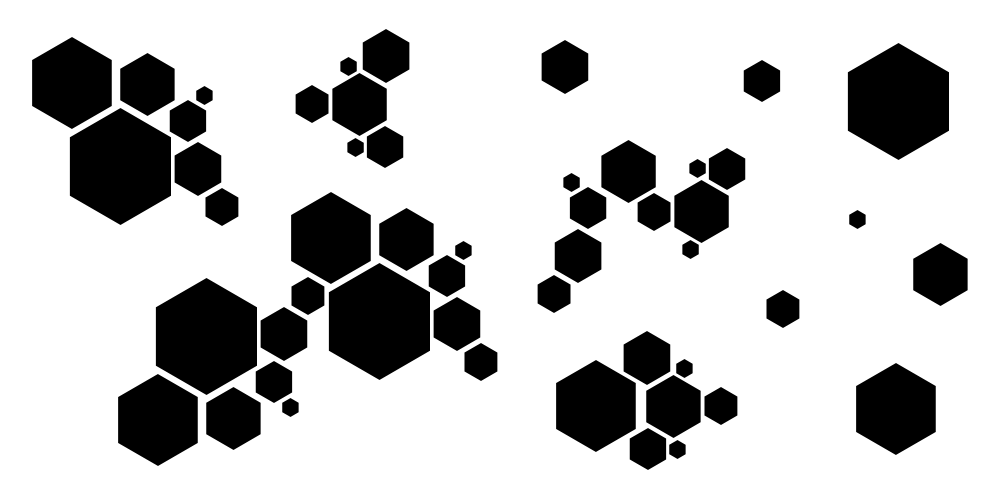 Насколько далеко должны быть сдвинуты эти круги? Дает ли эта фигура минимальный периметр для всех возможных фигур, охватывающих области \(a_1\) и \(a_2\)? Эти вопросы были разрешены следующей теоремой, доказанной в 1993.

Двойной пузырь на плоскости: В 1993 году Альфаро, Брок, Фойзи, Ходжес и Зимба показали, что конфигурация фигур с минимальным периметром, охватывающим две равные площади, достигается для двух пересекающихся окружностей, разделенных линией, так что все дуги пересекаются. под углом 120 градусов:
Красные точки обозначают углы, пересекающиеся под углом 120 градусов.

Тройной пузырь на плоскости: В 2002 году Вичирамала показал, что конфигурация фигур с минимальным периметром, охватывающим три равные площади, достигается для трех пересекающихся окружностей, так что все дуги пересекаются под углом 120 градусов:

Проблема нахождения оптимальных конфигураций с минимальным периметром для четырех и более пузырьков в плоскости в настоящее время остается открытой. Предполагаемая конфигурация фигур следует приведенным выше шаблонам со всеми пересекающимися кругами, встречающимися под углом 120 градусов:

Обычно мыльные пузыри всегда встречаются группами по три под равными углами в 120 градусов. Демонстрация оптимальных конфигураций из четырех или пузырьков все еще остается открытой проблемой — возможно, вы добьетесь успеха в этих предположениях!

Глядя на предполагаемую оптимальную конфигурацию для четырех или более пузырьков в плоскости, возникает следующий вопрос: что произойдет, если мы будем рассматривать все больше и больше пузырьков? Вы можете заметить, что предполагаемая оптимальная конфигурация для большего количества пузырьков начинает напоминать шестиугольную мозаику плоскости. Если эти конфигурации действительно оптимальны, возникает вопрос: наблюдаем ли мы в природе шестиугольные мозаики?

Два примера шестиугольной мозаики в природе:

1) узоры мыльной пленки, образованные между двумя стеклянными пластинами
2) пчелиные соты, которые сделаны из воска и создаются множеством пчел, работающих одновременно в разных частях сот.

В 19 веке Чарльз Дарвин заметил, что соты были инженерным достижением, «абсолютно совершенным в плане экономии труда и воска».

Мы видели, что для одной пчелы, хранящей фиксированное количество меда, форма с наименьшим периметром для хранения фиксированного количества меда — это круг. Однако, если мы упакуем круги бок о бок на плоскости, то эти круги будут оставлять промежутки, а не заполнять все пространство. Другими словами, если несколько пчел работают параллельно, они не будут минимизировать сумму периметров для общего количества запасаемого меда. Вместо этого пчелы нашли решение, которое минимизирует коллектив 9.0104 периметр на общую сумму мед.

Только I и II Только I, II и IV только I, II и III Только I и IV

Многоугольник может замостить плоскость, если конгруэнтные копии многоугольника покрывают плоскость без каких-либо промежутков или перекрытий. Какой из следующих правильных многоугольников может замостить плоскость?

I. Равносторонний треугольник
II. Площадь
III. Обычный Пентагон
IV. Правильный шестиугольник

Исходный файл изображения: Wikimedia Tesellation

Древние греки знали, что периметр, охватывающий фиксированную площадь шестиугольника, меньше периметра квадрата или треугольника той же площади. Однако нет причин, по которым все ячейки должны иметь одинаковую длину сторон, или почему у ячеек не должны быть изогнутые стороны, а не прямые стороны.

Гипотеза сот веками оставалось недоказанным, пока Томас С. Хейлз не представил доказательство в 1999 году.

Теорема о сотах (Хейлза) : Шестиугольная сетка дает лучший способ разделить поверхность на области равной площади с наименьшим общим периметром.

Если плитка имеет изогнутые стороны, то сторона, которая выступает наружу, уменьшает периметр ячейки, а сторона, которая выпирает, вредит периметру. Хейлз доказал, что преимущество выпячивания наружу меньше, чем неудобство выпячивания внутрь. Другими словами, ни одна отдельная ячейка не может работать лучше, чем шестиугольник, если она платит штраф за то, что у нее больше шести сторон, или если она изгибается наружу. Это дало полное доказательство того, что многоугольник с прямыми сторонами работает лучше, чем с изогнутыми сторонами, а шестиугольная мозаика — лучшая из всех конфигураций. Обратите внимание, что в шестиугольной мозаике точки пересечения всегда образуются тройками линий, пересекающихся под углом 120 градусов. См. ниже нашу задачу #why120degrees

Более сложные формы возникают, когда несколько пузырей соединяются в пространстве. Простейшим примером является двойной пузырь, и при объединении трех или более пузырей могут образовываться красивые конфигурации.

Обеспечивает ли эта конфигурация минимальную площадь поверхности для включения и разделения двух разных томов? Как из всех возможных конфигураций доказать, что она лучшая? Этот вопрос долгое время оставался открытым и вызвал множество интересных исследований в области математики под названием 9. 0103 Геометрическая теория меры . В 2000 году Морган, Хатчингс, Риторе и Рос решили эту гипотезу о двойном пузыре для произвольных двойных пузырей.

Теорема о двойном пузыре: Конфигурация, заключающая в себе два фиксированных объема с минимально возможной площадью поверхности, образована двумя пересекающимися сферами, встречающимися под углом 120 градусов на общей окружности.

Если два пузыря в двойном пузыре охватывают один и тот же объем, общая окружность, где встречаются пересекающиеся сферы, является плоской окружностью. Если два пузыря имеют разный объем, то меньший пузырь имеет более высокое внутреннее давление и выпячивается в больший пузырь. Для пузырей любого размера точки встречи всегда образуются тройками пузырей, встречающихся под углом 120 градусов. Это правило 120 градусов всегда выполняется, даже для сложных коллекций пузырьков, таких как пена. Это снова поднимает вопрос #почему120 градусов?

Задача о тройном пузыре все еще широко открыта, и предполагаемая оптимальная конфигурация следует шаблону, приведенному выше, с пересекающимися сферами, встречающимися под углами 120 градусов.

Мыльные пленки между двумя параллельными круглыми кольцами образуют форму катеноида с уравнением \(r = ch(z)\) в цилиндрических координатах.
Катеноид — это минимальная поверхность, все точки которой равны седловые точки , что означает, что в каждой точке изгиб поверхности вверх в одном направлении совпадает с изгибом поверхности вниз в перпендикулярном направлении.
По мере того, как кольца растягиваются дальше друг от друга, шейка будет сужаться до тех пор, пока не будет достигнуто критическое расстояние, а затем катеноид выскочит на два круглых кольца пленки поперек двух параллельных колец. Попробуйте это упражнение сами и поэкспериментируйте, чтобы найти критическую точку разделения!

Для многих больших математических задач поиск решения часто приводит к дополнительным вопросам. Мы изучили принцип минимизации для мыльных пузырей и сот, но возник другой вопрос: почему точки пересечения минимальных поверхностей образованы тройками прямых, пересекающихся под углом 120 градусов? Есть ли у вас интуиция, почему это происходит? Мы рекомендуем вам спросить своих друзей, членов вашей семьи, ваших учителей и обсудить это с другими участниками Brilliant.

About Me

John Cena